对偶问题笔记（1）

发布时间：2023年12月18日

1 从 Lagrange 函数引入对偶问题

考虑如下优化问题 $\begin{align} \begin{cases}\min f_0(x)\\\mathrm{s.t}\quad f_i(x)\leq0,\quad i=1,\cdots,p,\\h_j(x)=0,\quad j=1,\cdots,q,\\x\in\Omega,\end{cases}\end{align}$ 其中 ${f_i\}_{i=0}^p,\:\{h_j\}_{j=1}^q$ 均为定义在 $\mathbb{R}^n$ 取值于 $\overline{\mathbb{R}}$ 上的函数， $\Omega\subset\mathbb{R}^n$ . 设可行集 $\mathcal{D}:=\{x\in\Omega|f_i(x)\leq0,~i=1,\cdots,p;~h_j(x)=0,j=1,\cdots,q\}$ 满足如下条件（该条件是为了后面定义的拉格朗日函数） $\begin{align}\begin{cases}-\infty<f_i(x)\leq\infty&i=0,1,\cdots,p,\\-\infty<h_j(x)<\infty&j=1,\cdots,q,\end{cases}\quad\forall x\in\Omega.\end{align}$ 该问题的 Lagrange 函数定义为
$\begin{aligned}L(x,\lambda,\mu)&:=f_0(x)+\sum_{i=1}^p\lambda_if_i(x)+\sum_{j=1}^q\mu_jh_j(x),\quad(x,\lambda,\mu)\in\Omega\times\mathbb{R}_+^p\times\mathbb{R}^q,\end{aligned}$

其中 $\begin{aligned}\lambda&:=(\lambda_1,...,\lambda_p)^T,\quad\mu:=(\mu_1,...,\mu_q)^T.\end{aligned}$

从正则化的角度来看 Lagrange 函数可以发现 Lagrange 乘子 $\{\lambda_i\}_{i=1}^p$ 和 $\{\mu_j\}_{j=1}^q$ 充当了惩罚项的作用：对任意给定的 $x\in\Omega$ 和 $1\leq i\leq p$ , 如果 $f_i( x) > 0,$ 那么 $\lambda, \mu) \to$ $\infty~(\lambda_i\to\infty)$ .类似地，对任意 $1\leq j\leq q$ ,如果 $h_j(x)\neq0$ , 也有 $L(x,\lambda,\mu)\to\infty~(\mu_j\to$ $\infty$ 或 $-\infty)$ .

所以根据 (2) 有 $\begin{align} &&\sup\limits_{\lambda\succeq0,\mu}L(x,\lambda,\mu)=\begin{cases}f_0(x)&x\in\mathcal{D},\\\infty&x\in\Omega\setminus\mathcal{D},\end{cases}& \end{align}$
从而
$\begin{aligned}\xi^{*}:=\inf_{x\in\mathcal{D}}f_{0}(x)=\inf_{x\in\Omega}\sup_{\lambda\succeq0,\mu}L(x,\lambda,\mu). \end{aligned}$
根据上确界和下确界的性质有：
$\begin{align}\sup_{\lambda\succeq0,\mu}\inf_{x\in\Omega}L(x,\lambda,\mu)\leq\inf_{x\in\Omega}\sup_{\lambda\succeq0,\mu}L(x,\lambda,\mu).\end{align}$ 记 $\begin{aligned}\eta^*:=\sup_{\lambda\succeq0,\mu}g(\lambda,\mu),\end{aligned}$ 其中 $\begin{align}g(\lambda,\mu):=\inf_{x\in\Omega}L(x,\lambda,\mu),\quad(\lambda,\mu)\in\mathbb{R}_+^p\times\mathbb{R}^q.\end{align}$ 则有
$\begin{aligned}\eta^*=\sup_{\lambda\succeq0,\mu}g(\lambda,\mu)\leq\inf_{x\in\mathcal{D}}f_0(x)=\xi^*.\end{aligned}$ 上式给出了优化问题 (1)的最优值 $\xi^*$ 的一个下界，这个下界可以通过求解如下优化问题而得到 $\begin{align}\begin{cases}\max g(\lambda,\mu),\\\mathrm{s.t}\quad\lambda\succeq0&\end{cases}\end{align}$

定义 1.1.1 (对偶函数，对偶问题，对偶性) 我们称(6)为(1)的对偶问题，相对地，称(1)为原问题. (5)所定义的函数 $g(\lambda,\mu)$ 称为 Lagrange 对偶函数，简称为对偶函数，向量 $\lambda,\mu$ 称为对偶变量. 不等式(4), 即 $\eta^*\leq\xi^*$ , 称为问题 (1)的弱对偶性. 若等式 $\eta^*=\xi^*$ 成立，则称问题 (1)满足强对偶性.

命题 1.1.1 (对偶问题是凸的) 由(5)所定义的对偶函数 $g$ 是 $\mathbb{R}_+^p\times\mathbb{R}^q$ 上上半连续的凹函数.

证.对任意固定的 $x\in\mathbb{R}^n$ ,易见 $L(x,\lambda,\mu)$ 是 $\lambda,\mu$ 的仿射函数，因而 $g(\lambda,\mu)$ 是仿射函数的逐点下确界，所以是 $\mathbb{R}_+^p\times\mathbb{R}^q$ 上凹函数.（这是因为有命题：凸函数是仿射函数的逐点上确界）

设 $(\lambda_k,\mu_k)\in\mathbb{R}_+^p\times\mathbb{R}^q$ 满足 $(\lambda_k,\mu_k)\to(\lambda_0,\mu_0)\in\mathbb{R}_+^p\times\mathbb{R}^q$ ,那么， $\forall x\in\Omega$ , 有 $\begin{aligned}g(\lambda_k,\mu_k)\le L(x,\lambda_k,\mu_k)\end{aligned}$ 从而
$\begin{aligned}\lim_{k\to\infty}g(\lambda_k,\mu_k)\le\overline{\lim}_{k\to\infty}L(x,\lambda_k,\mu_k)=L(x,\lambda_0,\mu_0)\end{aligned}$ 由 $x$ 的任意性, 两边对 $x \in ?$ 求下确界, 得 $\operatorname*{\overline{lim}}_{k\to\infty}g(\lambda_k,\mu_k)\leq g(\lambda_0,\mu_0).$ 所以 $g$ 是上半连续的.

注：当
$\begin{align} -\infty<f_i(x),h_j(x)<\infty,\quad\forall x\in\Omega,\quad i=1,...,p;\quad j=1,...,q\end{align}$ 时，Lagrange 函数 $L(x,\lambda,\mu)$ 对所有 $(x,\lambda,\mu)\in\Omega\times\mathbb{R}^p\times\mathbb{R}^q$ 有定义，且对偶函数 $g(\lambda,\mu):=\inf_{x\in\Omega}L(x,\lambda,\mu)$ 对所有 $(\lambda,\mu)\in\mathbb{R}^p\times\mathbb{R}^q$ 有定义. 考察命题 1.1.1的证明可知，此时 $g$ 是定义在 $\mathbb{R}^p\times\mathbb{R}^q$ 的上凹函数.

2. 强对偶性与 KKT 条件

对偶问题可以提供原问题重要的信息. 如上所述, 优化问题(1)恒满足弱对偶性. 它说明对偶问题的最优值 $η^?$ 是原问题的最优值 $ξ^?$ 的一个下界. 实际上在强对偶条件下, 原问题与对偶问题的解满足
一个与 KKT 条件类似但更一般的条件, 它无需目标函数和约束函数的可微性以及点 $x^?$ 的正则性. 当这些函数可微时, 它可以导出 KKT 条件. 从这个视角导出 KKT 条件使得对 Lagrange 乘子有更好的了解, 它们实际上是对偶问题的解.

命题 2.1 设优化问题(1)满足(2), $(x^*,\lambda^*,\mu^*)\in\mathcal{D}\times\mathbb{R}_+^p\times\mathbb{R}^q$ . 那么
$\begin{align} \xi^*=\eta^*,\quad f_0(x^*)=\xi^*,\quad g(\lambda^*,\mu^*)=\eta^*,\end{align}$ 等价于 $\begin{align} \lambda_i^*f_i(x^*)=0,\quad i=1,\cdots,p;\quad L(x^*,\lambda^*,\mu^*)=\inf_{x\in\Omega}L(x,\lambda^*,\mu^*).\end{align}$ 此外，上述任一条成立时，有 $L(x^*,\lambda^*,\mu^*)=\xi^*=\eta^*$ , 且若还存在 $x\in\Omega$ 使得 $f_0(x)<\infty,\quad f_i(x)<\infty,\quad-\infty<h_j(x)<\infty,$ 则 $\xi^*<\infty.$

证. 设(9)成立，则 $\begin{align}\inf_{x\in\mathcal{D}}f_{0}(x)= \xi^*\leq f_0(x^*)=L(x^*,\lambda^*,\mu^*)=\inf_{x\in\Omega}L(x,\lambda^*,\mu^*)=g(\lambda^*,\mu^*)\leq\eta^*\leq\xi^*.\end{align}$ 所以，(8)成立.

反之，设(8)成立，则 $\xi^*=f_0(x^*)\geq L(x^*,\lambda^*,\mu^*)\geq\inf_{x\in\Omega}L(x,\lambda^*,\mu^*)=g(\lambda^*,\mu^*)=\eta^*=\xi^*.$ 所以 $f_0(x^*)=L(x^*,\lambda^*,\mu^*)=g(\lambda^*,\mu^*)$ .第一个等号是(8)给出的条件，以及由 $\lambda^*\succeq0,\quad x^*\in\mathcal{D}$ 可以推导出 (9)的第一式；第二个等号即为(9) 的第二式.

上述条件成立时，有(10)成立，因而 $L(x^*,\lambda^*,\mu^*)=\xi^*=\eta^*$ . 若还存在 $x\in\Omega$ 使得
(9)成立，则利用(8)有， $\xi^*=L(x^*,\lambda^*,\mu^*)\leq L(x,\lambda^*,\mu^*)<\infty.$ 我们称条件 $x^*\in\mathcal{D}$ 为优化问题(1)的可行条件，而称条件(9)为其对偶可行条件，它的关键作用可以从不等式(10)中看出，它确保了强对偶性以及原问题与对偶问题的可解性. 特别，(9)的第一式 “ $\lambda_i^*f_i(x^*)=0,\quad i=1,\cdots,p^*$ 被称为互补松弛条件.

命题 2.2 (强对偶性等价于 KKT 条件) 设优化问题(1)满足(2), $(x^*,\lambda^*,\mu^*)\in$ $\mathbb{R}^n\times\mathbb{R}^p\times\mathbb{R}^q$ .那么， $x^*$ 和 $(\lambda^*,\mu^*)$ 分别是原问题(1)以及对偶问题(6)的解且满足强对偶性 $\xi^*=\eta^*$ 当且仅当 $\begin{align} \begin{cases}x^*\in\mathcal{D},\\\lambda_i^*\geq0,\quad i=1,\cdots,p;\\\lambda_i^*f_i(x^*)=0,\quad i=1,\cdots,p;\\L(x^*,\lambda^*,\mu^*)=\inf_{x\in\Omega}L(x,\lambda^*,\mu^*).\end{cases}\end{align}$ 证. 必要性. $x^*$ 是原问题(1)的解，按照定义可以推出 $x^*\in\mathcal{D}$ 且 $f_0(x^*)=\xi^*;(\lambda^*,\mu^*)$ 是对偶问题(6)的解，同样地按照定义可以推出 $\lambda^*\succeq0$ 且 $g(\lambda^*,\mu^*)=\eta^*;$ 又由于 $\xi^*=\eta^*$ , 所以 $(x^*,\lambda^*,\mu^*)\in$ $\mathcal{D}\times\mathbb{R}_+^p\times\mathbb{R}^q$ 且(8)成立. 显然 $x^*\in\mathcal{D}$ 即为 (11)的第一式成立； $\lambda^*\in\mathbb{R}_+^p$ 蕴含(11)的第二行成立；根据 命题 2.1 可知, $\xi^*=\eta^*,\quad f_0(x^*)=\xi^*,\quad g(\lambda^*,\mu^*)=\eta^*,$ 等价于 $\lambda_i^*f_i(x^*)=0,\quad i=1,\cdots,p;\quad L(x^*,\lambda^*,\mu^*)=\inf_{x\in\Omega}L(x,\lambda^*,\mu^*).$ ，即(11)的最后两行成立.

充分性. 设(11)也就是KKT条件成立，显然由KKT条件的前两行可以推出 $(x^*,\lambda^*,\mu^*)\in\mathcal{D}\times\mathbb{R}_+^p\times\mathbb{R}^q$ ,而KKT条件的后两行即为(9). 由命题 2.1知 (8)与(9)等价，从而有(9)的条件 $\xi^*=\eta^*,\quad f_0(x^*)=\xi^*,\quad g(\lambda^*,\mu^*)=\eta^*$ 成立.

注：当满足KKT条件（或者说满足强对偶性时），条件 $L(x^*,\lambda^*,\mu^*)=\inf_{x\in\Omega}L(x,\lambda^*,\mu^*)$ 可以写成 $L(x^*,\lambda^*,\mu^*)=g(\lambda^*,\mu^*).$

推论 2.3 设优化问题(1)满足 $(2),\quad(\lambda^*,\mu^*)\in\mathbb{R}^p\times\mathbb{R}^q,\quad x^*\in\mathbf{ri}(\Omega)$ ,且 ${f_i\}_{i=0}^p$ 和 ${h_j\}_{j=1}^q$ 均在 $x^*$ 处可微，那么，
$\begin{align} L(x^*,\lambda^*,\mu^*)=\inf_{x\in\Omega}L(x,\lambda^*,\mu^*)\end{align}$ 蕴含 $\begin{align}\nabla_xL(x^*,\lambda^*,\mu^*)\perp V_\Omega.\end{align}$ 并且当优化问题(1)是凸问题时，二者等价.

证. 由于 $x^*\in\mathbf{ri}(\Omega)$ , 利用优化问题笔记中的 命题 1.2.1 可知 (12)能够推导出(13). 特别地当优化问题(1)是凸问题时，由于 $L(x,\lambda^*,\mu^*)$ 关于 $x$ 为凸函数，由优化问题笔记中的命题 3.1.2 可知 $x^*$ 是 $(f,\mathcal{D})$ 的一个全局最优解当且仅当 $\nabla f(x^*)^T(x-x^*)\ge0,\quad\forall x\in\mathcal{D}$ ，(12)等价于
$\nabla_xL(x^*,\lambda^*,\mu^*)^T(x-x^*)\geq0,\quad\forall x\in\Omega.$ 由于 $x^*\in\mathbf{ri}(\Omega)$ ,根据优化问题中的引理 1.2.2可知此条件等价于 (13).

命题 2.2 说明当优化问题(1) 满足强对偶性, 且原问题和对偶问题均可解时, 可以按一定的步骤求解其最优解 $x^*$ :

算法 2.1 优化问题(1)的求解算法：
(2.1.1) 计算对偶函数 $g(\lambda,\mu)$ ;
(2.1.2) 求解对偶问题(6), 得解 $(\lambda^*,\mu^*)\in\mathbb{R}_+^p\times\mathbb{R}^q;$
(2.1.3) 求解 $L(x^*,\lambda^*,\mu^*)=g(\lambda^*,\mu^*)$ ,得解 $x^*;$
(2.1.4) 检验 $x^*$ 是否对偶可行条件的第一项：
$\begin{align} x^*\in\mathcal{D},\quad\lambda_i^*f_i(x^*)=0,\quad i=1,\cdots,p.\end{align}$

注：根据对偶函数 $g(\lambda,\mu)$ 的定义可知，步骤 (2.1.) 等价于求解优化问题
$x^*=\operatorname*{argmin}_{x\in\Omega}L(x,\lambda^*,\mu^*).$ 一旦 算法 2.1 能执行完成，并使所求得的 $x^*$ 以及 $(\lambda^*,\mu^*)$ 满足(14), 那么，根据 命题 2.2, $x^*$ 和 $(\lambda^*,\mu^*)$ 必是优化问题(1)及其对偶问题 (6)的解，且满足强对偶性.

3. 对偶性的鞍点特征

在这小节中将说明强对偶性的几何表现。

首先，强对偶性 $\eta^*=\xi^*$ , 即 $\begin{align} \sup_{\lambda\succeq0,\mu\in\mathbb{R}^q}\inf_{x\in\Omega}L(x,\lambda,\mu)=\inf_{x\in\Omega}\sup_{\lambda\succeq0,\mu\in\mathbb{R}^q}L(x,\lambda,\mu)\end{align}$ 中，拉格朗日函数 $L(x,\lambda,\mu)$ 可以看成由两部分所组成： $(x)$ 和 $(\lambda,\mu)$ ，更为一般地，考虑多元函数 $f (x, y)$ 以及类似于(15)的等式： $\begin{align}\sup_{y\in B}\inf_{x\in A}f(x,y)=\inf_{x\in A}\sup_{y\in B}f(x,y)\end{align}$ 其中有效定义域为 $\begin{aligned}\textbf{dom}(f)=A\times B\subset\mathbb{R}^n\times\mathbb{R}^m\end{aligned}$ ，记 $\begin{align}\xi^*:=\inf_{x\in A}\sup_{y\in B}f(x,y),\quad\eta^*=\sup_{y\in B}\inf_{x\in A}f(x,y).\end{align}$

命题 3.1 (极大极小不等式) 给定函数 $f:A\times B\to\overline{\mathbb{R}}$ ,其中 $A\subset\mathbb{R}^n,~B\subset\mathbb{R}^m$ 均为非空子集，有 $\eta^*\leq\xi^*.$

证. 对任意的 $x\in A,\:y\in B$ ,根据确界的定义，有 $\inf_{x\in A}f(x,y)\leq f(x,y)$ .两边对 $y\in B$ 求上确界，得
$\sup\limits_{y\in B}\inf\limits_{x\in A}f(x,y)\leq\sup\limits_{y\in B}f(x,y).$ 两边再对 $x\in A$ 求下确界即得 $\eta^*\leq\xi^*.$

类似于Larange 对偶函数的情况，称 $\eta^*\leq\xi^*.$ 为弱对偶性，称 $\eta^*=\xi^*.$ 为强对偶性.

若(16)左边的上确界能达到，那么，存在 $y^*\in B$ , 使得 $\begin{aligned}\eta^*=\inf_{x\in A}f(x,y^*)=\sup_{y\in B}\inf_{x\in A}f(x,y).\end{aligned}$ 同理，对于(16)式右边的下确界，若可以达到，则存在 $x^*\in A$ , 使得 $\begin{aligned}\xi^*=\sup_{y\in B}f(x^*,y)=\inf_{x\in A}\sup_{y\in B}f(x,y).\end{aligned}$ 所以，当(16)成立的时候，也就是 $\xi^* = \eta^*$ ，则有： $\sup_{y\in B}f(x^*,y)=\xi^*=\eta^*=\inf_{x\in A}f(x,y^*).$ 从而
$\begin{aligned}f(x^*,y)\leq\sup\limits_{y\in B}f(x^*,y)=\xi^*=\eta^*=\inf\limits_{x\in A}f(x,y^*)\leq f(x,y^*),\quad\forall x\in A,\:y\in B.\end{aligned}$ 上式中取 $x=x^*,\:y=y^*$ , 可以得到 $f(x^*,y^*)=\xi^*=\eta^*$ . 所以
$\begin{align} f(x^*,y)\leq f(x^*,y^*)\leq f(x,y^*),\quad\forall x\in A,\:y\in B.\end{align}$ 这说明 $x^*,y^*)$ 是 $f$ 中的鞍点，定义如下.

定义 3.1 (鞍点) 对于函数 $f:A\times B\to\overline{\mathbb{R}}$ ,其中 $A\subset\mathbb{R}^n,\quad B\subset\mathbb{R}^m$ ,若 $(x^*,y^*)\in A\times B$ 满足(18),则称之为 $f$ 的一个鞍点.

图 3.1：鞍点示意图

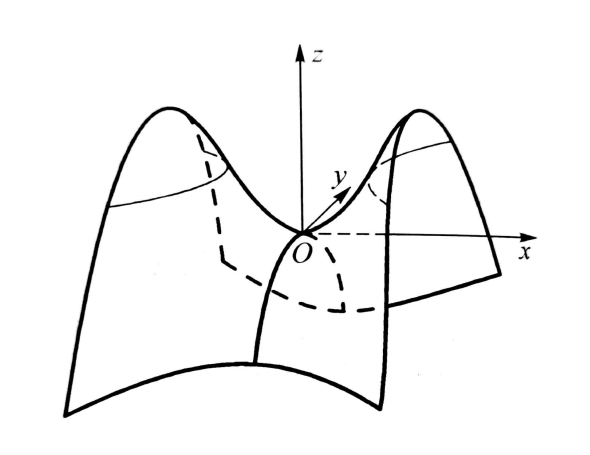
命题 3.2 (强对偶性的鞍点刻画) 给定函数 $f:A\times B\to\overline{\mathbb{R}}$ ,其中 $A\subset\mathbb{R}^n,~B\subset\mathbb{R}^m$ , $(x^*,y^*)\in A\times B$ 是 $f$ 的一个鞍点，即满足(18), 当且仅当 $\begin{align} \sup\limits_{y\in B}f(x^*,y)=\xi^*=\eta^*=\inf\limits_{x\in A}f(x,y^*).\end{align}$ 此外，当 $x^*,y^*)$ 是 $f$ 的鞍点时，有 $x^* , y^* ) = \xi^* .$

证.充分性如上已证，下证必要性.

设 $x^*,y^*)$ 是 $f$ 的一个鞍点，则(18)式成立，即 $f(x^*,y)\leq f(x^*,y^*)\leq f(x,y^*),\quad\forall x\in A,\:y\in B$ ，这个式子的第一个不等式对 $\in B$ 求上确界，第而个不等式对 $\in A$ 求下确界，可以得到 $\begin{align}\sup_{y\in B}f(x^*,y)\leq f(x^*,y^*)\leq\inf_{x\in A}f(x,y^*).\end{align}$ 从而有 $\begin{aligned}\xi^*&=\inf_{x\in A}\sup_{y\in B}f(x,y)\le\sup_{y\in B}f(x^*,y)\le f(x^*,y^*)\le\inf_{x\in A}f(x,y^*)\le\sup_{y\in B}\inf_{x\in A}f(x,y)=\eta^*.\end{aligned}$

如果我们将鞍点的定义用到优化问题(1)的拉格朗日函数中去，会发生什么呢？设 $g(\lambda,\mu)$ 是优化问题(1)的对偶函数，而 $\xi^*$ 和 $\eta^*$ 分别是优化问题(1)及其对偶问题的最优解，我们称解 $(x^*,\lambda^*,\mu^*)$ 为拉格朗日函数 $L(x,\lambda,\mu)$ 的鞍点，如果满足条件： $L(x^*,\lambda,\mu)\leq L(x^*,\lambda^*,\mu^*)\leq L(x,\lambda^*,\mu^*),\quad\forall x\in\Omega,(\lambda,\mu)\in\mathbb{R}_+^p\times\mathbb{R}^q.$ 于是，这就可以说明鞍点是可以用来刻画优化问题(1)及其对偶问题(6)的解以及强对偶性.

文章来源:https://blog.csdn.net/weixin_47255403/article/details/135067432
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！

对偶问题笔记（1）

目录

1 从 Lagrange 函数引入对偶问题

2. 强对偶性与 KKT 条件

3. 对偶性的鞍点特征