平面光波导_三层均匀平面光波导_射线分析法

平面光波导_三层均匀平面光波导_射线分析法

三层均匀平面光波导：

• 折射率沿 $x$ 方向有变化，沿 $y$、$z$ 方向没有变化
• 三层：芯区($n_1$) $>$ 衬底($n_2$) $\ge$ 包层($n_3$)
• 包层通常为空气，即 $n_3=1$；芯区与衬底折射率之差通常为 $10^{?3}～10^{?1}$；芯区一般几微米厚

一、三层均匀平面波导的射线分析法

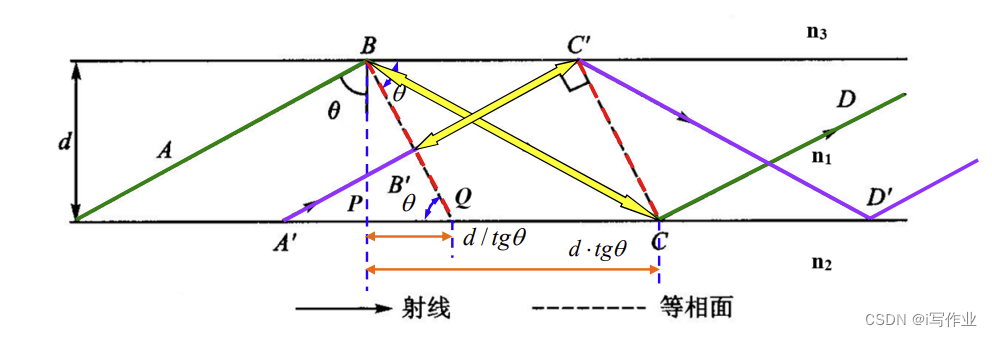
三层均匀平面波导的传输路线（也是叠加模型）如上图所示：

• 它可以看作由斜着向上界面行进的平面波（以 $B{B}^{\prime }$ 为等相位面的平面波），与反射2次后再次斜向上运动的平面波（以 $C{C}^{\prime }$ 为等相位面的平面波）相互叠加而成
• 入射光满足全反射条件仅仅能使光被约束在波导中，是形成导波的必要条件（还有是否可以传输）
• 因为导波由2个平面波相叠加，所以当两平面波到达同一地点时，只有满足相位相同的条件，才会相干相长，维持光在波导中传播。否则会相互抵消，导致无法传播

传输条件——相干叠加条件的推导：

约束条件：$AB?A^{\prime }{B}^{\prime }$ 平面波（以 $B{B}^{\prime }$ 为等相位面的平面电磁波）向前传播，第一个发生第二次反射的点（$C$ 点）其发生全反射相移后仍应与前一入射平面波保持同相。

记全反射在两界面带来的相移分别为：$?2{?}_{12}$、$?2{?}_{13}$

因为 $B{B}^{\prime }$、$C{C}^{\prime }$ 是等相位面，需要 $AB{A}^{\prime }{B}^{\prime }$ 平面波与 $CD{C}^{\prime }{D}^{\prime }$ 平面波相干相长，因此计算 $B^{\prime }{C}^{\prime }$ 和 $BC$ 分别带来的光程，且两光程差应为 $2\pi$ 的整数倍

其中入射光的初始状况、三层均匀平面波导的各层折射率、波导芯区厚度是易于获取的参数，各表达式最终应当尽可能使用这三类参数表达

• $B^{\prime }\to C^{\prime }$ 的光程：$n_1\overline{B^{\prime }{C}^{\prime }}=n_1\overline{B{C}^{\prime }}\sin \theta =n_1(\overline{PC}?\overline{PQ})\sin \theta =n_1\left(d\tan \theta ?d/\tan \theta \right)\sin \theta$

  其总相移为：$k_0{n}_1\left(d\tan \theta ?d/\tan \theta \right)\sin \theta$

• $B\to C$ 的光程：$n_1\overline{BC}=n_1?d/\cos \theta$

  其在界面 1,2 和界面 1,3 分别发生了一次全反射，带来的相移为 $?2{?}_{12}?2{?}_{13}$

  其总相移为：$k_0{n}_1?d/\cos \theta ?2{?}_{12}?2{?}_{13}$

此时两平面波相干相长即要求：
$$k_0{n}_1?d/\cos \theta ?2{?}_{12}?2{?}_{13}?k_0{n}_1\left(d\tan \theta ?d/\tan \theta \right)\sin \theta =2m\pi m=0,1,2,?$$

此式只与三层平面均匀波导的厚度、折射率，入射光的入射角、波数有关；其分立的解对应导波的不同模式

将上式简记为：
$$\kappa d=m\pi +{?}_{12}+{?}_{13}\text{\hspace{1em}(模式的本征方程/特征方程)}$$

• $\kappa =k_x=n_1{k}_0\cos \theta =\sqrt{n_1^2{k}_0^2?{\beta }^2}=k_0\sqrt{n_1^2?N^2}$

• 模折射率/有效折射率：$N=\beta /k_0$

• $\beta$ 为传播常数。通过模式的本征方程/特征方程可以求出不同模式的传播常数

---

对于 TE、TM，其全反射相移公式为：
$$r_{TE}=\frac{{\vec{E}}_0^{\prime }}{{\vec{E}}_0}=\frac{n_1\cos {\theta }_1?\sqrt{n_2^2?n_1^{2}si{n}^2{\theta }_1}}{n_1\cos {\theta }_1+\sqrt{n_2^2?n_1^{2}si{n}^2{\theta }_1}}=exp\left[?j2\arctan \left(\frac{\sqrt{n_1^2{\sin }^2{\theta }_1?n_2^2}}{n_1\cos {\theta }_1}\right)\right]=e^{?j2{?}_{TE}}$$

$$r_{TM}=\frac{{\vec{H}}_0^{\prime }}{{\vec{H}}_0}=\frac{n_2^2\cos {\theta }_1?n_1\sqrt{n_2^2?n_1^{2}si{n}^2{\theta }_1}}{n_2^2\cos {\theta }_1+n_1\sqrt{n_2^2?n_1^{2}si{n}^2{\theta }_1}}=exp\left[?j2\arctan \left(\frac{n_1^2}{n_2^2}\frac{\sqrt{n_1^2{\sin }^2{\theta }_1?n_2^2}}{n_1\cos {\theta }_1}\right)\right]=e^{?j2{?}_{TM}}$$

可以简记为：
$$\begin{gathered} TEmode?\begin{array}{l}{?}_{12}=\arctan \left(\frac{P}{\kappa }\right)\\ \\ {?}_{13}=\arctan \left(\frac{q}{\kappa }\right)\end{array} \\ TMmode?\begin{array}{l}{?}_{12}=\arctan \left(\frac{n_1^2}{n_2^2}\frac{P}{\kappa }\right)\\ \\ {?}_{13}=\arctan \left(\frac{n_1^2}{n_3^2}\frac{q}{\kappa }\right)\end{array} \end{gathered}$$
其本征方程为：
$$\begin{gathered} TE:\kappa d=m\pi +\arctan \left(\frac{P}{\kappa }\right)+\arctan \left(\frac{q}{\kappa }\right) \\ TM:\kappa d=m\pi +\arctan \left(\frac{n_1^2}{n_2^2}\frac{P}{\kappa }\right)+\arctan \left(\frac{n_1^2}{n_3^2}\frac{q}{\kappa }\right) \end{gathered}$$