权重初始化和激活函数小结

本文章参考李沐老师的动手深度学习,作为个人的笔记.

4.8. 数值稳定性和模型初始化 — 动手学深度学习 2.0.0 documentation (d2l.ai)

前言

首先我们理想的神经网络是什么样子的?

一.权重初始化

二.检查激活函数

总结

---

前言

选择合理的权重初始化和选择合理的激活函数在训练是保证训练的稳定性尤为重要,本文介绍其做法,帮助我们事半功倍.

首先我们理想的神经网络是什么样子的?

这样的一个神经网络对于我们来说才是很好的,并且我们要达到这样的要求我们要做什么呢?

一.权重初始化

• 在合理值区间例随机初始参数.
• 训练开始得时候更容易有数值不稳定.

1. 远离最优解的地方损失函数的表面可能很复杂.
2. 最优解附近表面会比较平

• 使用N(0,0.01)来初始可能对小网络没有问题,但不能保证深度神经网络.

这里放一个图帮助大家理解.

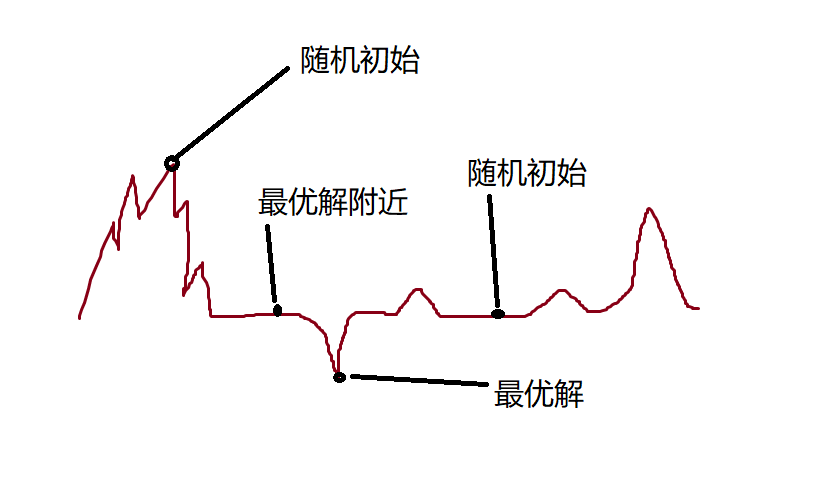
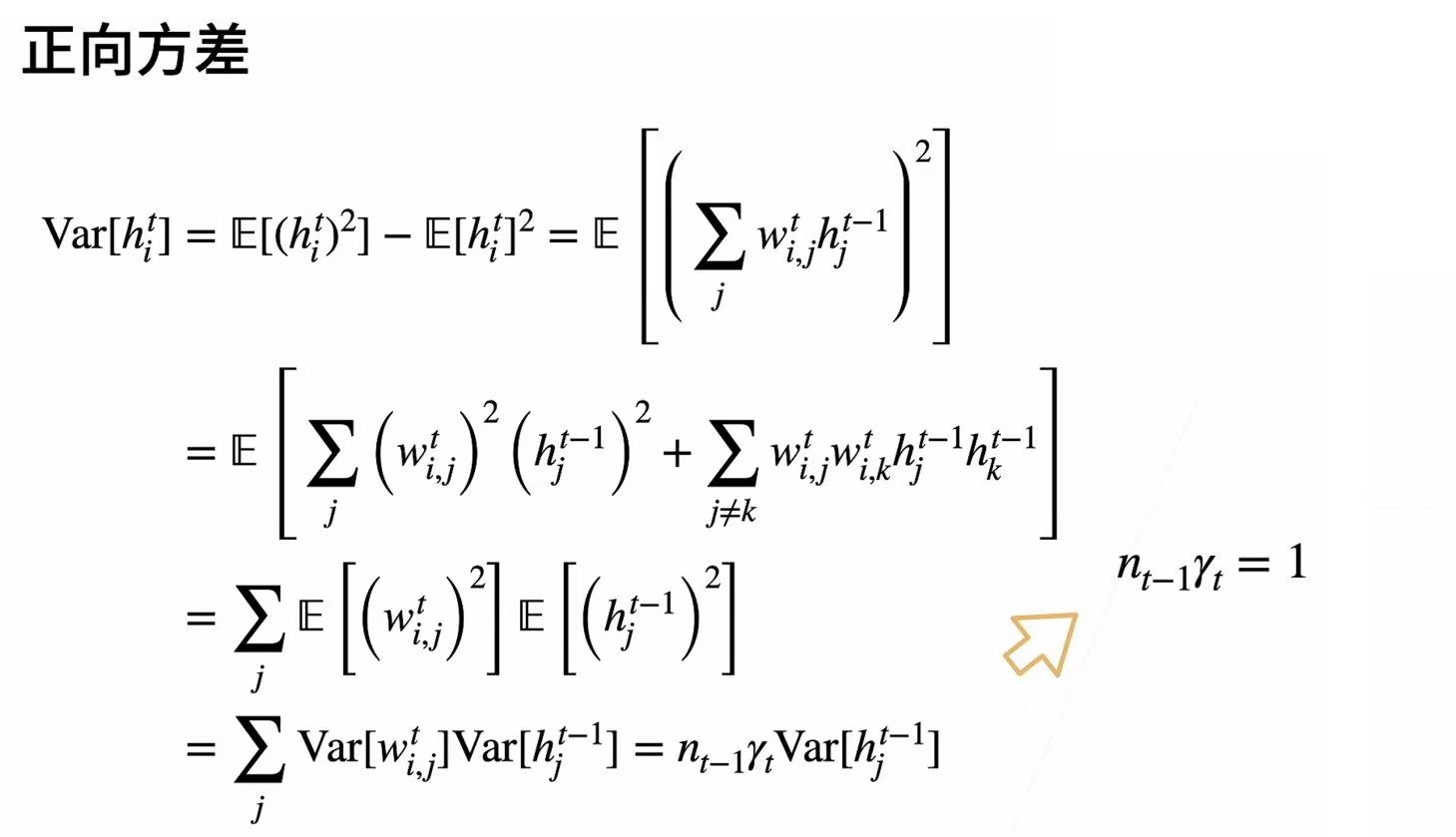
二.检查激活函数

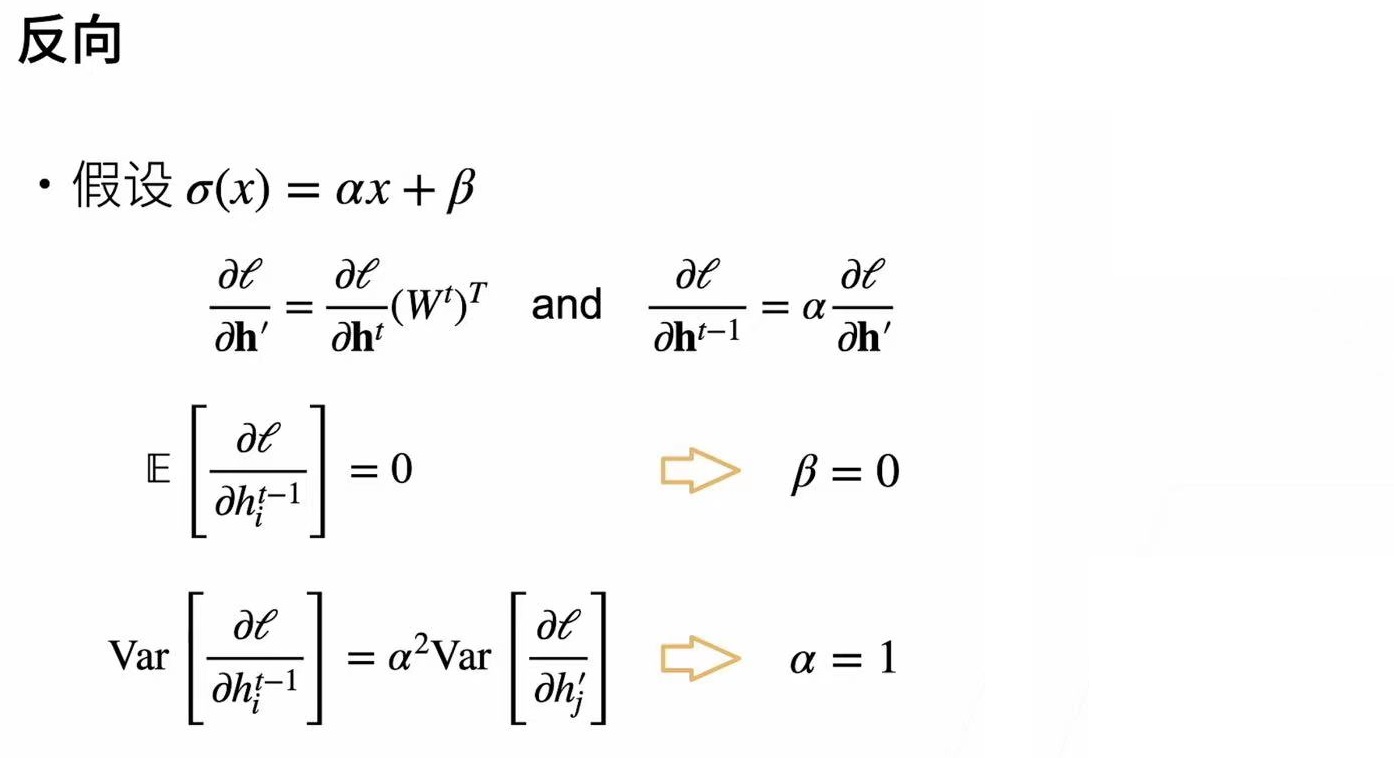
上述公式表明我们的激活函数必须是f(x) = x 在零附近可以近似的看作是f(x) = x,而且神经网络的权重通常是在零点附近比较小的数,所以tanh(x)与relu(x)是可以满足我们要求的,而sigmoid函数不满足,但可以进行平移变换来将函数调整.

---

总结

• 梯度消失和梯度爆炸是深度网络中常见的问题。在参数初始化时需要非常小心，以确保梯度和参数可以得到很好的控制。

• 需要用启发式的初始化方法来确保初始梯度既不太大也不太小。

• ReLU激活函数缓解了梯度消失问题，这样可以加速收敛。

• 随机初始化是保证在进行优化前打破对称性的关键。

• Xavier初始化表明，对于每一层，输出的方差不受输入数量的影响，任何梯度的方差不受输出数量的影响。