力扣日记1.11-【二叉树篇】450. 删除二叉搜索树中的节点
发布时间:2024年01月11日
力扣日记:【二叉树篇】450. 删除二叉搜索树中的节点
日期:2024.1.11
参考:代码随想录、力扣
450. 删除二叉搜索树中的节点
题目描述
难度:中等
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:
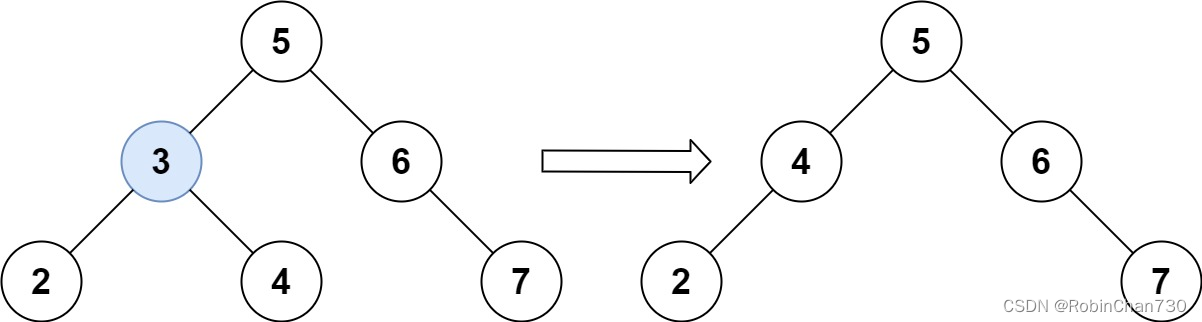
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如上图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
提示:
- 节点数的范围 [0, 10^4].
- -10^5 <= Node.val <= 10^5
- 节点值唯一
- root 是合法的二叉搜索树
- -10^5 <= key <= 10^5
进阶: 要求算法时间复杂度为 O(h),h 为树的高度。
题解
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
#define SOLUTION 1
public:
#if SOLUTION == 1
TreeNode* deleteNode(TreeNode* root, int key) {
// 空树直接返回(或者找到底也没找到key)
if (root == nullptr) return root;
// 找到了,开始删除
if (root->val == key) {
// 如果左节点为空,直接返回右节点
if (root->left == nullptr) return root->right; // 右节点可能为空可能不为空
// 如果右节点为空,直接返回左节点
else if (root->right == nullptr) return root->left; // 左节点不为空
// 这里则是左右节点都不为空
else {
// 如果root的左节点没有右子节点,可以把右子树直接作为左节点的右子树
if (root->left->right == nullptr) {
root->left->right = root->right;
return root->left; // 返回root的左节点作为新的根节点
}
// 如果root左节点存在右子节点,则看root的右节点的左子节点
else if (root->right->left == nullptr) {
root->right->left = root->left;
return root->right; // 返回root的右节点作为新的根节点
}
else {
// 这里则是root的左节点有右子节点,且右节点有左子节点
// 把root右子树接到root左子树中
// 循环找到root的左节点的右子节点为空(最右节点的值是最大的)
TreeNode* cur = root->left;
while (cur->right != nullptr) {
cur = cur->right;
}
// 此时cur->right为空
cur->right = root->right;
return root->left; // 把root的左节点返回
}
}
}
// 没找到,看大小,继续递归
if (key > root->val) { // 往右找
root->right = deleteNode(root->right, key); // 找到会返回新的右子树根节点
} else { // 另一种情况就是往左找
root->left = deleteNode(root->left, key); //
}
return root;
}
#endif
};
复杂度
时间复杂度:
空间复杂度:
思路总结
- 能解出题来好开心(/(ㄒoㄒ)/~~,虽然过程和代码写的很不简洁,但太难得了(悲
- 注释的过程即为解题思路过程,可以多画点图模拟一下
- 关于找到key后删除当前root节点的思路,分几种情况:
-
- 如果root左节点为空,直接返回右节点
-
- 如果root右节点为空,直接返回左节点
-
- 如果左右节点都不为空
- 1)首先:考虑 如果root的左节点没有右子节点,可以把右子树直接作为左节点的右子树
- 2)如果root左节点存在右子节点,则看root的右节点的左子节点,思路同理
- 3)如果都不满足,即root的左节点有右子节点,且右节点有左子节点
- 则考虑把root右子树接到root左子树中
- 通过 不断迭代 root的左子树中的右子节点,直到找到 右子节点为空(因为最最右的右子节点的值是左子树中最大的)
- 找到后,把root的右子节点接到该空节点处,并返回root的左节点
-
- 关于删除后返回节点或者递归接收节点的思路:与插入是类似的,都是假定递归函数返回操作(如这里的删除以及上一题的插入)后的新子树根节点,作为当前root节点的新子节点。
- 如果还未找到key,则可根据二叉搜索树的性质,根据key的大小往左或往右递归寻找,直到递归到空节点则直接返回nullptr。
- 改进:实际上,对于删除节点时root左右节点都不为空的情况(即第3点),可以都作为第三种情况来考虑(即第3)点),即直接考虑将root右子树接到root左子树中(左子树的右子节点为空则直接接到该空节点处即可,否则就进行迭代找到空右子节点)
文章来源:https://blog.csdn.net/weixin_45847708/article/details/135538365
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- SoniTranslate
- [代码随想录1]头文件的符号命名
- 浅谈拨测在网络安全中的应用
- 微电网优化MATLAB:蚁群算法(Ant Colony Optimization,ACO)求解微电网优化(提供MATLAB代码)
- 【微信小游戏可视化实战】飞机大战
- HttpRunner辅助函数debugtalk.py
- 系统学Prompt,强烈推荐这3个教程,OpenAI还是最强
- Qt 6.3 学习笔记
- Vue2【插槽】
- 接雨水【双指针】【前缀后缀】