深度神经网络结构
单层的感知机不能解决“异或”问题。

- 在前面分别介绍了M-P神经元模型和感知机模型。在M-P神经元模型中,神经元接收到若干个输入信号,并将计算得到的加权后的总输入,经过激活函数的处理,最终产生神经元的输出。而感知机模型则由两层神经元组成,输入层接收外界输入信号后,经过激活函数处理,传递给输出层,输出层再经过激活函数处理形成最终的输出。
- 还讲到,单层的感知机不能解决“异或”问题,也正是因此被人工智能泰斗明斯基并无恶意地把人工智能打入“冷宫”二十载。其实解决“异或”问题的关键在于能否解决非线性可分问题,而要解决非线性问题就需要提高网络的表征能力,也就是需要使用更加复杂的网络。
按照这个思路,我们可以考虑在输入层和输出层之间添加一层神经元,将其称之为隐藏层(Hidden Layer,又称“隐含层”或“隐层”)。
- 多层感知机模型?— 在输入层和输出层之间添加一层神经元,将其称之为隐藏层(Hidden Layer)这样一来输入与隐藏单元,隐藏单元与输出单元之间,都有了权重相连,也就是说这个模型是全连接的,并且隐藏层和输出层中的神经元都拥有激活函数。
- 这样一来输入与隐藏单元,隐藏单元与输出单元之间,都有了权重相连,也就是说这个模型是全连接的,并且隐藏层和输出层中的神经元都拥有激活函数。这种多层感知机模型,就能够解决单个神经元无法解决的异或问题了,如当权重[𝑤_1,𝑤_2,𝑤_3,𝑤_4,𝑤_5,𝑤_6] =[1,-1,-1,1,1,1],各个神经元阈值𝜃均为0.5时,可以实现“异或”功能。
神经网络模型
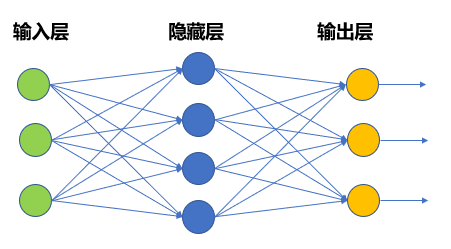
- 虽然多层感知机模型较M-P神经元而言已经有了很大进步,但这一类模型仍然无法很好地解决比较复杂的非线性问题。因此,在多层感知机模型的基础上,还研究出了如图所示的神经网络模型。
- 神经网络模型具有如下特点:
- 由输入层、隐藏层和输出层组成,根据问题的需要,结构中可能含有更多隐藏层;
- 每层神经元与下一层神经元两两之间建立连接;
- 神经元之间不存在同层连接,也不存在跨层连接;
- 输入层仅仅起到接收输入的作用,不进行函数处理;
- 而隐藏层与输出层的神经元都具有激活函数,是功能神经元。上图所示为具备单个隐藏层的神经网络。
深度神经网络(Deep Neural Network,DNN)— 将若干个单层神经网络级联在一起,前一层的输出作为后一层的输入。

- 此外,针对以上的第1条中,对于神经网络模型,当隐藏层如下图中所示大于等于两层时,就称之为深度神经网络(Deep Neural Network,DNN)。
- 在这种结构中,将若干个单层神经网络级联在一起,前一层的输出作为后一层的输入,这样构成了多层前馈神经网络(Multi-layer Feedforward Neural Networks)更确切地说,每一层神经元仅与下一层的神经元全连接,并且输入层—隐藏层、隐藏层—隐藏层、隐藏层—输出层之间,都有权重相连。但在同一层之内,神经元彼此不连接,而且跨层之间的神经元,彼此也不相连。
- 之所以加上“前馈”这个定语,是想特别强调,这样的网络是没有反馈的。也就是说,位置靠后的层次不会把输出反向连接到之前的层次上作为输入,输入信号可以“一马平川”地单向向前传播。很明显,相比于纵横交错的人类大脑神经元的连接结构,这种结构做了极大简化,即使如此,它也具有很强的表达力。
- 在上图的DNN模型中,输入从最左侧的输入单元进入DNN模型,从左至右依次经过两个隐藏层,最后到达输出层形成输出。每一次层间的传递,都是加权求和的过程。在到达下一层后,会经过激活函数的作用,成为这一层的输出。站在数学的角度看,其实权重作用,就是对上一层的输出进行线性变换,作为下一层的输入。激活函数的作用则是对输入进行了非线性的映射。在深度网络的结构下,权重和激活函数结合,使得模型具备了解决复杂的线性不可分问题的能力。
4.2 深度神经网络的训练过程
4.2.1 基本概念
深度神经网络模型解决回归问题。

- 从左至右用𝑤,𝑤^′,𝑤^′′来标记这三个矩阵(偏置𝜃假设全为零)。矩阵的维度是由相邻两层神经元的个数决定的。对于全连接网络,权重矩阵的维度应该为𝑛(𝑡+1)?𝑛(𝑡),即后一层的神经元数量乘本层的神经元数量。输入的维度是21, 维度是32,𝑤^′维度是33,𝑤^′′维度是23。为了方便讲解,在本案例中三个权重矩阵初始值如图中公式
- 隐藏层单元和输出层单元都具有激活函数,在这里使用sigmoid(𝑓(𝑥)=1/(1+𝑒^(?𝑥) ))函数。虽然实际应用中都是用大量的数据进行训练的,在这里先用一条数据来进行讲解,输入值为0.2、0.5,真值为0.3、0.8。由于最终的真值是数值,因此这是一个回归问题。
前向传播 — 从输入层出发,逐层推进,将上一层的输出与权重结合后,作为下一层的输入,并计算下一层的输出,如此进行,直到运算到输出层为止。

- 此案例中,输入经过权重𝑤和激活函数𝑓后,得到第一个隐藏层的输出,是一个3*1的向量,分别是(𝑓为sigmoid函数):
𝑓(0.2×(?0.43)+0.5×(?0.37))=0.43
𝑓(0.2×0.04+0.5×0.40)=0.55
𝑓(0.2×0.04+0.5×0.40)=0.55
- 这个向量,经过 后作为输入,带入sigmoid函数,得到了第二个隐藏层的输出。这个输出依然是3*1的向量:
𝑓(0."43"×(?0."51")+0."55"×(?0.35)+"0.48"×"0.26"))=0.43
𝑓(0."43"×(?0."34")+0."55"×(?0."44")+"0.48"×"0.28")=0.44
𝑓(0."43"×"0.55"+0."55"×(?0.31)+"0.48"×"0.06")=0."53"
- 最后,这个向量经过 作为输入,经过sigmoid,得到最终输出,计算后是:
𝑓(0."43"×"0.36"+0."44"×(?0.30)+"0.53"×"0.24")=0."54"
𝑓(0."43"×"0.27"+0."44"×"0.35"+"0.53"×(?"0.31"))=0."53"
计算损失 — 利用损失函数来调节网络中的权重,进而减小损失函数,即使得输入经过权重能准确的预测出实际值。

-
计算损失,在机器学习中的“有监督学习”算法里,在假设空间𝛤中,构造一个决策函数𝑓, 对于给定的输入𝑥,由𝑓(𝑥)给出相应的输出 ,这个实际输出值ˉ𝑌和原先预期值𝑌可能不一致。于是,需要定义了一个损失函数(Loss Function),也有人称之为代价函数(Cost Function)来度量两者之间的“落差”程度。这个损失函数通常记作𝐿(𝑌,𝑌??)=𝐿(𝑌,𝑓(𝑋)),为了方便起见,这个函数的值为非负数。损失函数值越小,说明实际输出ˉ𝑌和预期输出𝑌之间的差值就越小,也就说明构建的模型越好。因此神经网络学习的本质,其实就是利用损失函数来调节网络中的权重,进而减小损失函数,即使得输入经过权重能准确的预测出实际值。
-
对于不同类型的问题,通常会使用不同的损失函数。比如对于回归问题,一般会使用均方差损失MSE,或平均绝对误差损失MAE。均方差损失和平均绝对误差损失的计算公式如下方所示,𝑦_𝑖为维度𝑖的真值,𝑦??_𝑖为预测值,也就是输出。MSE计算的是每一项误差的平方,而MAE计算的是每一项误差的绝对值。𝑀𝑆𝐸=1/𝑛 ∑2_(𝑖=1)^𝑛?(𝑦_𝑖?𝑦??_𝑖 )^2 、𝑀𝐴𝐸=1/𝑛 ∑_(𝑖=1)^𝑛?|𝑦_𝑖?𝑦??_𝑖 |
-
对于分类问题,MSE和MAE也是可用的,但更多情况下,使用的是交叉熵损失函数。确切地说,是将Softmax激活函数和交叉熵损失CrossEntropy搭配使用,交叉熵函数表达式如图中"CrossEntropy"所示。这一点,我们在后续会进行讲解。
-
此处,使用MSE来作为损失函数来计算损失。在前向传播中通过给定的权重计算出的实际输出为0.54和0.53,因此总的损失应该是(0.3-0.54)的平方加上(0.8-0.53)的平方,再除以2,计算的到的结果是 0.066,即为我们在这一次前向传播过程中预测值与真值的偏差。
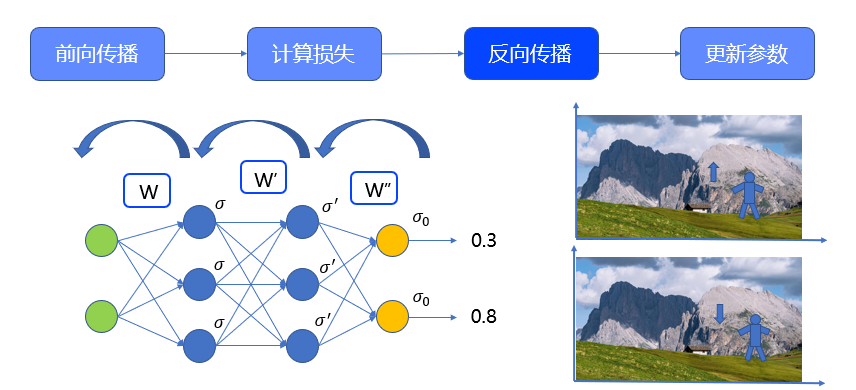
反向传播——沿着模型相反的方向,从后向前地逐层计算每个神经元的损失,并更新参数。
-
反向传播,所谓反向传播,就是沿着模型相反的方向,从后向前地逐层计算每个神经元的损失,并更新参数。以神经网络为例,从输出层出发,首先被更新的,应该是输出层与第二个隐藏层之间的权重矩阵 ,第二被更新的,是两个隐藏层之间的权重矩阵𝑤^′,最后被更新的是输入层和第一个隐藏层的权重矩阵𝑤,示意图如图所示。
-
在训练中,反向传播需要搭配优化算法才能实现参数的更新。接下来就来介绍一个经典优化策略——梯度下降。
-
我们训练的最终目标就是让损失函数的值最小,因为当损失函数值最小的时候,预测值最接近真值。当然最理想的情况是损失为零,此时预测值与真值完全相符。由于模型复杂,所以无法知道损失函数的全貌,那我们要怎么决定向哪个方向改变呢?
-
就像我们下山一样,如果遇到了雾,无法看见山路的全部走向,只能看见周围的一小片区域。那么就只能基于能看见的部分做一个决策。(忽略主观因素)如果想尽快下山的话,那么我们应该找最陡峭的方向,因为陡峭的路在海拔上变化更快。大方向确定了,那么现在可以在二维平面考虑这个问题。如果发现自己目前是在向上爬坡的,比如左图那样,说明我身后的海拔比我此时的海拔更低。因此,为了降低海拔,那么应当掉头向反方向走,这样更容易走到山脚,如图右边。
-
反之,如果此时发现自己是在向下走的,那么我应该继续前进,因为我前方的海拔比我此时的海拔低,我更容易走到山脚。在这个场景下,“上”坡和“下”坡,如果换用数学语言来描述,其实就是在坐标系下,这个山的斜率(梯度)符号。上坡就是斜率大于0,下坡就是斜率小于0。那上坡时,我们要选择的是 减小的方向,下坡时选择的是 增大的方向。也就是说我们总是沿着斜率的反方向来走的。
反向传播与更新参数——沿着模型相反的方向,从后向前地逐层计算每个神经元的损失,并更新参数。

- 在数学问题上,如果不知道一个函数的解析形式或者很难对函数进行微分计算的时候,就可以通过这样的思想,来搜索函数的最小值。 对于如下图所示的函数来说,要搜索最小值,当处于左侧点位时,斜率𝑘<0,应当朝正方向搜索,即𝛥𝑥>0, 如果位于右侧点位,𝑘>0,那么朝着副方向 的方向搜索。 回到三维甚至多维问题上进行讨论。在数学上,在某一点上,函数值变化最快,也就是所谓的最陡峭的方向,就是这一点梯度所在的方向。刚才已经得到了结论,如果要找最小值,应当朝梯度的反方向走。
- 这就是在更新时候使用的梯度下降算法,每次更新都是向着当前梯度的反方向更新一步。但应当注意到,梯度可以很大,如果完全按照梯度作为步长进行移动,有可能会错过一些最小值,因此通常会用一个系数,用来调整步长。这就是学习率learning rate,它是模型训练时一个重要的超参数。

- 那么,针对损失函数的权值的梯度如上所示。
- 这里𝛻𝐿就是损失函数的梯度,它本身也是个向量,它的多个维度分别由损失函数 对多个权值𝑊_𝑚𝑛求偏导所得。当梯度被解释为权值空间中的一个向量时,它就确定了陡峭上升的方向,那么梯度递减的训练法则就是:𝑤_𝑚𝑛 (𝑡+1)←𝑤_𝑚𝑛 (𝑡)+𝛥𝑤_𝑚𝑛,其中𝛥𝑤_𝑚𝑛=?𝜂 𝜕𝐿/(𝜕𝑤_𝑚𝑛 ), 为学习率,负号表示梯度的相反方向,因此梯度训练法则为: 𝑤_𝑚𝑛 (𝑡+1)←𝑤_𝑚𝑛 (𝑡)?𝜂 𝜕𝐿/(𝜕𝑤_𝑚𝑛 )

- 求解损失函数对各参数的偏导数就需要用到数学上的链式法则𝑑𝑢/𝑑𝑥=𝑑𝑢/𝑑𝑦?𝑑𝑦/𝑑𝑥,链式法则在偏微分中同样适用。如图所示为链式法则求各偏导示意图。其中:𝑧_0=𝑤_0 𝑥;𝑦_1=𝑓_1 (𝑧_0 );𝑧_1=𝑤_1 𝑦_1;𝑦_2=𝑓_2 (𝑧_1 );𝑧_2=𝑤_2 𝑦_2;𝑦_3=𝑓_3 (𝑧_2 )
- 那么如果要求最终的输出 对最初的权重 的偏导,应用链式法则,会得到: (𝜕𝑦_3)/(𝜕𝑤_0 )=(𝜕𝑦_3)/(𝜕𝑧_2 )×(𝜕𝑧_2)/(𝜕𝑦_2 )×(𝜕𝑦_2)/(𝜕𝑧_1 )×(𝜕𝑧_1)/(𝜕𝑦_1 )×(𝜕𝑦_1)/(𝜕𝑧_0 )×(𝜕𝑧_0)/(𝜕𝑤_0 )=𝑓_3^′×𝑤_2×𝑓_2^′×𝑤_1×𝑓_1^′×𝑥
参数更新前权重矩阵和计算结果。

一次反向传播后权重矩阵和计算结果。

分类问题

- DNN训练以解决分类问题我们已经学习过了,接下来看一下分类问题。
- 在数据的角度上,二者的区别主要在真值形式,分类问题的真值通常是one-hot编码过的向量。只有代表正确分类的元素为1,其余都为0。例如3分类问题,一条数据属于第二类,则它的真值应该是010。分类问题与回归问题的训练过程是一致的。主要区别的点在于输出层函数的选取和损失函数的选取。先看一下激活函数,分类问题一般使用softmax作为激活函数
- 在分类问题中,𝑘代表第𝑘类,𝑛是总分类数。𝑧_𝑘就是第𝑘个输出单元的输入值。因为分母是各类别输入之和,所以通过softmax函数,我们可以将数值转化成数据属于各分类的概率。各输出加和就应该为1。比如输入0.2,0.5经过了一个神经网络,在输出层经过softmax,得到二分类的概率是0.48和0.52 对于分类问题,常用的损失函数为交叉熵损失,将输出的二分类概率0.48和0.52带入得: "Loos "=0.73
4.1.2 代码实现
In [34]
import numpy
def sigmoid (x): #激活函数
return 1/(1+numpy.exp(-x))
def der_sigmoid(x): #激活函数的导数
return sigmoid(x)*(1-sigmoid(x))
def mse_loss(y_tr,y_pre): #均方误差损失函数
return((y_tr - y_pre)**2).mean()
class nerualnetwo():
def __init__(self): #感知神经元的权值属性定义,初始化随机值,会导致模型以及预测结果每次都不同
self.w1 = numpy.random.normal()
self.w2 = numpy.random.normal()
self.w3 = numpy.random.normal()
self.w4 = numpy.random.normal()
self.w5 = numpy.random.normal()
self.w6 = numpy.random.normal()
self.b1 = numpy.random.normal()
self.b2 = numpy.random.normal()
self.b3 = numpy.random.normal()
def feedforward(self,x): #前向计算方法,#返回所有神经元值
h1 = x[0]*self.w1+x[1]*self.w2+self.b1
h1f = sigmoid(h1)
h2 = x[0]*self.w3+x[1]*self.w4+self.b2
h2f = sigmoid(h2)
o1 = h1f*self.w5+h2f*self.w6+self.b3
of = sigmoid(o1)
return h1,h1f,h2,h2f,o1,of
def simulate (self,x): #前向计算方法,返回预测值
h1 = x[0]*self.w1+x[1]*self.w2+self.b1
h1f = sigmoid(h1)
h2 = x[0]*self.w3+x[1]*self.w4+self.b2
h2f = sigmoid(h2)
o1 = h1f*self.w5+h2f*self.w6+self.b3
of = sigmoid(o1)
return of
def train(self,data,all_y_tr):
epochs = 1000 #迭代次数
learn_rate = 0.1 #学习率
#print(self.w1)
for i in range(epochs):
for x , y_tr in zip(data,all_y_tr):
valcell = self.feedforward(x) #使用当前权值前向计算所有神经元值
#h1-cell[0],h1f-cell[1],h2-cell[2],h2f-cell[3],o1-cell[4],of-cell[5]
y_pre = valcell[5] #当前预测结果
#反向传播求导计算,每个节点或权值仅仅需要求导一次,即可覆盖下方所有节点
der_L_y_pre = -2*(y_tr-y_pre) #损失函数L对y_pre求导
#y_pre对h1f求偏导,y_pre就是of, of=sg(o1),o1= h1f*self.w5+h2f*self.w6+self.b3(w5后面做常数处理)
#用下一层的输出对上一层的输出逐层求偏导, 目的是求出对权值的偏导
#(权值是刻画数据的元数据,机器学习的目的就是以数据为依据求出刻画自身的元数据)
der_y_pre_h1f = der_sigmoid(valcell[4])*self.w5
der_y_pre_h2f = der_sigmoid(valcell[4])*self.w6
#print(valcell,der_y_pre_h2f)
#h1f对w1,w2求偏导
der_h1f_w1 = der_sigmoid(valcell[0])*x[0]
der_h1f_w2 = der_sigmoid(valcell[0])*x[1]
#h2f对w3,w4求偏导
der_h2f_w3 = der_sigmoid(valcell[2])*x[0]
der_h2f_w4 = der_sigmoid(valcell[2])*x[1]
#y_pre对w5w6b3求偏导
der_y_pre_w5 = der_sigmoid(valcell[4])*valcell[1]
der_y_pre_w6 = der_sigmoid(valcell[4])*valcell[3]
der_y_pre_b3 = der_sigmoid(valcell[4])
#h1f对b1求偏导
der_h1f_b1 = der_sigmoid(valcell[0])
#h2f对b2求偏导
der_h2f_b2 = der_sigmoid(valcell[2])
#反向传播,以损失函数为起点反向传播(通过求导链式法则)到各个权值参数
#梯度下降,调整权值,按照学习速率逐渐下降,学习率与梯度的乘积为下降步长。
#即权重和偏置每向前一步,就需要走学习率和当前梯度的乘积这么远
self.w1 -= learn_rate * der_L_y_pre * der_y_pre_h1f * der_h1f_w1
self.w2 -= learn_rate * der_L_y_pre * der_y_pre_h1f * der_h1f_w2
self.w3 -= learn_rate * der_L_y_pre * der_y_pre_h2f * der_h2f_w3
self.w4 -= learn_rate * der_L_y_pre * der_y_pre_h2f * der_h2f_w4
self.w5 -= learn_rate * der_L_y_pre * der_y_pre_w5
self.w6 -= learn_rate * der_L_y_pre * der_y_pre_w6
self.b1 -= learn_rate * der_L_y_pre * der_y_pre_h1f * der_h1f_b1
self.b2 -= learn_rate * der_L_y_pre * der_y_pre_h2f * der_h2f_b2
self.b3 -= learn_rate * der_L_y_pre *der_y_pre_b3
if i % 10 ==0 :
#对训练数据数组作为simulate函数的参数依次进行处理得到当前预测值
y_pred = numpy.apply_along_axis(self.simulate,1,data)
#对真实值与预测值两个数组使用损失函数求均方误差作为参数的评价标准
loss = mse_loss (all_y_tr , y_pred)
print(i,loss)
4.3 梯度消失和梯度爆炸
- 在机器学习的过程中,我们有时候会发现,随着训练轮数的增加,在验证结果并不很好的情况下,网络权重几乎不变了,这其实是很常见的一种问题,造成这种问题的原因有很多,其中一条是传播过程中的梯度消失,与之相对的也有可能出现参数有巨大变化的现象,它的原因可能是在传播过程中出现了梯度爆炸。
梯度消失——反向传播的过程,会有若干个小数,且是小于0.25的数相乘的情况。

- 对于sigmoid激活函数而言,它的函数曲线和导数曲线如图所示。可以看到当𝑥<?5或𝑥>5的时候,函数接近一条横线,此时斜率约等于0,即使是靠近0附近的线性区,斜率(梯度)也仅有0.25。
- Tanh是另一种常见的激活函数,它虽然0处的导数值为1,但是导数沿正负 轴的方向,下降的都非常快。且tanh依然有饱和区即导数约等于0的区域存在,其函数及其导数图像如右图所示。
- 如果一个深度网络模型使用了这两种激活函数,反向传播的过程,会有若干个小数,且是小于0.25的数相乘的情况,那么在靠近输入层的区域,梯度就会很小,权重的更新值就将接近于0。这就是我们所说的梯度消失。

- 还是以刚才讲解链式法则的例子说明(如图所示),我们刚才推导出了𝑦_3对𝑤_0的偏导数表达形式,我们以𝑓_1,𝑓_2,𝑓_3都是sigmoid函数进行计算。可以算出:
𝑧_0=𝑤_0 𝑥=0.06;𝑦_1=𝑓_1 (𝑧_0 )=0.515;𝑧_1=𝑤_1 𝑦_1=0.103𝑦_2=𝑓_2 (𝑧_1 )=0.525;𝑧_2=𝑤_2 𝑦_2=0.315;𝑦_3=𝑓_3 (𝑧_2 )=0.578
(𝜕𝑦_3)/(𝜕𝑤_0 )=(𝜕𝑦_3)/(𝜕𝑧_2 )×(𝜕𝑧_2)/(𝜕𝑦_2 )×(𝜕𝑦_2)/(𝜕𝑧_1 )×(𝜕𝑧_1)/(𝜕𝑦_1 )×(𝜕𝑦_1)/(𝜕𝑧_0 )×(𝜕𝑧_0)/(𝜕𝑤_0 )=𝑓_3^′×𝑤_2×𝑓_2^′×𝑤_1×𝑓_1^′×𝑥 =0.000036
- 可以看到,偏导数的值小于 ,是一个非常小的量了。
Relu函数
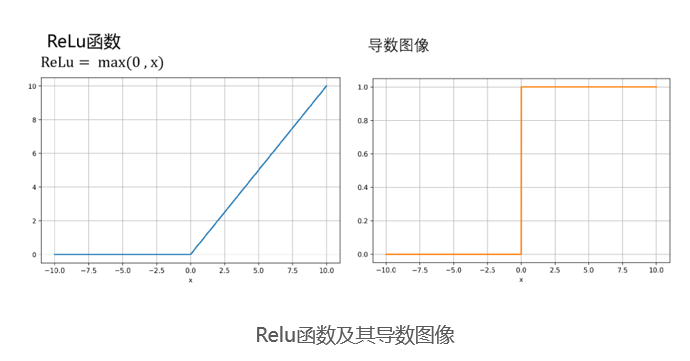
- 为了缓解梯度消失问题,我们可以使用ReLU函数,作为激活函数。如下图所示,只要𝑥大于0,导数就是。那么反向传播过程中偏导数相乘结果的绝对值就不会越来越小了。梯度下降问题可以得到缓解。
梯度爆炸 — 当初始的权重过大(如大于10)时,在反向传播的过程中会造成梯度呈指数增长,在靠近输入层的位置,由于梯度过大,导致权重有非常大的更新。

- 刚刚讲完了梯度下降现象,接下来介绍梯度爆炸现象,梯度爆炸的主要原因不在激活函数,而在于模型的权重,梯度爆炸: 当初始的权重过大(如大于10)时,在反向传播的过程中会造成梯度呈指数增长,在靠近输入层的位置,由于梯度过大,导致权重有非常大的更新。
- 如果一个模型,激活函数都选用了ReLU,而权重的绝对值都很大,那么反向传播过程会发生些什么呢?感兴趣的同学可以自己试一下。
- 想要缓解梯度爆炸,一个常见的做法是优化初始化权重,如使用正态分布的初始化权重。更多的方法就不展开介绍了。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【C语言】预处理详解
- 记一次NAS问题修复,挂载的硬盘名称发生变化导致文件上传失败,解决问题方案总结
- Visual Studio 2013 中创建一个基于 Qt 的动态链接库:并在MFC DLL程序中使用
- typora的使用保姆级教程以及安装后的配置方式
- Rust 中的 Option、Result 和 ? 运算符
- 使用JavaScript实现一个复杂功能:日期范围选择器
- Python小工具——开发一个加密解密的小应用 & windows下可执行文件exe制作
- K8S网络类型
- 数学对象使用方法 -- JavaScript
- 【Java】多线程与JUC