priority_queue的使用与模拟实现（容器适配器+stack与queue的模拟实现源码）

引言（容器适配器）

在STL中，有这样一种“容器”，自身并不完成对数据的操作，而是以其底部的容器来完成所有对数据的工作，类似于对容器的封装。这种“容器”称为container adapter（容器适配器）

stack（栈），queue（队列），priority_queue（优先级队列）都是容器适配器。
栈与队列的实现大家可以参考之前C语言的栈和队列实现，关于stack与queue容器适配器的实现会放在文末：
戳我看栈的模拟实现哦
戳我看队列的模拟实现哦

这篇文章就来介绍一下优先级队列的使用与实现：
（优先级队列的实现需要具备堆数据结构的知识，可以查看相关文章戳我看堆详解哦，戳我看堆排序详解哦）

priority_queue的介绍与使用

priority_queue介绍

优先级队列与队列类似，我们不能随意访问其中的元素，只能访问队头的首元素。但是在优先级队列中，根据某种优先级（某个标准），任意时刻队列的首元素都会是整个队列中优先级最高的元素（默认情况下队头的元素为最大的元素，可以通过迪三个模板参数来调整）；

优先级队列的底层容器必须实现有empty()、 size()、 front()、 push_back()、 pop_back()。默认的底层容器为vector；

优先级队列的结构类似于堆结构，堆结构可以使堆顶的元素为所有元素中最大/小的元素（通过建大堆或小堆来实现）。所以优先级队列的底层实现其实就是堆结构。在容器适配器中会在需要的时刻建堆，以保证优先级队列队头的元素始终是整个队列中优先级最高的。

优先级队列有三个模板参数：
第一个参数 T即优先级队列中存储的数据类型（默认为vector）；
第二个参数 Container即优先级队列使用的底层容器类型；
第三个参数 Compare是一个仿函数类型，即优先级的比较接口类型（默认为less<T>，即当第一个参数的优先级小于第二个元素时返回真，与之相反的仿函数为greater。less/greater都是库实现的，底层调用T类型的<与>）。

接口使用

默认成员函数

构造

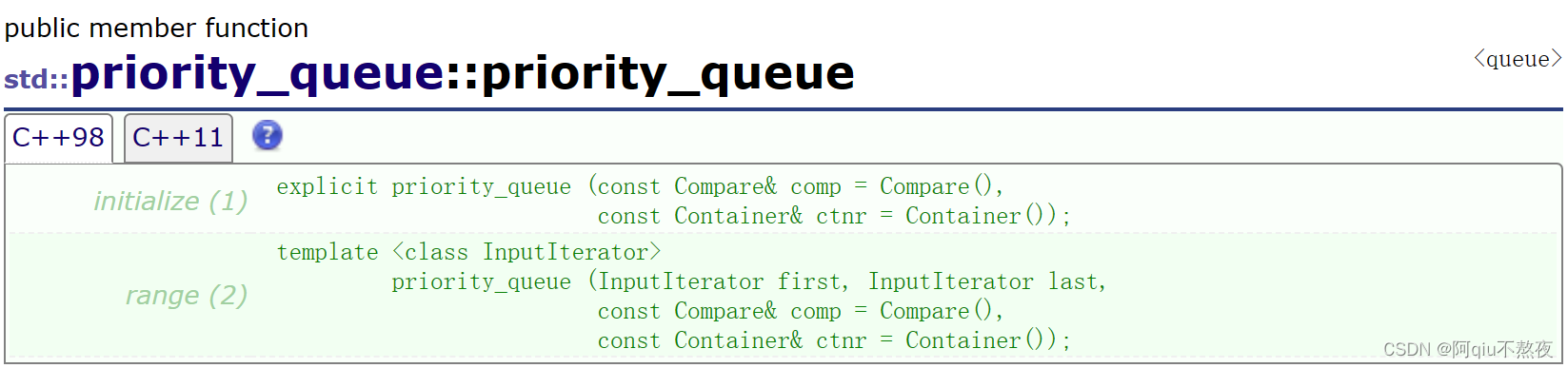
优先级队列的构造函数有两种重载版本，即无参构造与使用迭代器区间构造（在构造函数中会使用指定底层容器与比较仿函数的默认构造函数来初始化一个容器对象仿函数对象，所以我们传参构造的时候可以不用去管它们）；
对于迭代器区间构造，这是一个函数模板，即可以通过任意一种InputIterator迭代器来构造优先级队列：

int main()
{
	vector<int> v(10);
	for (int i = 0; i < 10; ++i)
	{
		v[i] = i + 1;
	}

	priority_queue<int> pq1; //无参构造
	priority_queue<int> pq2(v.begin(), v.end()); //迭代器区间构造
	cout << pq2.top() << endl;

	priority_queue<int, vector<int>, greater<int>> pq3(v.begin(), v.end()); //指定优先级
	cout << pq3.top() << endl;

	return 0;
}

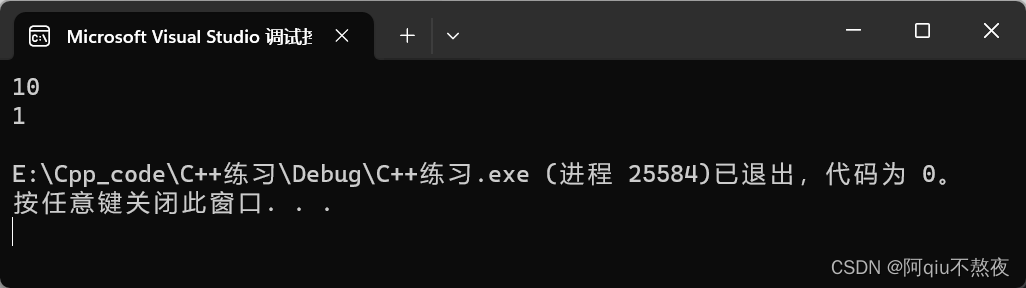
pq1使用无参构造；
pq2使用迭代器v的begin与end构造，默认的优先级队列头为最大值；
pq3使用v迭代器区间构造的同时，指定了优先级比较的仿函数，队列头为最小值。

优先级队列的包装器没有定义拷贝构造，赋值运算符重载、析构函数，因为编译器会自动生成，自动生成的这些默认成员函数会去调用底层容器的这些默认成员函数。

size与empty

size用于获取优先级队列中元素的个数；

empty用于返回优先级队列是否为空：为空返回真，否则返回假：

int main()
{
	vector<int> v(10);
	for (int i = 0; i < 10; ++i)
	{
		v[i] = i + 1;
	}

	priority_queue<int> pq(v.begin(), v.end()); //迭代器区间构造
	cout << pq.size() << endl;
	cout << pq.empty() << endl;

	return 0;
}

top

top用于获取优先级队列头的元素：

int main()
{
	vector<int> v(10);
	for (int i = 0; i < 10; ++i)
	{
		v[i] = i + 1;
	}

	priority_queue<int> pq(v.begin(), v.end()); //迭代器区间构造
	cout << pq.top() << endl;

	return 0;
}

push与pop

push用于在优先级队列中插入一个元素，由于优先级队列会维持队列头的元素始终优先级最大，所以我们不能进行随机插入：

int main()
{
	vector<int> v(10);
	for (int i = 0; i < 10; ++i)
	{
		v[i] = i + 1;
	}

	priority_queue<int> pq(v.begin(), v.end()); //迭代器区间构造
	cout << "before top:" << pq.top() << endl;

	pq.push(12);
	cout << "after top:" << pq.top() << endl;

	return 0;
}

pop用于在优先级队列中删除队列头的元素，即删除优先级最高的那个元素：

int main()
{
	vector<int> v(10);
	for (int i = 0; i < 10; ++i)
	{
		v[i] = i + 1;
	}

	priority_queue<int> pq(v.begin(), v.end()); //迭代器区间构造
	cout << "before top:" << pq.top() << endl;

	pq.pop();
	cout << "after top:" << pq.top() << endl;

	return 0;
}

priority_queue的模拟实现

为避免命名冲突，我们创建一个新的命名空间qqq来放我们的模拟实现；
作为一个类模板，有三个模板参数；
在优先级队列中需要两个成员变量：底层的容器对象与仿函数对象：

namespace qqq 
{
    template <class T, class Container = vector<T>, class Compare = less<T> >
    class priority_queue
    {
    
    private:
        Container c;
        Compare comp;
    };
};

需要提醒的是：这里的Container与Compare是底层容器与仿函数的类型，用这两个类型创建的c与comp才是容器对象与仿函数对象，在传参或者指定模板参数时不要搞错了。

构造函数

除了构造函数之外的其余默认成员函数，系统生成的默认成员函数会调用底层容器的默认成员函数，就足够了。

对于无参构造，我们其实不需要去实现，但是因为要实现迭代器区间构造，所以编译器不会再生成一个默认构造函数，所以我们写一个接口即可：

    priority_queue()
    {}

对于迭代器区间构造，这是一个函数模板：
我们首先通过循环遍历将迭代器区间中的元素拷贝到优先级队列中的成员容器c中；
然后通过循环调用向下调整建堆的成员函数adjust_down实现队列顶的元素优先级最高（对于已有的数组，向下调整建堆的效率要略高于向上调整建堆，这一点在后面详细介绍这两个建堆函数时会介绍）：

    template <class InputIterator>
    priority_queue(InputIterator first, InputIterator last) //向下调整建堆
    {
        while (first != last) //遍历拷贝
        {
            c.push_back(*first);
            ++first;
        }
        for (int i = (c.size() - 2) / 2; i >= 0; --i) //向下调整建堆
        {
            adjust_down(i);
        }
    }

size与empty

size与empty的实现就是调用底层容器的size与empty接口即可，这也是为什么要求底层容器必须要定义有这些接口：

    bool empty() const
    {
        return c.empty();
    }
    size_t size() const
    {
        return c.size();
    }

top

top函数在库实现中，调用了底层容器的front接口，返回值为T&；
我们在模拟实现时直接返回c的第一个元素即可：

    T& top() const
    {
        return c[0];
    }

push与pop

对于 push 函数：
首先调用底层容器的push_pack在底层容器尾插入一个元素；
然后使用向上调整建堆将新插入的元素调整至正确的位置，保证队列头的元素为优先级最大的元素：

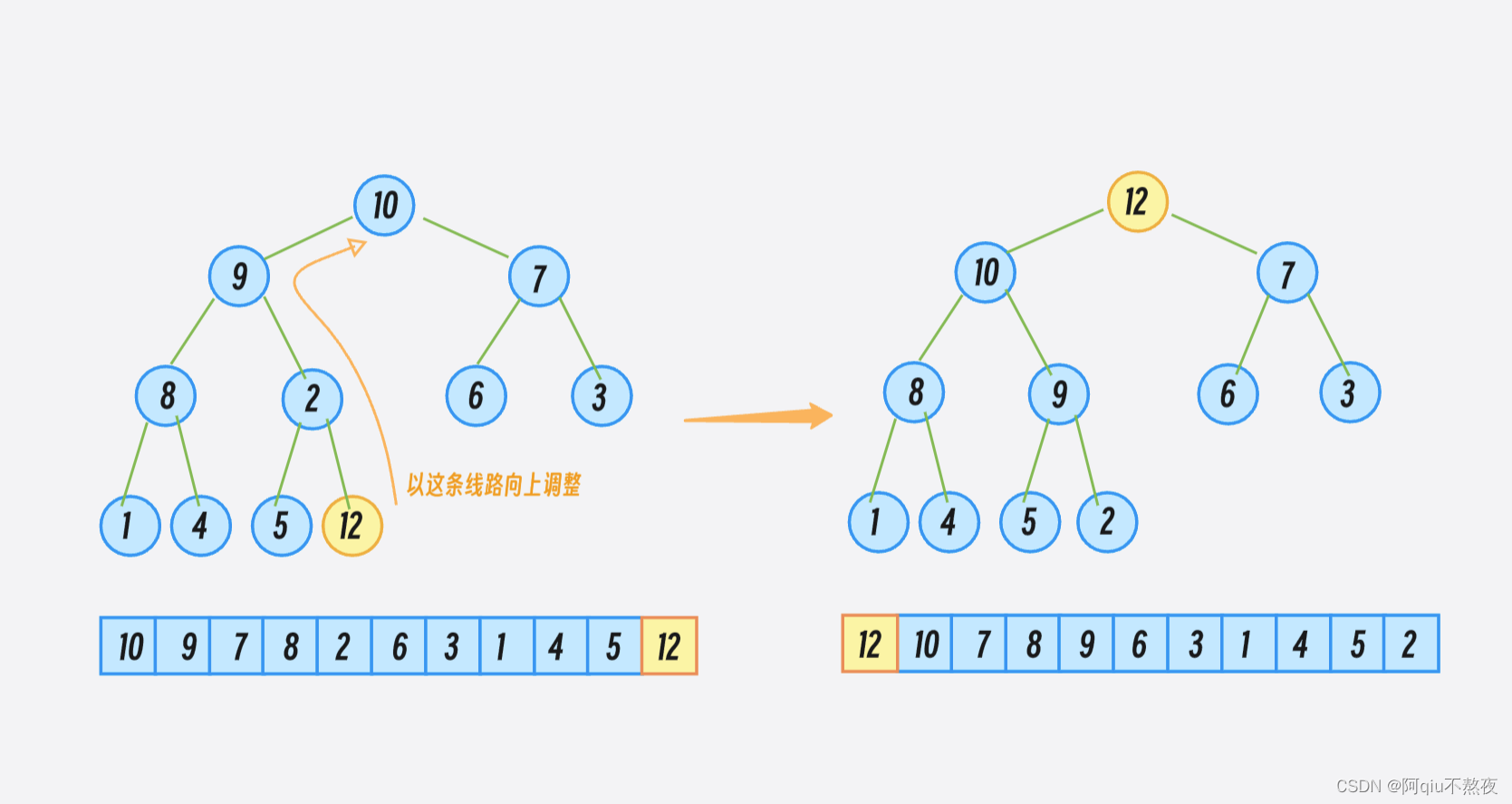
    void push(const T& x)
    {
        c.push_back(x);
        adjust_up(c.size() - 1);
    }

对于 pop 函数：
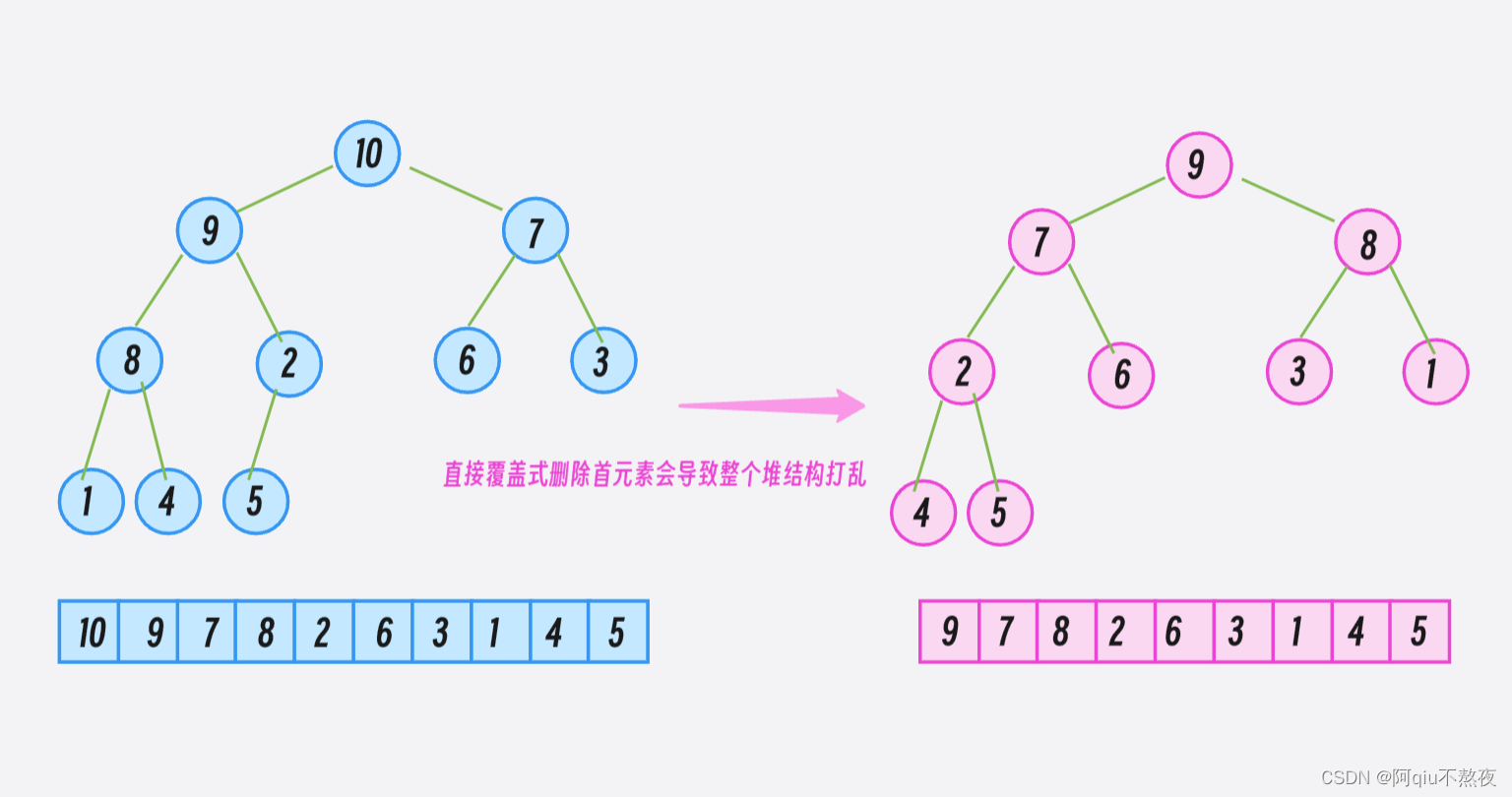
因为如果直接将底层容器中的元素整体向前移动一个元素来删除第一个元素的话，就会破坏整个堆结构。所以在这里先将底层容器中的首尾元素互换，这样只破坏了一个元素的堆的位置，并且使要删除的元素正好处于底层容器的尾部。
在pop_pack删除尾元素后，再将那个被交换到堆顶的元素通过向下调整建堆移动到正确的位置即可：

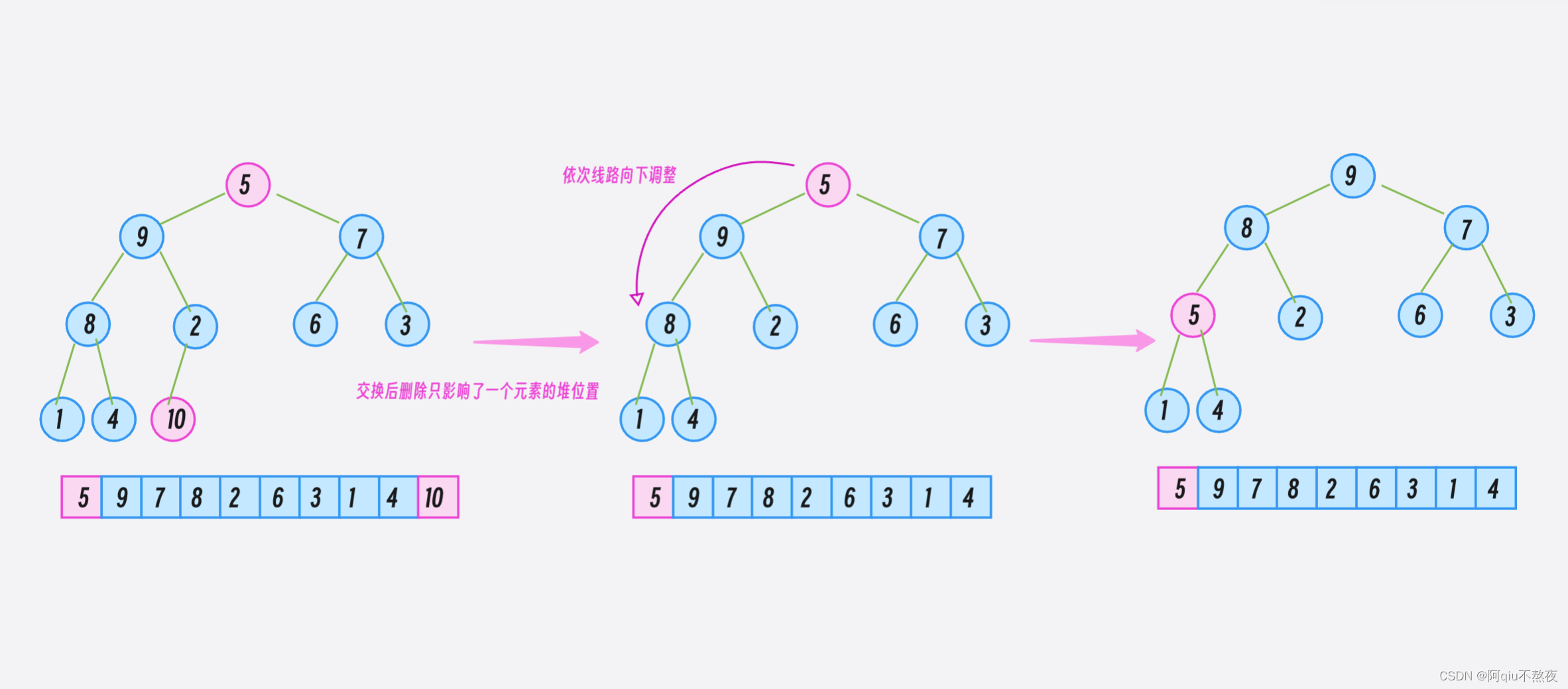
    void pop() //Remove top element
    {
        //交换后pop，再向下调整
        swap(c[0], c[c.size() - 1]);
        c.pop_back();
        adjust_down(0);
    }

向上调整建堆与向下调整建堆

关于堆这个数据结构的详细知识，可以参考我之前的文章：戳我看堆详解哦

这里只提一个要点，即结点数据的下标与结点位置的规律：
父亲结点的下标 = (孩子结点下标-1)/2；
左孩子结点的下标 = 父亲结点的下标2+1；
右孩子结点的下标 = 父亲结点的下标2+2。
这些规律使我们在根据逻辑结构访问堆中的元素时，会很方便。

向上调整建堆

向上调整建堆就是将元素由下到上调整至合适的位置：
类似于二叉树的尾插，然后将尾插的元素向上调整放到合适的位置（若子节点的值小于父亲结点的值，就将父子结点的值交换，直到再次形成一个大堆）：

   void adjust_up(int child)
    {
        assert(0 <= child && child < size());
        while (child > 0)
        {
            int parent = (child - 1) / 2;

            if (comp(c[parent], c[child]))
            {
                swap(c[parent], c[child]);
            }

            child = parent;
        }
    }

向下调整建堆

向下调整建堆就是将元素由上到下调整至合适的位置：
向下调整建堆时，即将每一个根结点向下调整，放在其合适的位置。这要求该根的子树都是正确的大堆，所以我们需要从倒数第二层的根结点开始向下调整（比较父亲结点与较大的子结点的值，若父亲结点小于较大的子节点，则交换它们的值。直到再次形成大堆）：

    void adjust_down(int parent)
    {
        assert(0 <= parent && parent < size());
        int bigger_child = parent * 2 + 1;
        while (bigger_child < size())
        {
            if (bigger_child + 1 < size() && comp(c[bigger_child], c[bigger_child + 1]))
            {
                ++bigger_child;
            }
            
            if (comp(c[parent], c[bigger_child]))
            {
                swap(c[parent], c[bigger_child]);
            }

            parent = bigger_child;
            bigger_child = parent * 2 + 1;
        }
    }

（这里示意图就不画了，在关于堆的详解中有详细的图示）

关于在对整个数组的数据进行建堆时，为何向下调整建堆的效率高于向上调整建堆的效率，这里做简单的说明（大家可以去计算他们的时间复杂度，这里只从逻辑上分析）：
面对一个未成形的堆，最后一行的元素个数是最多的，向上调整建堆从最后一层的最后一个元素向上调整，每个元素最大需要调整高度次。即最多的元素需要调整最多的次数；
而向下调整建堆从倒数第二行的最后一个元素开始向下调整，每个元素最大只需要调整一次。即最多的元素需要调整最少的次数。在向下调整建堆中，最多需要调整高度次的元素只有一个，那就是堆顶的元素。
所以向下调整建堆相对于向上调整建堆的效率较高，但他们都属于n*logn级的时间复杂度，效率都很高。

源码概览

priority_queue模拟实现源码：

namespace qqq 
{
    template <class T, class Container = vector<T>, class Compare = less<T> >
    class priority_queue
    {
    private:
        void adjust_up(int child)
        {
            assert(0 <= child && child < size());

            while (child > 0)
            {
                int parent = (child - 1) / 2;

                if (comp(c[parent], c[child]))
                {
                    swap(c[parent], c[child]);
                }

                child = parent;
            }
        }
        void adjust_down(int parent)
        {
            assert(0 <= parent && parent < size());

            int bigger_child = parent * 2 + 1;
            while (bigger_child < size())
            {
                if (bigger_child + 1 < size() && comp(c[bigger_child], c[bigger_child + 1]))
                {
                    ++bigger_child;
                }

                if (comp(c[parent], c[bigger_child]))
                {
                    swap(c[parent], c[bigger_child]);
                }

                parent = bigger_child;
                bigger_child = parent * 2 + 1;
            }
        }
    public:
        priority_queue()
        {}

        template <class InputIterator>
        priority_queue(InputIterator first, InputIterator last) //向下调整建堆
        {
            while (first != last)
            {
                c.push_back(*first);
                ++first;
            }
            for (int i = (c.size() - 2) / 2; i >= 0; --i)
            {
                adjust_down(i);
            }
        }
        bool empty() const
        {
            return c.empty();
        }
        size_t size() const
        {
            return c.size();
        }
        T& top() const
        {
            return c[0];
        }
        void push(const T& x)
        {
            c.push_back(x);
            adjust_up(c.size() - 1);
        }
        void pop() //Remove top element
        {
            //交换后pop，再向下调整
            swap(c[0], c[c.size() - 1]);
            c.pop_back();
            adjust_down(0);
        }

		//测试代码
        //void print()
        //{
        //    for (auto e : c)
        //    {
        //        cout << e << " ";
        //    }
        //}
    private:
        Container c;
        Compare comp;
    };

};

stack与queue模拟实现源码：

namespace qqq
{

    //stack
    template<class T, class Con = deque<T>>
    class stack
    {
    public:

        stack()
        {}

        void push(const T& x)
        {
            _c.push_back(x);
        }
        void pop()
        {
            if (_c.empty())
                return;
            _c.pop_back();
        }
        T& top()
        {
            return _c.back();
        }
        const T& top()const
        {
            return _c.back();
        }
        size_t size()const
        {
            return _c.size();
        }
        bool empty()const
        {
            return _c.empty();
        }

    private:
        Con _c;
    };

    //queue
    template<class T, class Con = deque<T>>
    class queue
    {
    public:

        queue()
        {}

        void push(const T& x)
        {
            _c.push_back(x);
        }
        void pop()
        {
            if (_c.empty())
                return;
            _c.pop_front();
        }
        T& back()
        {
            return _c.back();
        }
        const T& back()const
        {
            return _c.back();
        }
        T& front()
        {
            return _c.front();
        }
        const T& front()const
        {
            return _c.front();
        }
        size_t size()const
        {
            return _c.size();
        }
        bool empty()const
        {
            return _c.empty();
        }
    private:
        Con _c;
    };
};

总结

到此，关于priority_queue的使用与实现的所有知识就介绍完了
由于堆的知识在之前C语言部分有详细介绍，所以在这篇文中介绍的不是特别详细，大家有需要可以跳转去相关文章，蟹蟹支持

如果大家认为我对某一部分没有介绍清楚或者某一部分出了问题，欢迎大家在评论区提出

如果本文对你有帮助，希望一键三连哦

希望与大家共同进步哦