NOIP2003提高组T4:传染病控制
题目链接
题目描述
近来,一种新的传染病肆虐全球。蓬莱国也发现了零星感染者,为防止该病在蓬莱国大范围流行,该国政府决定不惜一切代价控制传染病的蔓延。不幸的是,由于人们尚未完全认识这种传染病,难以准确判别病毒携带者,更没有研制出疫苗以保护易感人群。于是,蓬莱国的疾病控制中心决定采取切断传播途径的方法控制疾病传播。经过 WHO(世界卫生组织)以及全球各国科研部门的努力,这种新兴传染病的传播途径和控制方法已经研究清楚,剩下的任务就是由你协助蓬莱国疾控中心制定一个有效的控制办法。
研究表明,这种传染病的传播具有两种很特殊的性质;
- 第一是它的传播途径是树型的,一个人 X X X 只可能被某个特定的人 Y Y Y 感染,只要 Y Y Y 不得病,或者是 X Y XY XY 之间的传播途径被切断,则 X X X 就不会得病。
- 第二是,这种疾病的传播有周期性,在一个疾病传播周期之内,传染病将只会感染一代患者,而不会再传播给下一代。
这些性质大大减轻了蓬莱国疾病防控的压力,并且他们已经得到了国内部分易感人群的潜在传播途径图(一棵树)。但是,麻烦还没有结束。由于蓬莱国疾控中心人手不够,同时也缺乏强大的技术,以致他们在一个疾病传播周期内,只能设法切断一条传播途径,而没有被控制的传播途径就会引起更多的易感人群被感染(也就是与当前已经被感染的人有传播途径相连,且连接途径没有被切断的人群)。当不可能有健康人被感染时,疾病就中止传播。所以,蓬莱国疾控中心要制定出一个切断传播途径的顺序,以使尽量少的人被感染。
你的程序要针对给定的树,找出合适的切断顺序。
输入格式
输入格式:
第一行是两个整数
n
n
n 和
p
p
p。
接下来
p
p
p 行,每一行有
2
2
2 个整数
i
i
i 和
j
j
j,表示节点
i
i
i 和
j
j
j 间有边相连。(意即,第
i
i
i 人和第
j
j
j 人之间有传播途径相连)。其中节点
1
1
1 是已经被感染的患者。
输出格式
1 1 1 行,总共被感染的人数。
样例 #1
样例输入 #1
7 6
1 2
1 3
2 4
2 5
3 6
3 7
样例输出 #1
3
提示
对于 100 % 100\% 100% 的数据, 1 ≤ n ≤ 300 1 \leq n \leq 300 1≤n≤300。
算法思想
根据题目描述,可以分析出下面一些有用的信息:
- 传染病的传播途径是树型的
- 在一个疾病传播周期内,只能设法切断一条传播途径
- 根节点 1 1 1 是已经被感染的患者
也就是求针对给定的树,每层“切断”一条边后,最少剩余多少个节点?求剩余节点的最小值,考虑是否能用贪心解决?
贪心(一)
- 自底向上,每次切断剩余子节点多的子树,如下图左侧红色标记处。
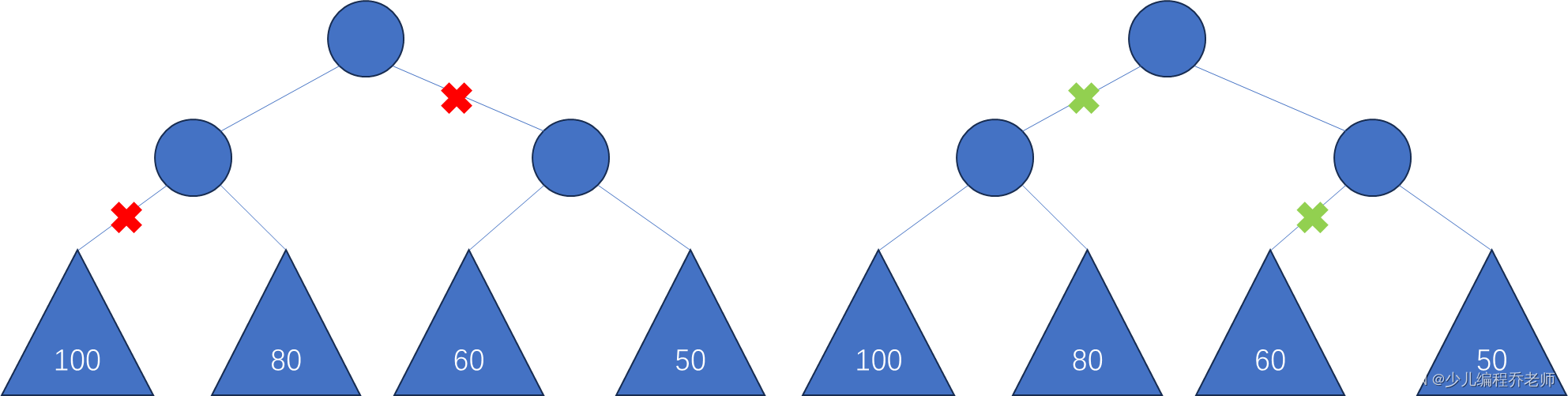
显然这种贪心策略不可取。如果自底向上按红色标记删除,剩余节点数为 82 82 82个;而按右侧绿色标记删除,剩余节点数为 52 52 52。
贪心(二)
- 自顶向下,每次切断子节点多的子树,如下图左侧红色标记处。
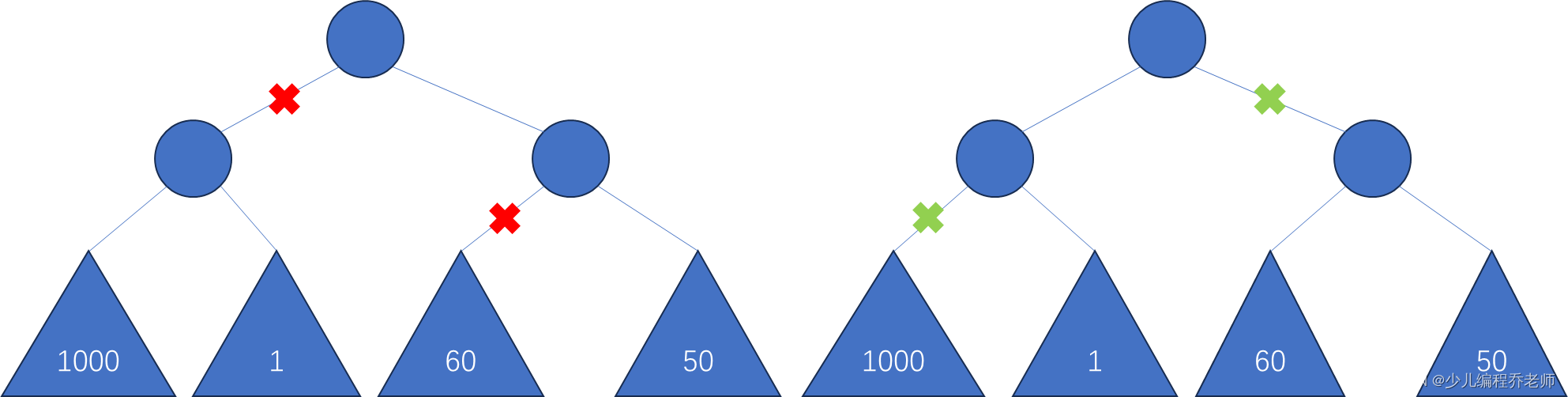
这种贪心策略也不可取。如果自顶向下按红色标记删除,剩余节点数为 52 52 52个;而按右侧绿色标记删除,剩余节点数为 3 3 3。
由此可见,以上两种贪心策略皆不可取。
暴力枚举
由于题目中的数据范围较小, 1 ≤ n ≤ 300 1 \leq n \leq 300 1≤n≤300,因此可以尝试枚举每层要切断的边,直接暴力搜索出所有方案,求其中最小值即可。
为了提高搜索效率,可以预处理出下面的信息:
- 每一层所有边的集合,第 i i i层的所有边用 d ( i ) \text{d}(i) d(i)表示
- 每棵子树的节点个数,以 u u u为根的子树包含 si ( u ) \text{si}(u) si(u)个节点
然后从根节点开始,枚举每一层要切断的边,也就是要删除的子树:
- 将子树的所有边标记成切断状态
- 从总节点数中减去该子树中的节点数
- 递归处理树的下一层
- 回溯时,要恢复被切断子树的状态
时间复杂度
暴力枚举的时间复杂度与树的深度和每层的节点数有关。在最坏情况下的时间复杂度是 O ( 2 n ) O(2^n) O(2n)。
在自顶向下搜索过程中,会对已经切断的子树中的所有边进行标记,因此在递归搜索时,不会处理已经标记的边。这样剪枝在很大程度上提升了搜索效率,外加数据也比较水,是可以通过的。
代码实现
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
const int N = 305, M = N * 2; //无向边*2
int h[N], e[M], ne[M], idx; //链式前向星
int n, p, ans = N;
vector<int> d[N]; //d[i]表示第i层边的集合
int si[N]; //si[u]表示以u为根的子树的节点个数
int st[M]; //用来标记边是否被切断
void add(int a, int b) // 添加一条边a->b
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
//预处理每层边的集合和子树的节点个数
int work(int u, int depth, int fa)
{
si[u] = 1; //子树的节点个数
for(int i = h[u]; ~ i; i = ne[i]) //遍历邻边
{
int v = e[i]; //子节点
if(v == fa) continue;
si[u] += work(v, depth + 1, u); //累加子树的节点
d[depth].push_back(i); //将边添加到depth层的集合中
}
return si[u];
}
//标记边j所指向的子树
void fill(int j, int color)
{
st[j] = color;
for(int i = h[e[j]]; ~ i; i = ne[i])
{
if(i != (j ^ 1))//i不是j的反向边,注意加括号
fill(i, color);
}
}
//暴力搜索所有切断方案,保留最小值
void dfs(int depth, int sum)
{
ans = min(ans, sum);
//枚举当前层所有边
for(int i = 0; i < d[depth].size(); i ++)
{
int j = d[depth][i]; //取出要切断的边
if(!st[j])
{
fill(j, 1); //将子树的所有边进行标记
dfs(depth + 1, sum - si[e[j]]);
fill(j, 0);//回溯恢复现场
}
}
}
int main()
{
cin >> n >> p;
memset(h, -1, sizeof h);
for(int i = 0; i < p ; i ++)
{
int a, b;
cin >> a >> b;
add(a, b), add(b, a); //双向建边
}
//预处理每层边的集合和子树的节点个数
work(1, 0, 0); //1为根节点,第0层,没有父节点
dfs(0, n); //从第0层开始,暴力搜索所有切断方案
cout << ans << endl;
return 0;
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Talk|斯坦福大学史浩辰:学习结构化世界模型用于现实世界中柔性物体的操控
- 最终Docker6:nacos集群部署
- 问题:github上不了,但是其他网页可以正常打开
- 【深度解析C++之运算符重载】
- kubernetes ResourceQuotas Limits(资源配额)
- BMI指数测试程序
- [Java]判断两个数据集是否相同
- 有道开源RAG引擎 QAnything 版本更新啦
- STM32Cubemx PWM驱动加湿器模拟火山喷发效果
- AI-ChatGPT&Copilot