Chip and Ribbon Educational Codeforces Round 158 (Rated for Div. 2)

Problem - B - Codeforces

题目大意：有一个n个数的数组a，有一个初始等于1的指针，有两种操作：

1.设指针当前位置为l，可以选择一个任意位置r(r>=l)，使[l,r]内所有数+1

2.将指针移动到一个任意位置，并令那个位置上的数+1

问对于一个初始有n个0的数组，最少要多少次操作2能使其等于a数组

1<=n<=2e5;0<=a[i]<=1e9;a[1]>=1

思路：因为要操作2次数最少，所以就要让操作1尽量发挥他的作用，那么就让每一次操作1从当前需要+1的位置开始，一直走到当前位置后面最右边的需要+1的位置，这样就可以把问题抽象成一个搭积木问题，像a=[1,2,4,5,3,4,2,1]时的积木如下图：

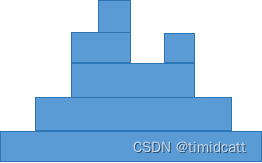
可以发现每一块积木刚好用一次操作1即可，操作2实际上就是从一个积木转移到另一个，那么操作2的次数其实就是积木数-1，积木数量增加的时候，也就是a[i]值增大的时候，增加的数目就是a[i]增加的值，所以最终操作2的数量也就是max(0,a[i]-a[i-1])

#include<bits/stdc++.h>
//#include<__msvc_all_public_headers.hpp>
using namespace std;
typedef long long ll;
const int N = 2e5 + 5;
const ll MOD = 1e9 + 7;
int n;
int m;
ll a[N];
void init()
{
    
}
void solve()
{
    cin >> n;
    a[0] = 1;//因为a[1]初始就是1，所以a[0]也要是1，防止差分为1
    init();
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
    }
    ll ans = 0;
    for (int i = 1;i <= n; i++)
    {
        if (a[i] > a[i - 1])
        {//加上所有大于0的差分
            ans += a[i] - a[i - 1];
        }
    }
    cout << ans;
    cout << '\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}