【算法提升—力扣每日一刷】五日总结【12/25--12/29】
LeetCode每五日一总结【12/25–12/29】
2023/12/25
双锁实现阻塞队列
双锁实现的阻塞队列主要用于解决多线程环境下的生产者-消费者问题。
在多线程环境中，当存在一个或多个生产者线程和一个或多个消费者线程同时访问共享队列时，可能会出现以下问题：
竞态条件（Race Condition）：由于多个线程同时对队列进行读写操作，可能导致数据不一致或错误结果。
队列溢出：如果生产者线程不受限制地往队列添加元素，而消费者线程无法及时消费，队列可能会溢出并导致内存泄漏等问题。
队列为空或满时的等待与唤醒：当消费者线程试图从空队列中获取元素时，或生产者线程试图向已满队列中添加元素时，需要进行等待，并在合适的时机被唤醒。
使用双锁机制实现的阻塞队列可以解决以上问题。通过互斥锁（例如 ReentrantLock）和条件变量（Condition），可以确保在队列为空时消费者线程等待，队列已满时生产者线程等待，并能够在合适的时机唤醒等待的线程，从而实现线程安全的生产者-消费者模型。这样可以避免竞态条件、队列溢出和等待与唤醒的问题，确保共享队列的正确操作。
2023/12/26
215.数组中的第K个最大元素（堆数据结构实现）
利用小顶堆的数据结构解答这道题目：
? 首先，我们先实例化一个小顶堆用来存放数组中的前K大元素，逻辑为：遍历数组，向小顶堆中放入K个数组中的元素，从第K+1个元素开始，分别与小顶堆中的堆顶元素做比较，如果数组中的元素大于小顶堆的堆顶元素，则替换小顶堆的堆顶元素，当数组遍历完成，返回小顶堆的堆顶元素即为数组中的第K大元素。
? 小顶堆数据结构是一个二叉堆数据结构，其中每个元素的子元素存储在一个较低级别的数组中。在最小堆中，父元素总是小于其子元素。
小顶堆总结-使用场景：
? 小顶堆是一种特殊的二叉堆数据结构，它具有以下特点：**父节点的值小于或等于其子节点的值。**小顶堆通常用来解决以下问题：
- 堆排序：小顶堆是实现堆排序算法的关键。借助小顶堆，可以对一个无序数组进行原地排序，时间复杂度为O(nlogn)。
- 求top K问题：通过维护一个大小为K的小顶堆，可以高效地找到一个数据集中最大（或最小）的K个元素。
- 优先级队列：小顶堆可以作为优先级队列的底层实现，用于按照一定的优先级顺序处理任务。每次取出最小元素，保证优先级最高的任务能够被提前处理。
- 贪心算法：在一些贪心算法中，需要不断选取当前最小的元素进行操作。小顶堆提供了高效的查找和删除最小元素的操作。
- 中位数问题：使用两个堆（一个小顶堆、一个大顶堆），可以快速获取数据流的中位数。
总之，小顶堆可以在许多数据处理和算法问题中提供高效的解决方案，特别是那些需要频繁查找和删除最小元素的情况。
2023/12/27
703.数据流中的第K大元素
方法一：利用自定义小顶堆对象
? 首先，先实例化一个容量为K的小顶堆，每次操作数据流中的数据前，先判断当前小顶堆是否已经满，如果小顶堆没有满，则直接将数据流中的数据offer到小顶堆中，如果小顶堆已经满了，则判断小顶堆中堆顶元素与数据流中元素的大小，如果数据流中元素大于堆顶元素，则将堆顶元素替换，最后返回的堆顶元素即为数据流中的第K大元素。
方法二：优先级队列
? 因为优先级队列底层的实现方式也是基于小顶堆，所以这两个方法在本质上没有很大的区别，但是由于优先级队列在jdk中有现成的对象，不需要我们自定义，因此简化了很多操作，只需要直接实例化一个优先级队列对象
PriorityQueue即可。
2023/12/28
295.数据流中的中位数
解答此题需要同时用到小顶堆和大顶堆两个数据结构，逻辑如下：
? 实例化一个大顶堆用来存放总数据中左侧数据部分，实例化一个小顶堆用来存放总数据中右侧数据部分，每次将数据流中的对象正确的加入到这两个堆中，具体加入方法如下：
? 因为要返回中位数，因此，当大顶堆与小顶堆中数据个数相同时，返回大顶堆堆顶元素与小顶堆堆顶元素的平均数即可，如果大顶堆与小顶堆中数据个数不相同时，返回大顶堆堆顶元素。（因为我们默认如果大顶堆与小顶堆数据个数相同时加入元素向大顶堆中添加，因此如果两堆数据个数不同，一定是大顶堆数据个数更多）
? 如何保证在加入数据时两堆中元素个数之差<1呢？
? 我们这里有一个很巧妙的算法，就是我们默认当两堆元素个数相同时，将大顶堆中的元素个数加一，但我们不能直接将数据加入到大顶堆中，我们采用先将数据加入到小顶堆中，再将小顶堆中的最小元素（poll）加入到大顶堆中去，这样可以保证我们两堆堆顶就是我们想要的中位数
? 上面说了如果两堆数据个数相同时元素入堆的策略，同样的，如果两堆元素个数不相同时，此时一定是小顶堆中的元素个数更少，我们采用先将元素加入到大顶堆中去，在将大顶堆中的最大元素（poll）加入到小顶堆中。
? 最后，当我们把数据流中的元素都通过上述规则加入到我们定义的两个堆中时，获取中位数的方法为：
? 判断两堆中的元素个数，if(两堆中元素个数相同) 返回两堆中堆顶元素的平均值即为中位数。
? if(两堆中元素个数不相同)返回大顶堆中的堆顶元素即为中位数。
2023/12/29
动态大/小顶堆
这个数据结构是一段代码整合了我们的大顶堆和小顶堆两种数据结构，同时我们加入了动态扩容的方式，使得在初始化堆数组时，不用考虑容量问题。
? 实现原理，对于大顶堆和小顶堆的实现我们不过多赘述，这里我们主要说一下如何实现的整合和扩容：
? 首先，我们在该数据结构的构造方法中，传入一个max参数，这是一个Boolean类型的参数，当max为true时，创建的堆为大顶堆，当max为FALSE时，创建的堆为小顶堆，因为大顶堆和小顶堆的代码只有在添加元素时调用的上浮up方法和删除元素时调用的下沉down方法中有区别，
分别是，当上浮方法时，需要比较添加元素与其父元素的值，如果添加元素大于父元素，将父元素的值下移到子元素上，子元素指针上浮到父元素继续比较时，堆为大顶堆，反之则为小堆顶，因此在这一步我们只需下面这段三元运算符代码即可切换大/小顶堆：
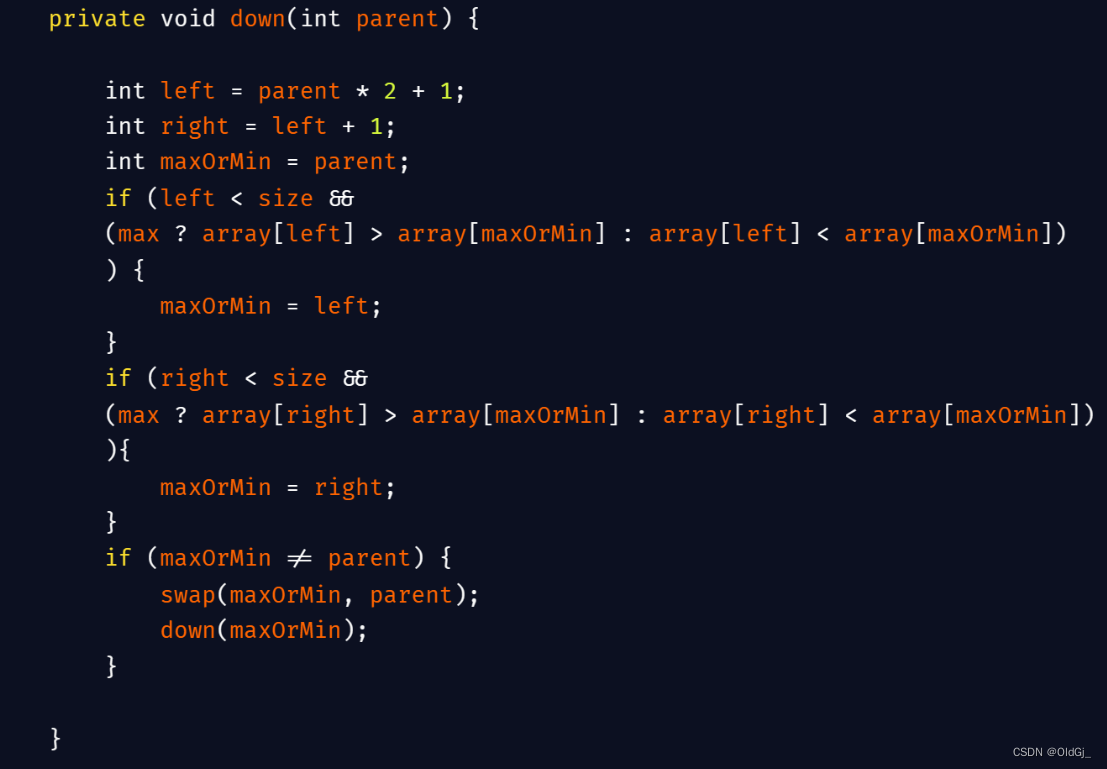
当下沉方法时，我们需要加入下面这段代码：
实现扩容的方法和实现动态数组的方式是相似的，如下：
此方法需要在加入元素的offer方法中，判断如果堆容量满时调用！
2023/12/25
今日数据结构：双锁实现阻塞队列
2023/12/26
每日力扣：215. 数组中的第K个最大元素（堆实现）
给定整数数组
nums和整数k，请返回数组中第**k**个最大的元素。请注意，你需要找的是数组排序后的第
k个最大的元素，而不是第k个不同的元素。你必须设计并实现时间复杂度为
O(n)的算法解决此问题。示例 1:
输入: [3,2,1,5,6,4], k = 2 输出: 5示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4 输出: 4提示：
1 <= k <= nums.length <= 105-104 <= nums[i] <= 104
小顶堆：
public int findKthLargest(int[] nums, int k) {
MinHeap heap = new MinHeap(k);
for (int i = 0; i < k; i++) {
heap.offer(nums[i]);
}
for (int i = k; i < nums.length; i++) {
if (nums[i] > heap.peek()) {
heap.replace(nums[i]);
}
}
return heap.peek();
}
这段 Java 代码定义了一个名为
findKthLargest的方法，该方法接受一个整数数组nums和一个整数k作为输入，并返回数组中第k大的整数。该方法使用一个小顶堆数据结构来高效地找到数组中的第k大元素。
- 初始化一个具有
k容量的小顶堆。这个最小顶堆存储输入数组中的前k个最大元素。- 遍历输入数组的前
k个元素，并将它们添加到最小堆中。- 然后遍历输入数组中剩余的元素。如果一个元素大于最小堆中的最小元素，则用该元素替换最小堆中的最小元素。
- 遍历完所有输入数组元素后，方法返回小顶堆中的最小元素，即数组中的第
k大元素。小顶堆数据结构是一个二叉堆数据结构，其中每个元素的子元素存储在一个较低级别的数组中。在最小堆中，父元素总是小于其子元素。
findKthLargest方法充分使用了小顶堆的这种性质，可以在 O(n log k) 的时间复杂度内找到输入数组中的第k大元素，其中 n 是输入数组的长度。
2023/12/27
每日力扣：703. 数据流中的第 K 大元素
设计一个找到数据流中第
k大元素的类（class）。注意是排序后的第k大元素，不是第k个不同的元素。请实现
KthLargest类：
KthLargest(int k, int[] nums)使用整数k和整数流nums初始化对象。int add(int val)将val插入数据流nums后，返回当前数据流中第k大的元素。示例：
输入： ["KthLargest", "add", "add", "add", "add", "add"] [[3, [4, 5, 8, 2]], [3], [5], [10], [9], [4]] 输出： [null, 4, 5, 5, 8, 8] 解释： KthLargest kthLargest = new KthLargest(3, [4, 5, 8, 2]); kthLargest.add(3); // return 4 kthLargest.add(5); // return 5 kthLargest.add(10); // return 5 kthLargest.add(9); // return 8 kthLargest.add(4); // return 8提示：
1 <= k <= 104
0 <= nums.length <= 104
-104 <= nums[i] <= 104
-104 <= val <= 104最多调用
add方法104次题目数据保证，在查找第
k大元素时，数组中至少有k个元素
方法一：小顶堆
public class KthLargest {
private MinHeap heap;
public KthLargest(int k, int[] nums) {
heap = new MinHeap(k);
for (int num : nums) {
add(num);
}
}
public int add(int val) {
if (!heap.isFull()) {
heap.offer(val);
} else if (val > heap.peek()) {
heap.replace(val);
}
return heap.peek();
}
}
/**
* 小顶堆
*/
public class MinHeap {
private final int[] array;
private int size;
public MinHeap(int capacity) {
array = new int[capacity];
}
/**
* 如果传入一个普通数组，要执行建堆操作，将当前数组转换为堆数组
*/
public MinHeap(int[] array) {
this.array = array;
this.size = array.length;
heapify();
}
/**
* 返回堆顶元素
*/
public Integer peek() {
if(isEmpty()){
return null;
}
return array[0];
}
/**
* 删除堆顶元素
*/
public Integer poll() {
if(isEmpty()){
return null;
}
/*
1.先记录当前堆顶元素，方便返回结果值
2.将堆顶元素与堆中最后一个元素交换
3.删除最后一个元素
4.将推顶元素进行下潜down操作
*/
int top = array[0];
swap(0, size - 1);
size--;
down(0);
return top;
}
/**
* 删除指定索引位置的元素
*/
public Integer poll(int index) {
if(isEmpty()){
return null;
}
int deleted = array[index];
swap(index, size - 1);
size--;
down(index);
return deleted;
}
/**
* 替换堆顶元素
*/
public boolean replace(int replaced) {
if(isEmpty()){
return false;
}
array[0] = replaced;
down(0);
return true;
}
/**
* 向推中添加元素
*/
public boolean offer(int offered) {
if(isFull()){
return false;
}
/*
1.判断推是否已满
2.调用上浮up方法，将待添加元素加入到堆中合适位置
3.堆元素个数size ＋ 1
*/
up(offered, size);
size++;
return true;
}
/**
* 上浮
* @param offered 待添加元素值
* @param index 向哪个索引位置添加
*/
private void up(int offered, int index) {
/*
1.记录孩子的索引位置
2.通过孩子的索引找到父亲的索引位置 公式： parent = (child - 1) / 2;
3.比较添加元素与其父亲节点元素的值
4.如果添加元素小于父亲节点元素的值，将父亲节点元素的值下移，如果大于，则直接在孩子索引位置插入元素
5.将孩子索引指向其父亲索引
6.循环操作 2,3,4,5 直到孩子索引为推顶索引0，或者添加元素大于父亲节点元素的值
*/
int child = index;
while (child > 0) {
int parent = (child - 1) >> 1;
if (offered < array[parent]) {
array[child] = array[parent];
} else {
break;
}
child = parent;
}
array[child] = offered;
}
/**
* 建推
*/
public void heapify() {
/*
1.找到完全二叉树的最后一个非叶子节点 公式： size / 2 - 1
2.从后向前，依次对每个飞非叶子节点调用下潜down方法
*/
for (int i = (size >> 1) - 1; i >= 0; i--) {
down(i);
}
}
/**
* 下潜
*/
private void down(int parent) {
/*
1.找到当前节点的左孩子节点和右孩子节点
2.将当前节点的值和左孩子，右孩子的值进行比较
3.定义一个变量min，用于存放当前节点与其左右孩子中最小的值的下标
4.默认最小值先为当前节点，如果左孩子的值小于当前节点，更新min指针为左孩子下标，右孩子类似
5.如果min指针不等于当前节点的下标（左右孩子中有小于当前节点的值），交换当前节点与min下标对应 节点的值，递归调用下潜down方法，将原节点继续下潜
*/
int left = parent * 2 + 1;
int right = left + 1;
int min = parent;
if (left < size && array[left] < array[min]) {
min = left;
}
if (right < size && array[right] < array[min]) {
min = right;
}
if (min != parent) {
swap(min, parent);
down(min);
}
}
/**
* 交换
*/
private void swap(int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
}
/**
* 判空
*/
public boolean isEmpty() {
return size == 0;
}
/**
* 判满
*/
public boolean isFull() {
return size == array.length;
}
}
这段 Java 代码定义了一个名为
KthLargest的类，该类包含一个构造函数和一个名为add的方法。该类使用了一个名为heap的最小堆对象来存储输入数组中的前k个最大元素。
- 构造函数接受两个参数：整数
k和整数数组nums。它初始化一个具有k容量的小顶堆对象heap，并将输入数组中的所有元素添加到最小堆中。add方法接受一个整数val作为输入。该方法首先检查最小堆是否已满。如果小顶堆未满，则将val添加到最小堆中。如果最小堆已满且val大于最小堆中的最小元素，则用val替换最小堆中的最小元素。- 最后，
add方法返回最小堆中的最小元素，即数组中的第k大元素。小顶堆数据结构是一个二叉堆数据结构，其中每个元素的子元素存储在一个较低级别的数组中。在最小堆中，父元素总是小于其子元素。
KthLargest类充分使用了最小堆的这种性质，可以在 O(n log k) 的时间复杂度内找到输入数组中的第k大元素，其中 n 是输入数组的长度。
方法二：优先级队列
class KthLargest {
PriorityQueue<Integer> pq;
int k;
public KthLargest(int k, int[] nums) {
this.k = k;
pq = new PriorityQueue<Integer>();
for (int x : nums) {
add(x);
}
}
public int add(int val) {
pq.offer(val);
if (pq.size() > k) {
pq.poll();
}
return pq.peek();
}
}
方法二：优先队列
我们可以使用一个大小为 k 的优先队列来存储前 k 大的元素，其中优先队列的队头为队列中最小的元素，也就是第 k 大的元素。在单次插入的操作中，我们首先将元素 val 加入到优先队列中。如果此时优先队列的大小大于 k，我们需要将优先队列的队头元素弹出，以保证优先队列的大小为 k。
2023/12/28
力扣每日一刷：295. 数据流的中位数
中位数是有序整数列表中的中间值。如果列表的大小是偶数，则没有中间值，中位数是两个中间值的平均值。
- 例如
arr = [2,3,4]的中位数是3。- 例如
arr = [2,3]的中位数是(2 + 3) / 2 = 2.5。实现 MedianFinder 类:
MedianFinder()初始化MedianFinder对象。void addNum(int num)将数据流中的整数num添加到数据结构中。double findMedian()返回到目前为止所有元素的中位数。与实际答案相差10-5以内的答案将被接受。示例 1：
输入 ["MedianFinder", "addNum", "addNum", "findMedian", "addNum", "findMedian"] [[], [1], [2], [], [3], []] 输出 [null, null, null, 1.5, null, 2.0] 解释 MedianFinder medianFinder = new MedianFinder(); medianFinder.addNum(1); // arr = [1] medianFinder.addNum(2); // arr = [1, 2] medianFinder.findMedian(); // 返回 1.5 ((1 + 2) / 2) medianFinder.addNum(3); // arr[1, 2, 3] medianFinder.findMedian(); // return 2.0提示:
-105 <= num <= 105- 在调用
findMedian之前，数据结构中至少有一个元素- 最多
5 * 104次调用addNum和findMedian
- 使用自定义的堆数据结构实现
class MedianFinder {
private final Heap left;
private final Heap right;
public MedianFinder() {
left = new Heap(10,true);
right = new Heap(10,false);
}
/*
1. 1 3 5 <-> 7 9 10
先将数据流分为上述两部分，其中左边是一个大顶堆，右边是一个小顶堆
两部分在保持个数之差不大于1的情况下，数据流中的中位数就是
如果两部分元素个数相等 = (大顶堆中的堆顶元素+小顶堆中的堆顶元素)/2
如果两部分元素个数不等 = 大顶堆中的堆顶元素（后面讲原因）
问：如何保证两部分元素个数之差不大于1呢？
我们规定,当添加元素时,如果两部分元素个数相等，则将左部分（大顶堆）中个数加一
如果两部分元素个数不相等，则将右部分（小顶堆）中个数加一
问：如何将新元素正确加入到两个堆中呢？
我们规定，如果如果两部分元素个数相等，先将元素加入到右部分，再从右部分中拿出最小的元素加入到左部分
如果两部分元素个数不相等，先将元素加入到左部分，再从左部分中拿出最大的元素加入到右部分
*/
//添加元素
public void addNum(int num) {
if (left.getSize() == right.getSize()) {
right.offer(num);
left.offer(right.poll());
} else {
left.offer(num);
right.offer(left.poll());
}
}
//返回中位数
public double findMedian() {
if (left.getSize() == right.getSize()) {
return (left.peek() + right.peek()) / 2.0;
} else {
return left.peek();
}
}
/**
* 自动扩容 大小堆
*/
static class Heap {
private int[] array;
private int size;
private final Boolean max;
public int getSize() {
return size;
}
public Heap(int capacity, Boolean max) {
array = new int[capacity];
this.max = max;
}
/**
* 如果传入一个普通数组，要执行建堆操作，将当前数组转换为堆数组
*/
public Heap(int[] array, Boolean max) {
this.array = array;
this.size = array.length;
this.max = max;
heapify();
}
/**
* 返回堆顶元素
*/
public Integer peek() {
if (isEmpty()) {
return null;
}
return array[0];
}
/**
* 删除堆顶元素
*/
public Integer poll() {
if (isEmpty()) {
return null;
}
/*
1.先记录当前堆顶元素，方便返回结果值
2.将堆顶元素与堆中最后一个元素交换
3.删除最后一个元素
4.将推顶元素进行下潜down操作
*/
int top = array[0];
swap(0, size - 1);
size--;
down(0);
return top;
}
/**
* 删除指定索引位置的元素
*/
public Integer poll(int index) {
if (isEmpty()) {
return null;
}
int deleted = array[index];
swap(index, size - 1);
size--;
down(index);
return deleted;
}
/**
* 替换堆顶元素
*/
public boolean replace(int replaced) {
if (isEmpty()) {
return false;
}
array[0] = replaced;
down(0);
return true;
}
/**
* 向推中添加元素
*/
public boolean offer(int offered) {
if (isFull()) {
//扩容
grow();
}
/*
1.判断推是否已满
2.调用上浮up方法，将待添加元素加入到堆中合适位置
3.堆元素个数size ＋ 1
*/
up(offered, size);
size++;
return true;
}
/**
* 扩容
*/
private void grow() {
//新建堆容量 原来的1.5倍
int newCapacity = size + (size >> 1);
int[] newArray = new int[newCapacity];
//将旧堆中的数据移入新堆中
System.arraycopy(array,0,newArray,0,size);
//更新旧的堆
array = newArray;
}
/**
* 上浮
*
* @param offered 待添加元素值
* @param index 向哪个索引位置添加
*/
private void up(int offered, int index) {
int child = index;
while (child > 0) {
int parent = (child - 1) / 2;
boolean temp = max ? offered > array[parent] : offered < array[parent];
if (temp) {
array[child] = array[parent];
} else {
break;
}
child = parent;
}
array[child] = offered;
}
/**
* 建推
*/
public void heapify() {
/*
1.找到完全二叉树的最后一个非叶子节点 公式： size / 2 - 1
2.从后向前，依次对每个飞非叶子节点调用下潜down方法
*/
for (int i = (size >> 1) - 1; i >= 0; i--) {
down(i);
}
}
/**
* 下潜
*/
private void down(int parent) {
int left = parent * 2 + 1;
int right = left + 1;
int maxOrMin = parent;
if (left < size &&
(max ? array[left] > array[maxOrMin] : array[left] < array[maxOrMin])){
maxOrMin = left;
}
if (right < size &&
(max ? array[right] > array[maxOrMin] : array[right] < array[maxOrMin])){
maxOrMin = right;
}
if (maxOrMin != parent) {
swap(maxOrMin, parent);
down(maxOrMin);
}
}
/**
* 交换
*/
private void swap(int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
}
/**
* 判空
*/
public boolean isEmpty() {
return size == 0;
}
/**
* 判满
*/
public boolean isFull() {
return size == array.length;
}
}
}
2 . 使用jdk自带的数据结构PriorityQueue实现
使用JDK自带的PriorityQueue实现大顶堆与小顶堆：
? 大顶堆：
PriorityQueue<Integer> maxQue = new PriorityQueue<>((a, b) -> Integer.compare(b, a)); PriorityQueue<Integer> maxQue = new PriorityQueue<>((a, b) -> (a - b));//大顶堆推荐使用? 小顶堆（默认）：
PriorityQueue<Integer> minQue = new PriorityQueue<>((a, b) -> Integer.compare(a, b)); PriorityQueue<Integer> minQue = new PriorityQueue<>((a, b) -> (b - a)); PriorityQueue<Integer> minQue = new PriorityQueue<>(); //小顶堆默认
/**
* 数据流中的中位数
* 使用jdk自带的 PriorityQueue对象实现 大小顶堆
*/
@SuppressWarnings("all")
public class E03Leetcode295_jdk {
private PriorityQueue<Integer> maxQue;
private PriorityQueue<Integer> minQue;
public E03Leetcode295_jdk() {
// 大顶堆
maxQue = new PriorityQueue<>((a, b) -> Integer.compare(b, a));
// maxQue = new PriorityQueue<>((a, b) -> (a - b));
// 小顶堆（默认）
minQue = new PriorityQueue<>((a, b) -> Integer.compare(a, b));
// minQue = new PriorityQueue<>((a, b) -> (b - a));
}
//添加元素
public void addNum(int num) {
if (maxQue.size() == minQue.size()) {
minQue.offer(num);
maxQue.offer(minQue.poll());
} else {
maxQue.offer(num);
minQue.offer(maxQue.poll());
}
}
//返回中位数
public double findMedian() {
if (maxQue.size() == minQue.size()) {
return (maxQue.peek() + minQue.peek()) / 2.0;
} else {
return maxQue.peek();
}
}
}
2023/12/29
今日数据结构：动态 大/小 顶堆
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- ABB PEBBR6 2UBA004416R0006 变 频 器工作手册参详
- 代码随想录算法训练营Day20|654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
- C语言-＞动态内存管理
- 每日一道算法题 12（2023-12-20）
- 说说你对promise的理解
- oracle23安装并 配置内网代理（安装nginx oracle23）
- 如何有效抑制DCDC电源纹波？
- 【Android 13】使用Android Studio调试系统应用之Settings移植（一）：编译服务器的配置、AOSP源码的下载、编译、运行
- 优惠券兑换码生成需求——事务同步回调问题分析
- 如何用二维码看视频？视频做成二维码的快捷教程