【长文阅读】MAMBA作者博士论文＜MODELING SEQUENCES WITH STRUCTURED STATE SPACES＞-Chapter1

Gu A. Modeling Sequences with Structured State Spaces[D]. Stanford University, 2023.

本文是MAMBA作者的博士毕业论文，为了理清楚MAMBA专门花时间拜读这篇长达330页的博士论文，由于知识水平有限，只能尽自己所能概述记录，并适当补充一些相关数学背景，欢迎探讨与批评指正。内容多，分章节更新以免凌乱，等更新完毕补充目录跳转链接。

Abstract

这篇文档的摘要介绍了在机器学习领域的显著进步，特别是在序列模型方面，这些模型对深度学习在各种科学应用中的成功至关重要。尽管目前的方法取得了成功，但它们在处理复杂的序列数据（如涉及长期依赖性的数据）时存在限制，例如需要大量的特定任务专业化、计算效率低下等问题。为了解决这些问题，论文介绍了一种使用状态空间模型的新方法。这些模型灵活、理论基础扎实、计算效率高，并且在多种数据类型和应用中表现出色。它们扩展了标准深度序列模型（如循环神经网络和卷积神经网络）的功能。论文还开发了适用于现代硬件的新型结构化状态空间，适合长序列处理和其他场景，如自回归推理。此外，它还提出了一种用于逐步建模连续信号的新数学框架，通过这种框架，可以为状态空间模型提供原理上的状态表示，并改善其处理长期依赖性的能力。这种新方法为机器学习提供了有效且多功能的工具，特别是在处理大规模的一般序列数据方面。

1.Introduction

1.1 Deep Sequence Models

首先定义了序列模型，一张图就把CNN 、RNN、Transformer以及本文的模型概括进去。

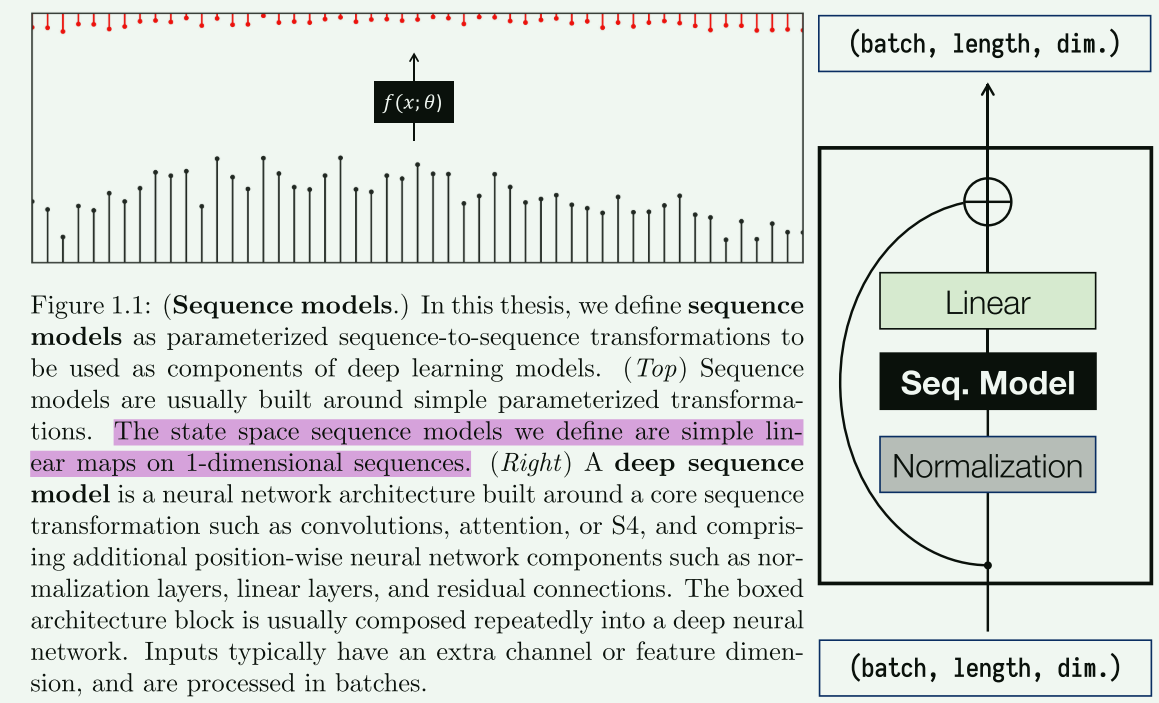
在本文中，将序列模型定义为参数化序列到序列的转换，用作深度学习模型的组件。 （上）序列模型通常围绕简单的参数化转换构建。定义的状态空间序列模型是一维序列上的简单线性映射。 （右）深度序列模型是一种围绕核心序列变换（例如卷积、注意力或 S4）构建的神经网络架构，并包含附加的位置神经网络组件，例如归一化层、线性层和残差连接。盒装架构块通常被重复组成深度神经网络。输入通常具有额外的通道或特征维度，并且是批量处理的。

深度学习模型用于序列数据的处理被描述为基于简单机制（如递归、卷积或注意力机制）的序列到序列的转换。这些基本元素被整合进标准的深度神经网络架构，形成了主要的深度序列模型家族：循环神经网络（RNNs）、卷积神经网络（CNNs）和Transformers。这些模型通过标准深度学习技术（如梯度下降的反向传播）实现了强大的参数化转换。

每种模型家族都在机器学习领域取得了巨大成功，例如RNNs在机器翻译中的应用、CNNs成为首个神经音频生成模型，以及Transformers在自然语言处理领域的革命性影响。然而，这些模型也有其固有的权衡。例如，

• RNNs是一种自然的、状态驱动的序列数据模型，它们在训练过程中较慢，并且存在优化困难（如“梯度消失问题”），限制了它们处理长序列的能力。
• CNNs擅长处理本地上下文和编码属性（如平移等变性），训练速度快，但在序列推理上成本较高，且存在上下文长度的固有限制。
• Transformers凭借处理长程依赖性和并行化的能力取得了巨大成功，但它们在序列长度上的处理呈二次方规模增长。
• 神经微分方程（NDEs），这是一种原理性的数学模型，理论上可以处理连续时间问题和长期依赖关系，但效率非常低。

这些权衡指出了深度序列模型面临的三个广泛挑战：

1. 通用性能力：深度学习的一个广泛目标是开发可以广泛应用于各种问题的通用构建模块。序列模型为解决许多问题提供了一个通用框架，减少了专门化的需求，因为它们可以应用于任何可以被视为序列的设置。
2. 计算效率：实际应用深度序列模型需要计算它们定义的函数（即参数化的序列到序列的映射），这可能在训练和推理时面临挑战。
3. 长程依赖性：实际世界的序列数据可能需要对成千上万的时间步进行推理。除了处理长输入所需的计算问题外，还需要能够模拟这种长程依赖性中的复杂交互。

尽管为长程依赖性设计的解决方案，但在像Long Range Arena这样的挑战性基准测试中，这些解决方案仍然表现不佳。

1.2 State Space Sequence Models

本文介绍了一系列基于线性状态空间模型（SSM）的新的深度序列模型。将这个 SSM 定义为一个简单的序列模型，它通过隐式潜在状态$x(t)\in {\mathbb{R}}^N$映射一维函数或序列 $u(t)\in \mathbb{R}?y(t)\in \mathbb{R}$

$\begin{array}{rl}{x}^{\prime }(t)& =\mathbf{A}x(t)+\mathbf{B}u(t)\\ y(t)& =\mathbf{C}x(t)+\mathbf{D}u(t)\end{array}$

这些模型将一维函数或序列通过隐含的潜在状态映射到另一个序列，形成了一种简单的序列模型。SSMs在控制理论、计算神经科学、信号处理等领域都是基础性的科学模型，它们模拟了潜变量在状态空间中的演变，并且通常定义了这些动态的概率模型。

状态空间模型与如NDEs、RNNs和CNNs等其他模型家族有紧密关联，可以以多种形式表达，以获得通常需要专门模型的不同能力。SSMs具有以下特性：

1. SSMs是连续的：它们本身是微分方程，可以模拟连续时间模型的独特应用，如模拟连续过程、处理缺失数据和适应不同的采样率。
2. SSMs是递归的：它们可以被离散化成线性递归，用标准技术模拟推理时的状态驱动递归模型，每个时间步骤具有恒定的内存和计算量。
3. SSMs是卷积的：它们是线性时不变系统，已知可以显式表示为连续卷积。此外，离散时间版本可以在训练期间使用离散卷积进行并行化，从而提高训练效率。

然而，SSMs的通用性也带来了一些权衡。简单的SSMs仍然面临其他挑战，如速度远慢于同等大小的RNNs和CNNs，以及难以记住长期依赖性，例如继承了RNNs的梯度消失问题。

为了解决这些挑战，引入了具有结构化状态空间（S4）的新算法和理论。这些算法通过在状态矩阵A上施加结构，以适应高效的算法。S4模型的第一个结构使用状态矩阵的对角线参数化，非常简单且足以表示几乎所有SSMs。然后，通过允许低秩修正项，可以表示一类特殊的SSMs。综合了多种技术思想，如生成函数、线性代数变换和结构化矩阵乘法的结果，开发了这些结构的算法，时间复杂度和空间复杂度均为O?(N + L)，这对于序列模型来说是非常紧凑的。

此外，SSMs在处理长期依赖性方面表现不佳，这是由于线性一阶常微分方程解决为指数函数，可能导致序列长度中梯度指数级缩放。为了解决这个问题，开发了一个称为HIPPO的数学框架，用于在线函数逼近（或记忆）。HIPPO产生的方法旨在通过维护其历史的压缩来增量记忆连续函数。这些方法实际上是SSMs的特定形式，尽管它们是完全独立地激发出来的。