密码学：一文读懂非对称密码体制

前言

花十分钟阅读完这篇文章，你将对密码学中大名鼎鼎的非对称密码体制有个整体的理解和把握。
对整体的框架有所了解之后，再去看RSA，散列函数、数字证书、单双向认证等等这些密码学的知识，或者去开发安全相关的项目开发就不会迷路，能找到正确的方向。

上篇讲述关于对称加密体系的博文一度被推上热榜，说明应该是能帮助到一些朋友的。今天来介绍下作为对称密码体制的补充：非对称密码体制。

对于对称密钥体系不了解的朋友可以翻看：密码学：一文读懂对称密钥体系

下面开始正文：

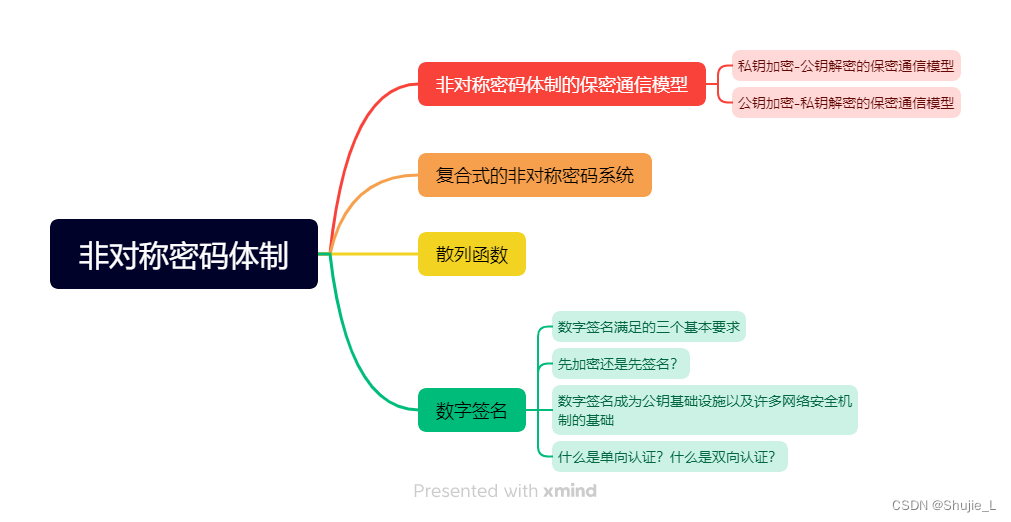
非对称密码体制的保密通信模型

非对称密码体制的保密通信模型如图所示。非对称密码体制与对称密码体制相对，其主要的区别在于，非对称密码体制的加密密钥和解密密钥不相同，分为两个密钥，一个公开，一个保密。公开的密钥称为公钥，保密的密钥称为私钥。因此非对称密码体制也称为公钥密码体制。非对称密码体制使得发送者和接收者无密钥传输的保密通信成为可能，弥补了对称密码体制的缺陷。

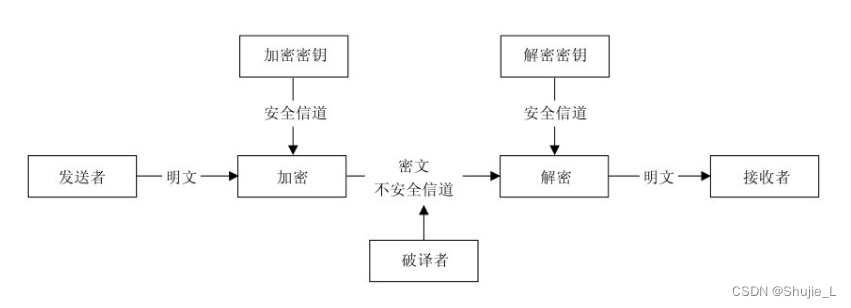
在非对称密码体制中，公钥和私钥均可用于加密与解密操作，但它与对称密码体制有极大的不同。公钥与私钥分属通信双方，一份消息的加密与解密需要公钥与私钥共同参与。公钥加密则需要私钥解密，反之，私钥加密则需要公钥解密。

我们把通信双方定义为甲乙两方，甲乙两方分场景扮演信息发送者或接收者。公钥与私钥分属甲乙两方，甲方拥有私钥，乙方拥有公钥。

为了更好地描述非对称密码体制通信流程，我们通过图片来说明甲乙双方如何完成一次完整的会话。

私钥加密-公钥解密的保密通信模型

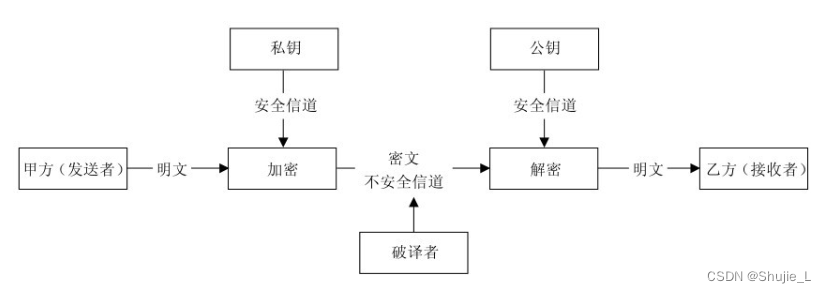
公钥加密-私钥解密的保密通信模型

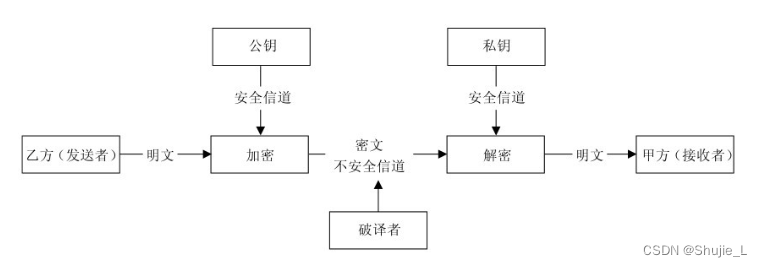
非对称密码体制的主要优点是可以适应开放性的使用环境，密钥管理问题相对简单，可以方便、安全地实现数字签名和验证。

RSA是非对称密码体制的典范，它不仅可以完成一般的数据保密操作，同时它也支持数字签名与验证。除了数字签名，非对称密码体制还支持数字信封等技术。

非对称密码算法的安全性完全依赖于基于计算复杂度上的难题，通常来自于数论例如：
RSA源于整数因子分解问题。
DSA(数字签名算法)源于离散对数问题。
ECC(圆曲线加密算法)源于离散对数问题。

复合式的非对称密码系统

由于这些数学难题的实现多涉及底层模数乘法或指数运算，相对于分组密码需要更多的计算资源。为了弥补这一缺陷，非对称密码系统通常是复合式的。用高效率的对称密码算法对信息进行加密解密处理，用非对称密钥加密对称密码系统所使用的密钥。通过结合对称密码和非对称密码的优势，以提高整体系统的效率和安全性。

对称密码算法更高效： 对称密码算法在加密和解密过程中使用相同的密钥，因此通常比非对称密码算法更快。对称密码算法对数据进行加密和解密的速度很快，因为操作只涉及简单的数学运算，例如替换、置换和异或操作。

非对称密码算法更安全： 非对称密码算法提供了更高的安全性，因为它涉及到两个密钥：公钥和私钥。信息可以使用公钥加密，但只有拥有相应私钥的实体才能解密。这种体系结构解决了密钥分发和管理的问题，但由于计算复杂度较高，不适合对大量数据进行直接加密和解密。

为了克服对称密码算法和非对称密码算法各自的缺点，通常采用复合式的方法。具体而言，可以使用对称密码算法来对大量数据进行高效的加密和解密操作，而非对称密码算法则用于安全地传输和管理对称密码算法所使用的密钥。

这种复合方式的好处在于，对称密码算法提供了高效性，而非对称密码算法增加了系统的安全性。通过使用非对称密钥对对称密钥进行加密，可以确保在密钥传输过程中的安全性，同时仍然能够利用对称密码算法的高效性。这种组合可以在实际应用中平衡安全性和性能需求。

散列函数

曾经提到过对于信息完整性验证需要其在讲到对称密码体制的流密码实现方式时，他技术来支持，这种技术就是由散列函数提供的消息认证技术。
散列函数，也称做哈希函数、消息摘要函数、单向函数或杂凑函数。与上述密码体制不同的是，散列函数的主要作用不是完成数据加密与解密的工作，它是用来验证数据的完整性的重要技术。通过散列函数，可以为数据创建“数字指纹” (散列值)。散列值通常是一个短的随机字母和数字组成的字符串。

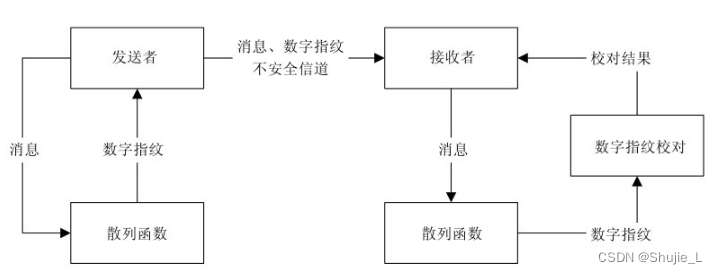
在上述认证流程中，信息收发双方在通信前已经商定了具体的散列算法，并且该算法是公开的。如果消息在传递过程中被篡改，则该消息不能与已获得的数字指纹相匹配。

散列函数具有以下一些特性：

• 消息的长度不受限制

• 对于给定的消息，其散列值的计算是很容易的。

• 如果两个散列值不相同，则这两个散列值的原始输入消息也不相同，这个特性使得散列函数具有确定性的结果

• 散列函数的运算过程是不可逆的，这个特性称为函数的单向性。这也是单向函数命名的由来

• 对于一个已知的消息及其散列值，要找到另一个消息使其获得相同的散列值是不可能的，这个特性称为抗弱碰撞性。这被用来防止伪造

• 任意两个不同的消息的散列值一定不同，这个特性称为抗强碰撞性

散列函数广泛用于信息完整性的验证，是数据签名的核心技术。散列函数的常用算法有MD一消息摘要算法、SHA一安全散列算法及MAC一消息认证码算法。

数字签名

通过散列函数可以确保数据内容的完整性，但这还远远不够。此外，还需要确保数据来源的可认证(鉴别)性和数据发送行为的不可否认性。

完整性、认证性和不可否认性，正是数字签名的主要特征。

数字签名针对以数字形式存储的消息进行处理，产生一种带有操作者身份信息的编码。

执行数字签名的实体称为签名者，签名过程中所使用的算法称为签名算法 (Signature Algorithm) ，签名操作中生成的编码称为签名者对该消息的数字签名。

发送者通过网络将消息连同其数字签名一起发送给接收者。接收者在得到该消息及其数字签名后，可以通过一个算法来验证签名的真伪以及识别相应的签名者。这一过程称为验证过程，其过程中使用的算法称为验证算法 (Verification Algorithm)，执行验证的实体称为验证者。

数字签名离不开非对称密码体制，签名算法受私钥控制，且由签名者保密，验证算法受公钥控制，且对外公开。

RSA算法则既是最为常用的非对称加密算法，也是最为常用的签名算法。DSA算法是典型的数字签名算法，虽然本身属于非对称加密算法不具备数据加密与解密的功能。

数字签名满足的三个基本要求

• 签名者任何时候多无法否认自己曾经签发的数字签名。
• 信息接收者能够验证和确认收到的数字签名，但任何人无法伪造信息发送者的数字签名。
• 当收发双方对数字签名的真伪产生争议时，通过仲裁机构 (可信赖的第三方)进行仲裁

数字签名认证流程如图所示。在这里提请大家注意: 私钥用于签名，公钥用于验证。签名操作只能由私钥完成，验证操作只能有公钥完成，公钥与私钥成对出现，用公钥加密的消息只能用私钥解密，用私钥加密的消息只能用公钥解密。

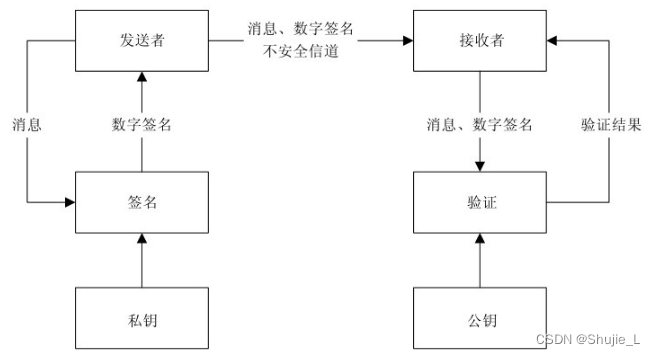
先加密还是先签名？

当然，我们可以对消息先加密，然后对加密后的消息做签名处理，这样乙方获得消息后，先做验证处理，如果验证通过则对消息解密。反之，验证失败则抛弃消息。这样做显然可以提高系统的处理速度，但即便如此，作者仍建议大家对消息先做签名，再做加密处理。加密与签名都应该只针对原始消息 (明文) 做处理。加密是为了确保消息在传送过程中避免被破解，签名是为了确保消息的有效性。消息本身可能就是一个可执行的文件，消息的接收方通过对消息的验证来判别该文件是否有权执行，而这个文件本身是不需要加密的。

数字签名成为公钥基础设施以及许多网络安全机制的基础

由于签名不可伪造，甲方不能否认自己已发送的消息，而乙方可验证消息的来源以及消息是否完整。数字签名可提供OSI参考模型五类安全服务中的三种服务: 认证(鉴别)服务、抗否认服务和数据完整性服务。正因如此，数字签名成为公钥基础设施以及许多网络安全机制的基础。

什么是单向认证？什么是双向认证？

在上述认证过程的描述中，似乎大家有这样一个疑问: 当乙方作为发送方，通过公钥将消息加密后发送给甲方时，由于算法、公钥公开，任何一个已获得公钥的窃听者都可以截获乙方发送的消息，替换成自己的消息发送给甲方，而甲方无法辨别消息是否来源于乙方。也就是说，上述的认证方式是单向的，属于单向认证。如果有两套公私钥，甲乙两方都对数据做签名及验证就可以避免这一问题。没错，这种认证方式正是双向认证。以网银交易为例，一般的网银交易使用的都是单向认证方式，无法验证使用者的身份，而要求较高的网银交易则都是双向认证方式，交易双方身份都可以得到验证。

总结和回顾

从密码体制上划分，现代密码学共分为两种密码体制：对称密码体制和非对称密码体制。对称与非对称的差别源于加密密钥和解密密钥是否对称，即加密密钥与解密密钥是否相同 (对称)。
在对称密码体制中，加密与解密操作使用相同的密钥，我们把这个密钥称为秘密究钥。DES、AES算法都是常用的对称密码算法。流密码和分组密码都属于对称密码体制。流密码实现简单，对环境要求低，适用于手机平台的加密，广泛应用于军事、外交领域。RC4算法就是典型的流密码算法。流密码的理论、算法受限于国家安全因素未能公布。分组密码在这一点上与流密码恰恰相反，其理论、算法公开分类众多。DES、AES算法等主要的对称密码算法均属于分组密码。分组密码共有五种工作模式:电子密码本模式 (ECB) 、密文链接模式 (CBC) 、密文反馈模式(CFB) 、输出反馈模式 (OFB) 、计数器模式 (CTR) 。分组密码会产生短块，关于短块的处理方法有填充法、流密码加密法、密文挪用技术。

在非对称密码体制中，加密与解密操作使用不同的密钥。对外公开的密钥，称为公钥；对外保密的密钥，称为私钥。用公钥加密的数据，只能用私钥解密，反之，用私钥加密的数据，只能用公钥解密。RSA算法是常用的非对称密码算法。非对称密码体制同时支持数字签名技术，如RSA、DSA都是常用的数字签名算法。

散列函数可以有效地确保数据完整性，被作为消息认证技术。常用的散列函数算注有MD5、SHA、MAC。散列函数也是数字签名技术中最重要的技术环节。

数字签名离不开非对称密码体制，其私钥用于签名，公钥用于验证。基于数字签名的不伪造性，数字签名技术成为五类安全服务中数据完整性服务、认证性服务和抗否议性服务的核心技术。通信双方只有一方提供数字签名的认证方式称为单向认证，通信双方都提供数字签名的认证方式称为双向认证。一般网银系统多采用单向认证式，而要求较高的网银交易则都采用双向认证方式。密码学在不断地向前发展，只不过它的发展通常是以其密码算法的破解而引发，以更高安全系数算法的诞生而段落，密码学的明天将无可限量。

参考

《Java加密和解密的艺术》