622.设计循环队列（附带源码）

目录

一、题目

?编辑二、思路

第一种实现方式：数组

1、rear初始化为-1：

2、rear初始化为0：

第二种实现方式：链表

三、源码

---

一、题目

622. 设计循环队列 - 力扣（LeetCode）

二、思路

循环队列，就是头尾相接，很简单。

有两种实现方式，一种是数组，一种是使用链表来实现

我们来逐个分析。

第一种实现方式：数组

这是空队列的情况

我们插入数据：

这个时候，我们的队列尾rear有两种选择，一个是初始的rear置为-1，一个是置为0

1、rear初始化为-1：

如果我们rear初始化为-1，那么，当插入一个数据的时候，front == rear ==0

而明显的此时front == rear 队列不为空：

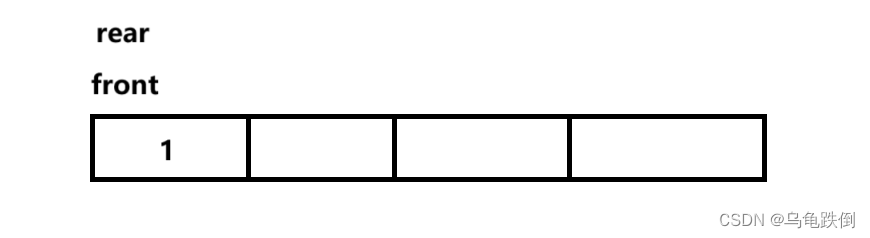
那么，问题来了，什么时候队列为空？

你可能会说，当rear为-1的时候为空，

这样吗？

很明显，也不为空。

这就麻烦了，很操蛋，再分析下去会感觉很难受，因为不仅要判空，还要判满，这也是一个问题。

我们这里不再继续深入分析，如果你有兴趣，可以自己继续分析。

既然比较难受，那么我们换个初始化方式

2、rear初始化为0：

此时的情况是：

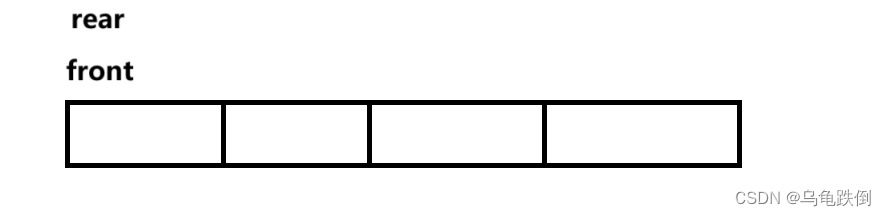
此时front == rear为空，ok，没有问题，那么队列满呢？

????????

卧槽，循环队列rear最后会回到数组前面，此时front也等于rear，冲突了。

怎么办？

很明显，在当前场景下，所用的数组结构有着明显的致命缺陷，使得我们解决问题的成本大大提高

所以，既然此路不通，我们能不能换一个结构？或者说，改造一下这个结构？

很简单，我们的数组多加一个位置：我们数据存储K个，但是申请的空间是K+1个

同时，我们如何让rear到达数组最后的时候又回到数组的0索引位置？

也很简单，%K+1即可

一个值%一个比我大的值对我不会有任何影响
比如0，1，2，3，4，%5不会有影响
但是5%5就会变成0，这个可以用来处理数组的越界的问题，十分有用
或者用来处理数组循环的问题，可以让超过的数量回到初始位置

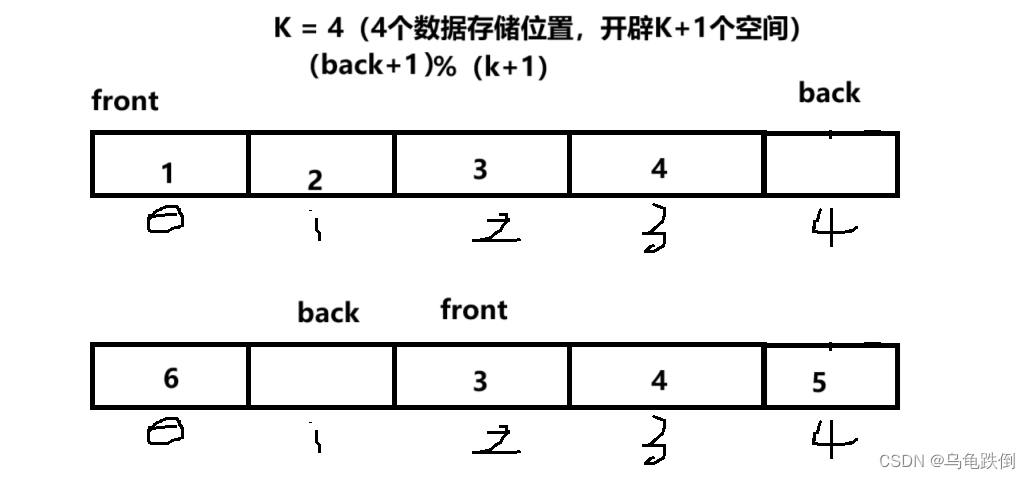
如果不多加一个空间位置，那么当队列为空的时候，front和back相等，当队列满的时候，front和back也相等
那么就无法区分到底是满还是空
为了解决这个问题，我们在数组队列多加了一个位置
这个位置主要用来判断满的问题，当back的下一个位置等于front的时候就是满，
那么和front等于back队列为空就不冲突

注意，我们的rear和front是下标，我们开辟了K+1和空间，那么我们开辟的是数组，数组的最后一个位置的下标是K，当rear指向数组最后一个位置时，rear的值等于最后一个位置的下标，就是K。

事实上，数组判断空和满，也没那么复杂，我们可以多定义一个size记录数组的数据个数，为0就是空，满就是满。很简单，但是实现循环数组也需要一些特殊处理，所以，总的来说，一半一半吧。看你的选择。这里学长选择的是使用多开一个空间，这也是主流的方案，而且听起来也比较高大上不是吗。

第二种实现方式：链表

链表如下：也是多开辟一个空间用于判断空和满

当front等于rear时，为空，当rear->next等于front时为满。很好解决

但是，如果要取尾元素呢？

这就比较麻烦了，你也可以定义双向链表

可是，还有初始化创建链表呢？

最后使用完了销毁链表释放空间呢？

其实也一样的，不同的方案有不同的施行成本，看你自己吧，只要链创建好了，其实也好处理。

三、源码

下面直接上源码：

typedef struct {
    int front;
    int rear;
    int *a;
    int k;
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue *obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a = (int *)malloc(sizeof(int) * (k+1));
    obj->front =0;
    obj->rear = 0;
    obj->k = k;//k个存储数据的位置
    return obj;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->rear == obj->front;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->rear + 1)%(obj->k+1) == obj->front;
}


bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
    {
        return false;
    }
    else
    {
        obj->a[obj->rear] = value;
        obj->rear++;
        obj->rear %= obj->k + 1;
        return true;
    }

}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    {
        return false;
    }
    else
    {
        obj->front++;
        obj->front %= obj->k +1;
        return true;
    }
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    else
        return obj->a[obj->front];
    
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    
        return obj->a[(obj->rear-1 + obj->k + 1)%(obj->k + 1)];
}

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

/**
 * Your MyCircularQueue struct will be instantiated and called as such:
 * MyCircularQueue* obj = myCircularQueueCreate(k);
 * bool param_1 = myCircularQueueEnQueue(obj, value);
 
 * bool param_2 = myCircularQueueDeQueue(obj);
 
 * int param_3 = myCircularQueueFront(obj);
 
 * int param_4 = myCircularQueueRear(obj);
 
 * bool param_5 = myCircularQueueIsEmpty(obj);
 
 * bool param_6 = myCircularQueueIsFull(obj);
 
 * myCircularQueueFree(obj);
*/