python图像二值化处理
目录
图像的二值化处理是将图像上的像素点的灰度值设置为0或255,也就是将整个图像呈现出明显的只有黑和白的视觉效果。二值化是图像分割的一种最简单的方法,可以把灰度图像转换成二值图像。具体实现是将大于某个临界灰度值的像素灰度设为灰度极大值,把小于这个值的像素灰度设为灰度极小值,从而实现二值化。
根据阈值选取的不同,二值化的算法分为固定阈值和自适应阈值。常见的二值化方法有双峰法、P参数法、迭代法和OTSU法等。其中,双峰法是通过寻找直方图上的两个最高峰,将阈值选取在两个峰之间的最低处;P参数法是根据图像的直方图分布情况,动态地确定一个阈值;迭代法是通过多次迭代计算,逐渐逼近最佳的阈值;OTSU法则是通过最大化类间方差来确定最佳阈值。
1、双峰法
双峰法是一种简单的二值化处理方法,其基本思想是找到图像直方图中的两个最大值,并将阈值设定在这两个峰值之间的最低处。这种方法适用于背景和前景差异较大的图像。

import cv2
import numpy as np
def find_peaks(hist):
# 找到直方图中的峰值
peaks = []
for i in range(1, len(hist) - 1):
if hist[i] > hist[i - 1] and hist[i] > hist[i + 1]:
peaks.append(i)
# 返回前两个峰值(如果存在)
if len(peaks) >= 2:
return peaks[0], peaks[1]
else:
return None, None
# 读取图像并转换为灰度图像
image = cv2.imread(r'1.jpg', cv2.IMREAD_GRAYSCALE)
?
# 计算图像的直方图
hist, bins = np.histogram(image.ravel(), 256, [0, 256])
?
# 找到直方图中的两个峰值
peak1, peak2 = find_peaks(hist)
?
# 计算阈值,取两个峰值的平均值作为阈值
threshold = int((peak1 + peak2) / 2)
?
# 对图像进行二值化处理
binary_image = cv2.threshold(image, threshold, 255, cv2.THRESH_BINARY)[1]
?
# 显示二值化后的图像
cv2.imshow('Binary Image', binary_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
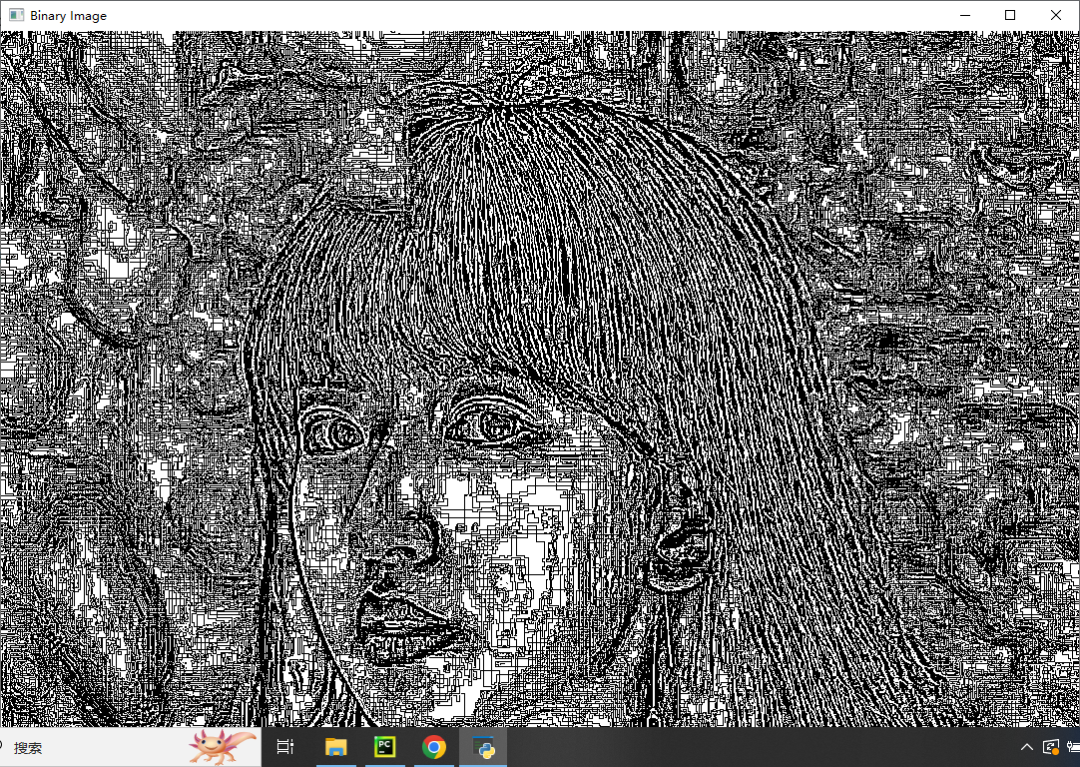
2、P参数法
P参数法是一种图像二值化处理方法,用于将灰度图像转换为二值图像。它基于图像的局部信息进行操作,具体步骤如下:
-
选择一个合适的阈值T(0 ≤ T ≤ 255)作为全局阈值。
-
对于图像中的每个像素点,计算其周围邻域内像素的均值和标准差。如果该像素的灰度值大于等于均值加上参数P乘以标准差,则将其设置为白色(255),否则设置为黑色(0)。

import cv2
import numpy as np
?
def p_thresholding(image, P):
# 将图片转换为灰度图像
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
?
# 获取图像大小
height, width = gray_image.shape
?
# 初始化输出二值图像
binary_image = np.zeros((height, width), np.uint8)
?
for i in range(height):
for j in range(width):
# 计算像素的周围邻域内像素的均值和标准差
neighborhood_mean = np.mean(gray_image[max(0, i-1):min(height, i+2), max(0, j-1):min(width, j+2)])
neighborhood_std = np.std(gray_image[max(0, i-1):min(height, i+2), max(0, j-1):min(width, j+2)])
?
# 根据P参数法判断像素的二值化结果
if gray_image[i, j] >= neighborhood_mean + P * neighborhood_std:
binary_image[i, j] = 255
else:
binary_image[i, j] = 0
?
return binary_image
?
# 读取图像
image = cv2.imread(r'q.jpg')
?
# 设置参数P的值
P = 0.2
?
# 调用P参数法二值化函数
binary_image = p_thresholding(image, P)
?
# 显示原始图像和二值图像
cv2.imshow('Original Image', image)
cv2.imshow('Binary Image', binary_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
?
3、迭代法
基本原理很简单:
(1)选择灰度图的平均值作为初始阈值T0 ;
(2)计算小于等于T0的平均值T1, 和大于T0的平均值T2;
(3)新的阈值为T = (T1 + T2)/ 2;
(4)比较T和T0,若相等,则返回T,即为迭代阈值; 否则 T0 = T,重复(1)-(3)
import cv2
?
def iterative_thresholding(image, threshold=127):
# 初始化二值化结果
binary_image = image.copy()
?
# 迭代更新阈值
prev_threshold = 0
while threshold != prev_threshold:
prev_threshold = threshold
?
# 计算两个区域的平均灰度值
region1_mean = image[image <= threshold].mean()
region2_mean = image[image > threshold].mean()
?
# 更新阈值
threshold = (region1_mean + region2_mean) // 2
?
# 根据新的阈值进行二值化
binary_image[image <= threshold] = 0
binary_image[image > threshold] = 255
?
return binary_image
?
# 读取图像
image = cv2.imread(r'C:\Users\Downloads\q.jpg')
?
# 调用迭代法二值化函数
binary_image = iterative_thresholding(image)
?
# 显示结果
cv2.imshow('Binary Image', binary_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
4、OTSU法
最大类间方差是由日本学者大津(Nobuyuki Otsu)于1979年提出,是一种确定图像二值化分割阈值的算法。算法假设图像像素能够根据全局阈值,被分成背景[background]和目标[objects]两部分。然后,计算该最佳阈值来区分这两类像素,使得两类像素区分度最大。
从大津法的原理上来讲,该方法又称作最大类间方差法,因为按照大津法求得的阈值进行图像二值化分割后,前景与背景图像的类间方差最大。它被认为是图像分割中阈值选取的最佳算法,计算简单,不受图像亮度和对比度的影响,因此在数字图像处理上得到了广泛的应用。因方差是灰度分布均匀性的一种度量,背景和前景之间的类间方差越大,说明构成图像的两部分的差别越大,当部分前景错分为背景或部分背景错分为前景都会导致两部分差别变小。因此,使类间方差最大的分割意味着错分概率最小。
import cv2
?
# 读取图像并转换为灰度图像
image = cv2.imread(r'q.jpg', cv2.IMREAD_GRAYSCALE)
?
# 使用OTSU法计算最佳阈值
ret, binary_image = cv2.threshold(image, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)
# 显示二值化后的图像
cv2.imshow('Binary Image', binary_image)
cv2.waitKey(0)
cv2.destroyAllWindows()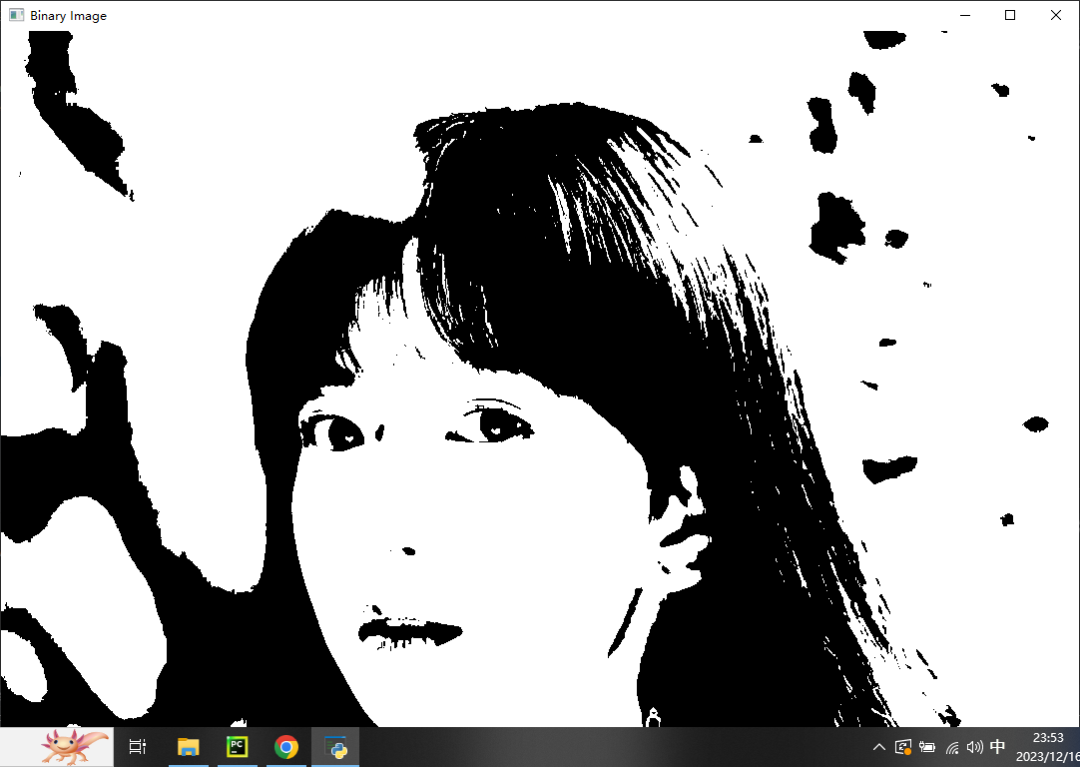
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- MySQL数据库SQL优化详解
- 性能测试能力提升 —— 线程、并发、吞吐量、TPS、QPS、响应时间
- Java刷题篇——LeetCode118. 杨辉三角
- 【HarmonyOS】【应用开发】动画-属性动画基础
- windows系统安装docker
- 基于ssm的社区流浪动物救助领养系统的设计与开发+vue论文
- Javascript 日期对象简介
- 训练营第四十三天 | ● 1049. 最后一块石头的重量 II ● 494. 目标和 ● 474.一和零
- 【DevOps 工具链】搭建 项目管理软件 禅道
- Java中,字符串常量池利用享元模式的原理实现了字符串对象的高效管理和重用