实时阴影技术(Shadow Mapping)
一、Shadow Mapping 概述
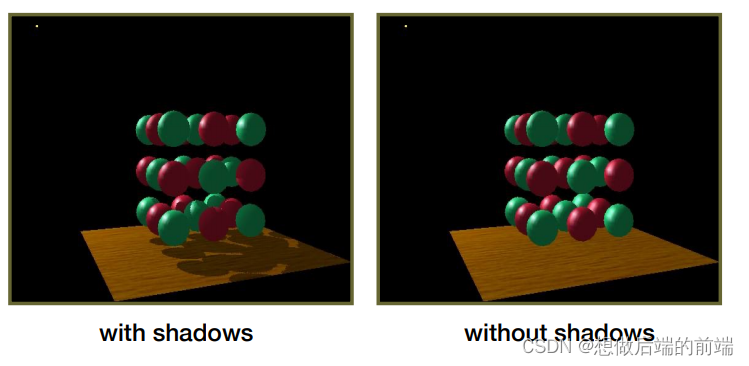
Shadow Mapping 基本原理:
1.1 阴影生成 Pass:
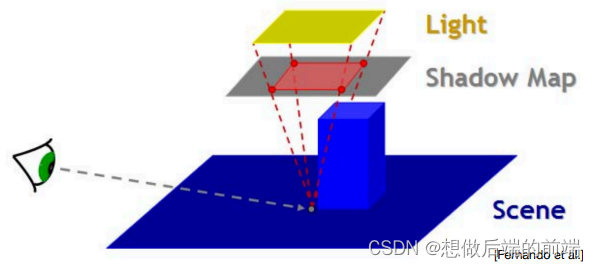
- 额外设置一个摄像机在光源位置(Light Camera,光源摄像机),并且朝光照方向看去。
- 用一张 Texture(称为 阴影贴图 Shadow Map)来记录 Light Camera所看到的像素深度(每个像素位置只记录所见最近深度,而不用做别的 shading 计算)来作为遮挡深度。
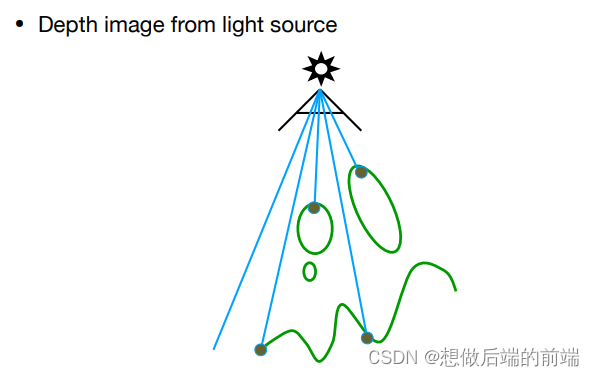
如图,Shadow Map 记录了 Light Camera 所看到的最近深度图,颜色越深,离摄像机越近:

1.2 渲染 Pass
- 主摄像机需要渲染屏幕每个像素时,该像素对应的世界坐标进行 Light Camera 的MVP变换后能得到在 Light Camera屏幕空间中的对应位置 shadowCoord(x’,y’,z’)?
- Shadow Map 里用(x’,y’)采样得到的遮挡深度depth与深度值z’作比较:若depth < z’(意味着像素被光遮挡),这时就可以对该像素降低可见度(Visibility)。
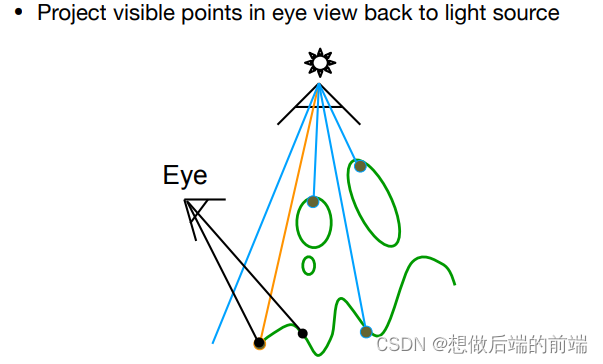
如图为主摄像机每个像素经过变换后比较深度的结果,其中绿色点意味着深度 depth ≈ z’(没有遮挡光照),非绿色点意味着depth < z’(被遮挡了光照)

1.3 Shadow Bias
直接使用Shadow Map可能会在不应该出现阴影的位置出现一些黑白条纹相间的现象(称为 Shadow Acne):
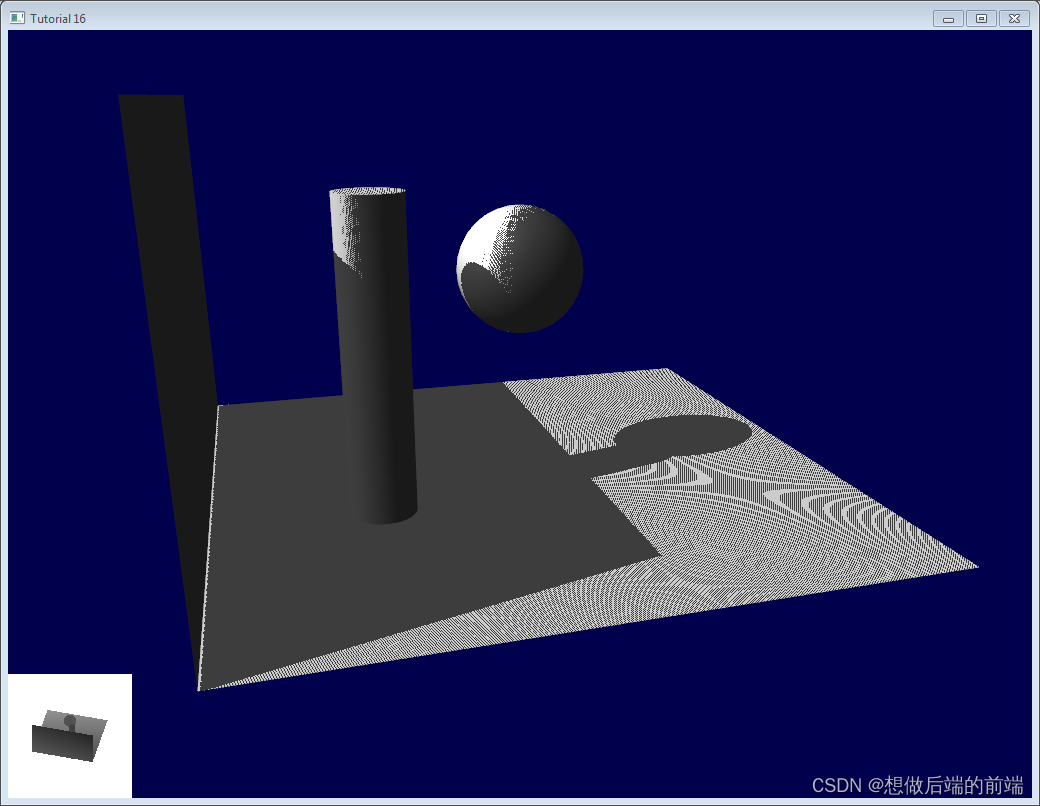
其本质原因在于,Shadow Map 是一个二维数组,离散的存储方式很难完全表示实际的几何信息。尤其当光照方向不垂直于平面时,遮挡深度的采样会和实际深度产生偏差(如图一个不受遮挡的几何平面,但黑色加粗部分却被Shadow Mapping方法认为是被遮挡的):
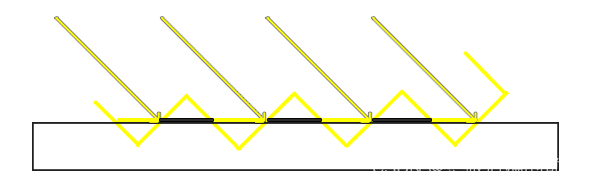
解决方法:直接给采样阴影深度加一个 偏移量 Bias(相当于把阴影深度往远处加,从而更不容易产生遮挡)。
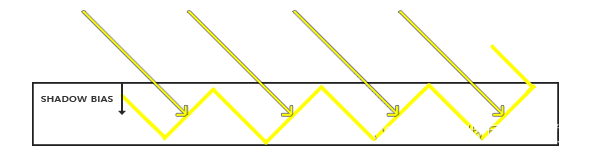

1.4 Peter Panning 问题
然而由于增加了Bias,可能会导致 Peter Panning 现象:往往在物体缝隙间发生漏光。

解决方法: 避免使用单薄的几何体(例如薄墙、薄地面);只要几何体厚度大于Bias,影子边界便会产生在几何体内部,从而不易看见影子与几何体的分离现象。
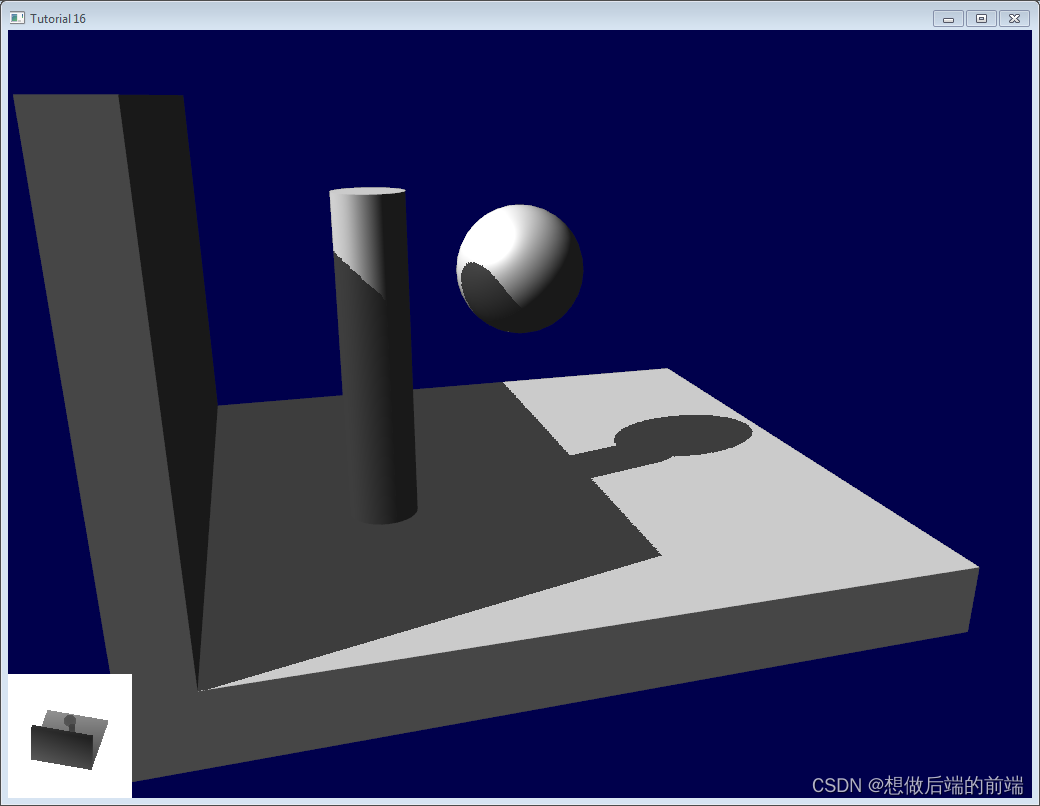
有一种有别于Bias的方法(但实际上也是殊途同归):
不使用Bias,第一个Pass(Light Camera记录深度的那个)设置成仅渲染背面(正面剔除)
这样可以让一些具有厚度的几何体背面作为深度记录,从而部分避免了几何体正面的 Shadow Acne现象。实际上这个跟使用了Bias+加厚几何体思想是差不多的,区别只不过在于:前者是低门限加一个偏移,后者则是直接给出高门限
1.5 Slope Scale Based Depth Bias
通过上面知道,Bias 过小时可能不能解决 Shadow Acne 现象,Bias 过大时又可能导致严重的 Peter Panning问题。
Slope Scale Based Depth Bias :为了尽可能减少由于 Bias 过大过小引起的问题,采取了根据平面倾角的一种自适应 Bias(例如:当光线与平面垂直时,Bias应该为0;当光线与平面的夹角越小,则Bias应越大)。
float bias = max(0.05 * (1.0 - dot(normal, lightDir)), 0.005);
二、Percentage Closer Filtering(PCF)
Shadow Mapping 还存在 阴影锯齿(Shadow Aliasing) 问题:

Percentage Closer Filtering(PCF)正是解决阴影锯齿的方案,它的核心想法是计算阴影时不是考虑单个采样点,而是在一定范围内进行多重采样,这样可以让阴影的边缘不那么锯齿,因为 Visibility 不再是非0即1,而是带有渐变的取值。
2.1 分布采样函数
在对周围一定范围内若干个坐标进行采样的时候,可以通过分布采样函数来确定 NUM_SAMPLES 个采样位置,为了让阴影边缘更加柔和,我们可以用一些较好的分布采样函数。
均匀圆盘分布采样(Uniform-Disk Sample):圆范围内随机取一系列坐标作为采样点;看上去比较杂乱无章,采样效果的 noise 比较严重。
泊松圆盘分布采样(Poisson-Disk Sample):圆范围内随机取一系列坐标作为采样点,但是这些坐标还需要满足一定约束,即坐标与坐标之间至少有一定距离间隔。

// 均匀圆盘分布
void uniformDiskSamples( const in vec2 randomSeed ) {
// 随机种子
float randNum = rand_2to1(randomSeed);
// 随机取一个角度
float sampleX = rand_1to1( randNum ) ;
float angle = sampleX * PI2;
// 随机取一个半径
float sampleY = rand_1to1( sampleX ) ;
float radius = sqrt(sampleY);
for( int i = 0; i < NUM_SAMPLES; i ++ ) {
disk[i] = vec2(radius * cos(angle) , radius * sin(angle));
// 继续随机取一个半径
sampleX = rand_1to1( sampleY ) ;
radius = sqrt(sampleY);
// 继续随机取一个角度
sampleY = rand_1to1( sampleX ) ;
angle = sampleX * PI2;
}
}
// 泊松圆盘分布
void poissonDiskSamples( const in vec2 randomSeed ) {
// 初始弧度
float angle = rand_2to1( randomSeed ) * PI2;
// 初始半径
float INV_NUM_SAMPLES = 1.0 / float( NUM_SAMPLES );
float radius = INV_NUM_SAMPLES;
// 一步的弧度
float ANGLE_STEP = 3.883222077450933;// (sqrt(5)-1)/2 *2PI
// 一步的半径
float radiusStep = radius;
for( int i = 0; i < NUM_SAMPLES; i ++ ) {
disk[i] = vec2(cos(angle),sin(angle)) * pow( radius, 0.75 );
radius += radiusStep;
angle += ANGLE_STEP;
}
}
2.2 PCF 算法过程
Percentage Closer Filtering(PCF) 的算法过程:
- 计算 Visibility 时,原本对 Shadow Map 的一次坐标采样换成对周围一定范围内若干个坐标进行采样。
- 各个采样结果同样用来与 z′ 做比较,最后取比较结果的平均作为 Visibility。
float visibility_PCF(sampler2D shadowMap, vec4 coords) {
const float bias = 0.005;
float sum = 0.0;
// 初始化泊松分布
poissonDiskSamples(coords.xy);
// 采样
for(int i = 0;i<NUM_SAMPLES;++i){
float depthInShadowmap = unpack(texture2D(shadowMap,coords.xy+disk[i]*0.001).rgba);
sum += ((depthInShadowmap + bias)< coords.z?0.0:1.0);
}
// 返还平均采样结果
return sum/float(NUM_SAMPLES);
}

2.3 硬件 PCF
所谓硬件 PCF 就是利用纹理采样器中的 compare func(如 DX11 中为 D3D11_COMPARISON_LESS_EQUAL)来实现深度大小比较计算,这样对 shadow map 采样的结果返还的不是阴影深度而是深度比较后的布尔结果(0或1),并且同时还需要启用 linear sampling 从而可以得到 2x2 texels filter 后的采样结果。
- 硬件 PCF 非常快速,只需一次采样操作即可完成,无需额外代码。
- 然而,硬件 PCF 只能计算 2x2 个 samples(相当于滤波核大小限制在了相邻的 2x2 shadow map texels
范围),只能让阴影边缘有一定程度的软化,并不能完全消除锯齿。
三、Percentage Closer Soft Shadows(PCSS)
Shadow Mapping 还存在硬阴影(Hard Shadow)的问题,因为现实世界的影子往往是软阴影(Soft Shadow)。
一个现实观察是,当投影物与阴影之间的距离越远,则阴影越软(如下图:笔尖阴影由于与笔尖的距离较近,因此阴影边缘较为锐利;而远处笔身阴影则因与笔身距离较远,阴影边缘较为发散且模糊)。

这是因为较大的光源面会有一些区域被遮蔽一部分光又接受一部分光,从而产生半影(Penumbra),直观看就是没那么暗的边缘处阴影。
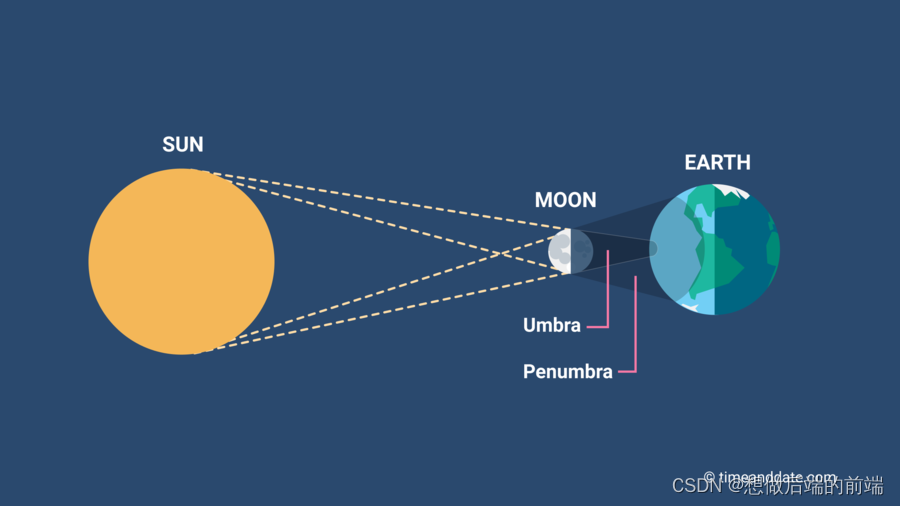
3.1 Penumbra Size
用二维平面的图去描述,实际上就是光源段W(light)两端与遮挡物连直线后打在被投影物上的即是 W(penumbra)也就是说这段半影需要有渐变的阴影效果。假如我们用 PCF 算法中的圆盘半径大小等同于这个半影段的尺寸W(penumbra)就能实现这段的渐变阴影效果(可以想想为什么)
现在,由下图的几何关系容易推出:

其中,W(Light)是光源面积尺寸, d(Blocker)是遮挡物的深度,d(receiver)是被投影物的深度(实际上就是 z‘)

但是 PCF 算法的圆盘半径大小是固定的,因此处处的边缘看起来都带有相同的渐变范围,这和我们看到的笔尖阴影现象不符合(近处边缘渐变应该更少些,远处边缘渐变应该多些),所以我们可以只要根据不同位置动态地修改圆盘半径大小(实际上就是动态地计算 W(penumbra)),这个也就是PCSS的核心部分。
3.2 Blocker Search
我们不能简单把一个投影点变换成Shadow Map的坐标后,直接拿单个坐标采样 ShadowMap 的深度来作为d(Blocker) 。这是因为投影点的单次采样实际上就是单一直线连向了光源面的中心,而这条直线要是没有碰到遮挡物(即 d(Blocker) == d(Receiver)),从而得出该投影点为全亮的结论。
但实际很多场景中(如下图),投影点和光源面处处连线后会发现有相当一部分光线会碰到遮挡物,因此该投影点应该属于半影范围内。
为此,我们可以对 ShadowMap 的一定范围内进行多重采样,每次采样得到的深度若小于d(Receiver) 则认为遇到遮挡物并算入平均遮挡深度的贡献,这样多重采样之后得到的平均遮挡深度就作为 d(Blocker)
如何确定采样的范围半径呢?两个参数决定:w(Light) 的尺寸、投影点与光源的距离(可以结合上图推理一下为什么)
 这样,计算 Blocker 平均遮挡深度的整个过程为:
这样,计算 Blocker 平均遮挡深度的整个过程为:
float findBlocker( sampler2D shadowMap, vec2 uv, float zReceiver ) {
float dBlocker = zReceiver * 0.01;
const float wLight = 0.006;
const float c = 100.0;
float wBlockerSearch = wLight * zReceiver * c;
float sum = 0.01; // 取0.01一是为了避免出现0除问题,二是当多重采样没有贡献时的dBlocker/sum将等于zReceiver
for(int i = 0;i<BLOCKER_SEARCH_NUM_SAMPLES;++i){
float depthInShadowmap = unpack(texture2D(shadowMap, uv + disk[i] * wBlockerSearch).rgba);
if(depthInShadowmap < zReceiver){
dBlocker += depthInShadowmap;
sum += 1.0;
}
}
return dBlocker/float(sum);
}
PCF算法效果图:

PCSS算法效果图:

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
