【c++&leetcode】1913.Maximum Product Difference Between Two Pairs
发布时间:2024年01月21日
这个问题很容易解决。只要将数组排序,返回 最大元素*第二大元素-最小元素*第二小元素 即可。通过这道题顺便复习一些排序算法?。
直接使用sort函数
class Solution {
public:
int maxProductDifference(vector<int>& nums) {
sort(nums.begin(), nums.end());
return *(nums.end()-1) * *(nums.end()-2) - *(nums.begin()) * *(nums.begin()+1);
}
};归并排序(merge sort): O(nlogn)
#include <string>
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
void mergeSort(std::vector<int>& array, int left, int right) {
if (left >= right)
return;
//middle = (left + right) / 2 -> integer overflow
int middle = left + (right - left) / 2; //avoid integer overflow
mergeSort(array, left, middle);
mergeSort(array, middle + 1, right);
int left_length = middle - left + 1;
int right_length = right - middle;
vector<int> leftArray(left_length);
vector<int> rightArray(right_length);
for (int i = 0; i < left_length; i++)
{
leftArray[i] = array[left + i];
}
for(int i = 0; i < right_length; i++)
{
rightArray[i] = array[middle+i+1];
}
int i = left, l = 0, r = 0;
while(l < left_length && r < right_length)
{
if (leftArray[l] <= rightArray[r])
{
array[i]=leftArray[l];
l++;
}
else{
array[i]=rightArray[r];
r++;
}
i++;
}
while (r < right_length)
{
array[i]=rightArray[r];
r++;
i++;
}
while (l < left_length)
{
array[i]=leftArray[l];
l++;
i++;
}
}
int maxProductDifference(vector<int>& nums) {
//merge sort
mergeSort(nums, 0, nums.size() - 1);
return *(nums.end()-1) * *(nums.end()-2) - *(nums.begin()) * *(nums.begin()+1);
}
};?关于归并排序算法的思想,请看这个视频。
时间复杂度分析如下:

题外话: merge sort递归结构像不像完全二叉树或者满二叉树:)
快速选择(quick sort): 超时
#include <string>
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
void quick_sort(vector<int>&nums, int start, int end){
if(start >= end)
return;
int pivot_value = nums[end];
int pIndex = 0;
for(int i = 0; i < end; i++)
{
if (nums[i] < pivot_value)
{
swap(nums[i], nums[pIndex]);
pIndex++;
}
}
swap(nums[pIndex], nums[end]);
quick_sort(nums, 0, pIndex - 1);
quick_sort(nums, pIndex + 1, end);
}
int maxProductDifference(vector<int>& nums) {
// quick sort
quick_sort(nums, 0, nums.size()-1);
return *(nums.end()-1) * *(nums.end()-2) - *(nums.begin()) * *(nums.begin()+1);
}
};不了解快速选择算法的朋友,强烈推荐这个视频。
超时的原因和时间复杂度有关。快速选择算法的最佳和平均时间复杂度为O(nlogn),最差的情况时间复杂度为O(n^2)。推导如下
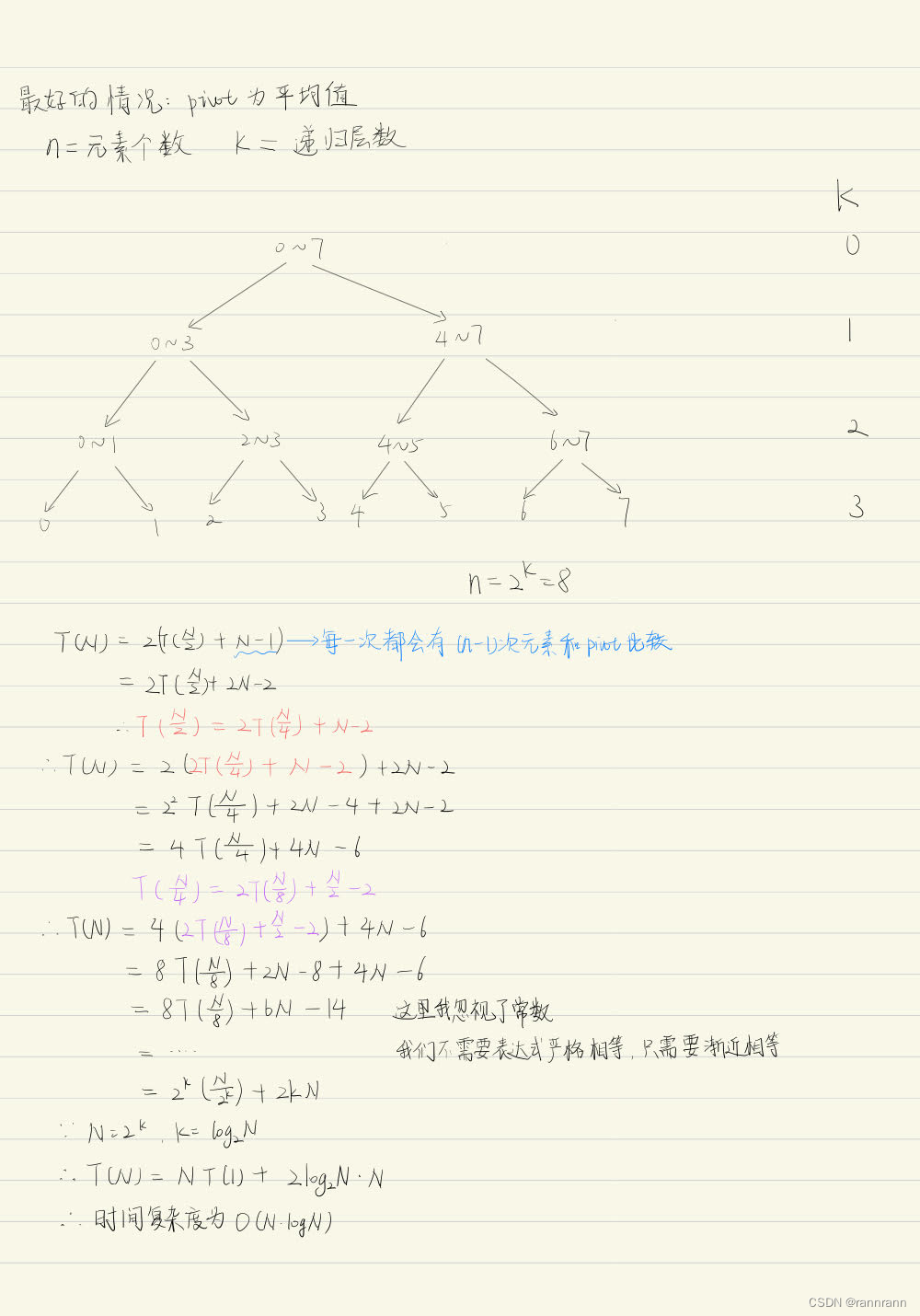
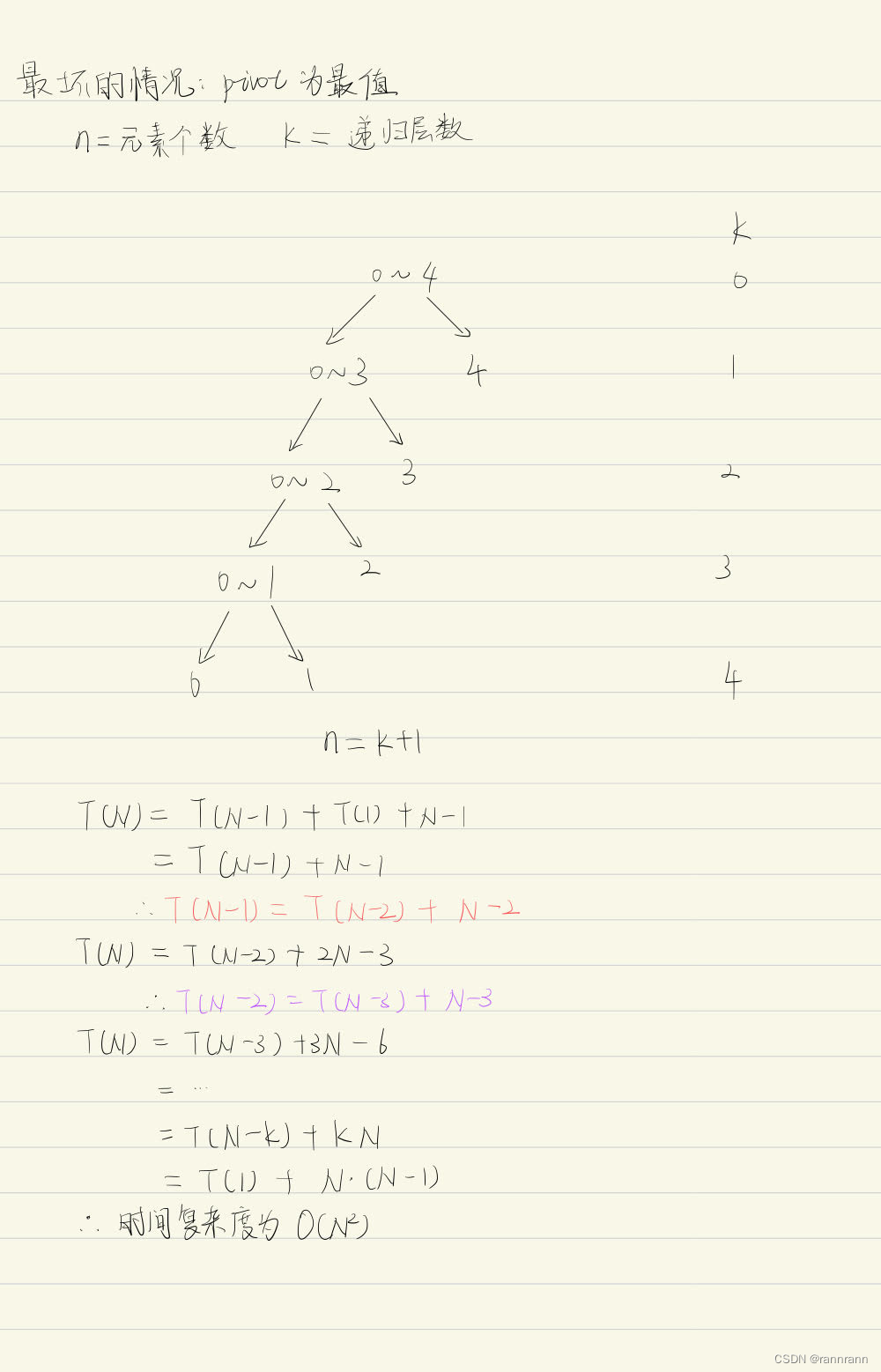
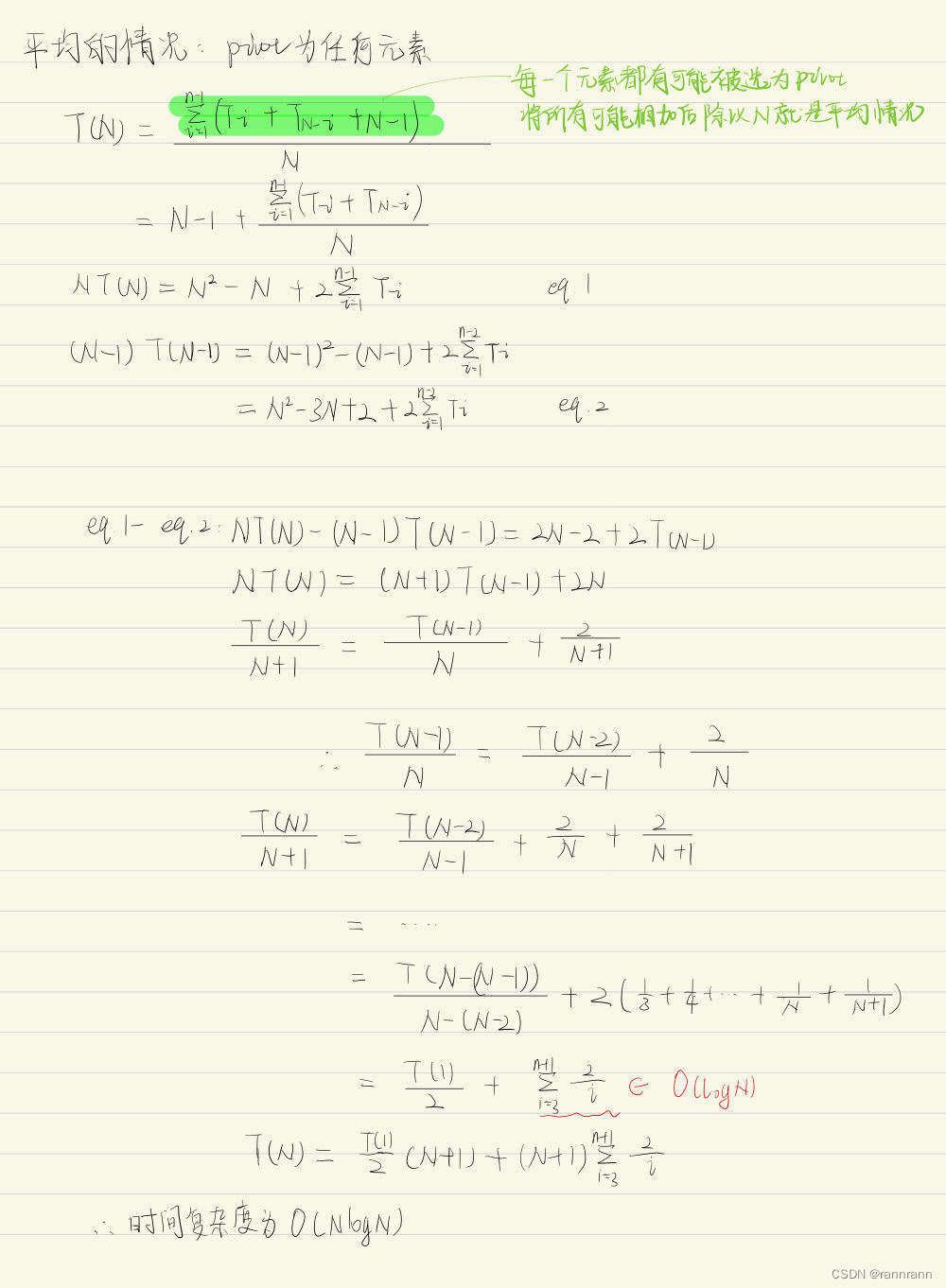
文章来源:https://blog.csdn.net/qq_37120435/article/details/135347338
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!