代码随想录算法训练营第四天 |24.两两交换链表中的节点，19.删除链表的倒数第N个节点，面试题02.07.链表相交，142、环形链表II

链表基础

1、链表定义：

（1）链表是一种通过指针串联在一起的线性结构，每一个节点由两部分组成，一个是数据域一个是指针域（存放指向下一个节点的指针），最后一个节点的指针域指向null（空指针的意思）。

（2）链表的入口节点称为链表的头结点也就是head。

2、链表类型：

单链表：上面说的就是单链表。

双链表：

单链表中的指针域只能指向节点的下一个节点。

双链表：每一个节点有两个指针域，一个指向下一个节点，一个指向上一个节点。

双链表 既可以向前查询也可以向后查询。

循环列表：

循环链表，顾名思义，就是链表首尾相连。

循环链表可以用来解决约瑟夫环问题。

3、数组是在内存中是连续分布的，但是链表在内存中可不是连续分布的。

链表是通过指针域的指针链接在内存中各个节点。

所以链表中的节点在内存中不是连续分布的 ，而是散乱分布在内存中的某地址上，分配机制取决于操作系统的内存管理。

203.两两交换链表中的节点

1、题目链接：代码随想录

2、文章讲解：代码随想录

3、视频讲解： 帮你把链表细节学清楚！ | LeetCode：24. 两两交换链表中的节点_哔哩哔哩_bilibili

4、题目：

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。

你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

添加虚拟节点解法

• 时间复杂度：O(n)
• 空间复杂度：O(1)

class Solution {
    // 虚拟头节点
    public ListNode swapPairs(ListNode head) {
        // 定义一个虚拟头节点
        ListNode dumy = new ListNode(-1, head);
        // 当前节点为虚拟头节点
        ListNode cur = dumy;
        ListNode temp;
        // 定义一个临时节点，用于保存两个节点的第一个节点
        ListNode firstNode;
        // 定义一个临时节点，用于保存两个节点的第二个节点
        ListNode secondNode;
        while (cur.next != null && cur.next.next != null) {
            // 临时节点，保存每次遍历的第三个节点
            temp = cur.next.next.next;
            // 每次遍历的第一个节点
            firstNode = cur.next;
            // 每次遍历的第二个节点
            secondNode = cur.next.next;
            // 步骤一，虚拟头节点到第二个节点的连接
            cur.next = secondNode;
            // 步骤二，第二个节点到第一个节点的连接
            secondNode.next = firstNode;
            // 步骤三，第一个节点到第三个节点的连接
            firstNode.next = temp;
            // 移动到下一轮交换
            cur = firstNode;
        }
        return dumy.next;
    }
}

递归解法

/**
 * 函数名为swapPairs，其输入参数是一个类型为ListNode的头节点，表示一个链表。
 * 首先进行基本情况判断：如果头节点为空（即链表为空）或者头节点的下一个节点为空（即链表只有一个节点），则无需进行交换操作，直接返回当前头节点即可。
 * 获取当前处理到的节点（即头节点）的下一个节点，并将其赋值给变量next。这里我们关注的是每一对相邻节点的交换，所以next将是即将被交换的第一个节点。
 * 进行递归调用：将next节点的下一个节点作为新的头节点，再次调用swapPairs函数，这样会逐对地处理整个链表后续的所有节点对。
 * 递归调用结束后，返回一个新的节点newNode，它是原next节点下一对节点交换后的结果。
 * 现在开始执行真正的节点交换操作：将next节点的next指针指向head节点，也就是让原链表中的第二个节点指向第一个节点，完成了一次节点交换。
 * 同时，将head节点的next指针指向newNode，这样就将已经完成交换的后续部分与当前这对节点正确地连接了起来。
 * 最后，返回next节点作为新的链表头节点。经过这样的递归过程，原始链表的所有相邻节点对都将得到交换，最终得到的链表即为所有节点两两交换后的结果。
 */
class Solution {
    // 递归解法
    public ListNode swapPairs(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        // 获取当前节点的下一个节点
        ListNode next = head.next;
        // 递归调用
        ListNode newNode = swapPairs(next.next);
        // 这里进行交换
        next.next = head;
        head.next = newNode;
        return next;

    }
}

19. 删除链表的倒数第N个节点

1、题目链接：代码随想录

2、文章讲解：代码随想录

3、视频讲解：链表遍历学清楚！ | LeetCode：19.删除链表倒数第N个节点_哔哩哔哩_bilibili

4、题目：

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

进阶：你能尝试使用一趟扫描实现吗？

5、注意点：双指针的经典应用，如果要删除倒数第n个节点，让fast移动n步，然后让fast和slow同时移动，直到fast指向链表末尾。删掉slow所指向的节点就可以了。

双指针解法

• 时间复杂度: 涉及 index 的相关操作为 O(index), 其余为 O(1)
• 空间复杂度: O(n)

class Solution {
    双指针解法
    public ListNode removeNthFromEnd(ListNode head, int n) {
        // 定义虚拟头节点
        ListNode dumy = new ListNode(0, head);
        // 定义快指针
        ListNode fastNode = dumy;
        // 定义慢指针
        ListNode slowNode = dumy;
        // 【重要】快指针先走 n+1 步,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点（方便做删除操作）
        for (int i = 0; i <= n; i++) {
            fastNode = fastNode.next;
        }
        // 快指针和慢指针一起走
        while (fastNode != null) {
            fastNode = fastNode.next;
            slowNode = slowNode.next;
        }
        // 删除倒数第 n 个结点
        slowNode.next = slowNode.next.next;
        return dumy.next;
    }
}

19、面试题02.07.链表相交

1、题目链接：代码随想录

2、文章讲解：代码随想录

3、题目：

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

4、思路：

简单来说，就是求两个链表交点节点的指针。 这里同学们要注意，交点不是数值相等，而是指针相等。

5、注意点：

保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

• 时间复杂度：O(n + m)
• 空间复杂度：O(1)

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode curA = headA;
        ListNode curB = headB;
        int lenA = 0;
        int lenB = 0;
        // 计算两个链表的长度
        while (headA != null) {
            lenA++;
            headA = headA.next;
        }
        while (headB != null) {
            lenB++;
            headB = headB.next;
        }
        curA = headA;
        curB = headB;
        // 让curA先走长的
        if (lenB > lenA) {
            // 交换lenA和lenB
            int temp = lenA;
            lenA = lenB;
            lenB = temp;
            // 交换curA和curB
            ListNode temp2 = curA;
            curA = curB;
            curB = temp2;
        }
        // 求出差值
        int diff = lenA - lenB;
        // curA先走diff步
        for (int i = 0; i < diff; i++) {
            curA = curA.next;
        }
        // curA和curB同时走，遇到相同节点则返回
        while (curA != null) {
            if (curA == curB) {
                return curA;
            }
            curA = curA.next;
            curB = curB.next;
        }
        return null;
    }
}

142、环形链表II

1、题目链接：代码随想录

2、文章讲解：代码随想录

3、视频讲解：

把环形链表讲清楚！ 如何判断环形链表？如何找到环形链表的入口？ LeetCode：142.环形链表II_哔哩哔哩_bilibili

4、题目：

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

5、难点：

• 判断链表是否环
• 如果有环，如何找到这个环的入口

6、思路：

判断链表是否有环

可以使用快慢指针法，分别定义 fast 和 slow 指针，从头结点出发，fast指针每次移动两个节点，slow指针每次移动一个节点，如果 fast 和 slow指针在途中相遇 ，说明这个链表有环。

因为fast是走两步，slow是走一步，其实相对于slow来说，fast是一个节点一个节点的靠近slow的，所以fast一定可以和slow重合。

如果有环，如何找到这个环的入口

假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。 如图所示：

那么相遇时： slow指针走过的节点数为: x + y， fast指针走过的节点数：x + y + n (y + z)，n为fast指针在环内走了n圈才遇到slow指针， （y+z）为 一圈内节点的个数A。

因为fast指针是一步走两个节点，slow指针一步走一个节点， 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2：

(x + y) * 2 = x + y + n (y + z)

两边消掉一个（x+y）: x + y = n (y + z)

因为要找环形的入口，那么要求的是x，因为x表示 头结点到 环形入口节点的的距离。

所以要求x ，将x单独放在左面：x = n (y + z) - y ,

再从n(y+z)中提出一个 （y+z）来，整理公式之后为如下公式：x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的，因为 fast指针至少要多走一圈才能相遇slow指针。

这个公式说明什么呢？

先拿n为1的情况来举例，意味着fast指针在环形里转了一圈之后，就遇到了 slow指针了。

当 n为1的时候，公式就化解为 x = z，

这就意味着，从头结点出发一个指针，从相遇节点 也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候就是 环形入口的节点。

也就是在相遇节点处，定义一个指针index1，在头结点处定一个指针index2。

让index1和index2同时移动，每次移动一个节点， 那么他们相遇的地方就是 环形入口的节点。

动画如下：

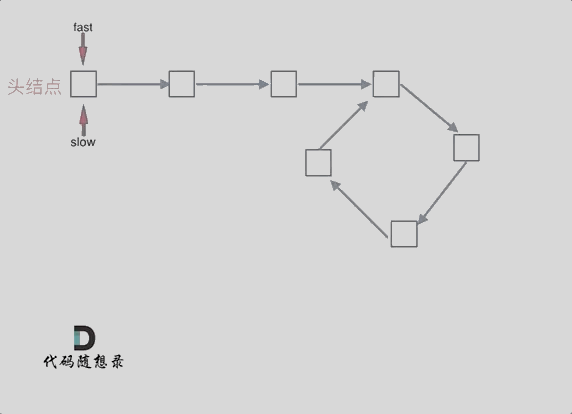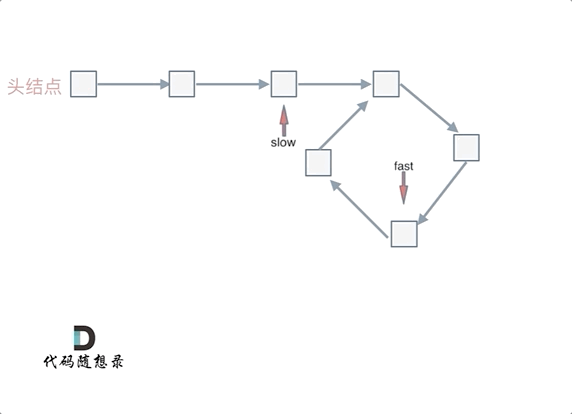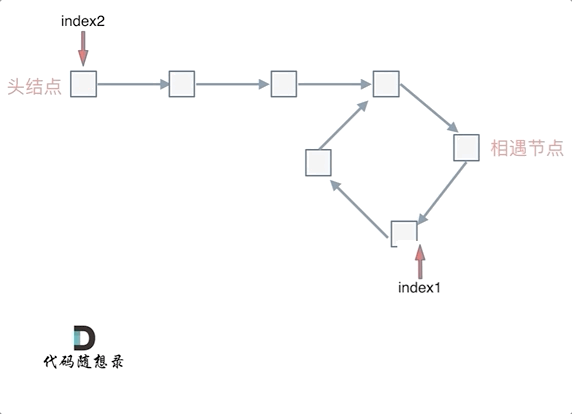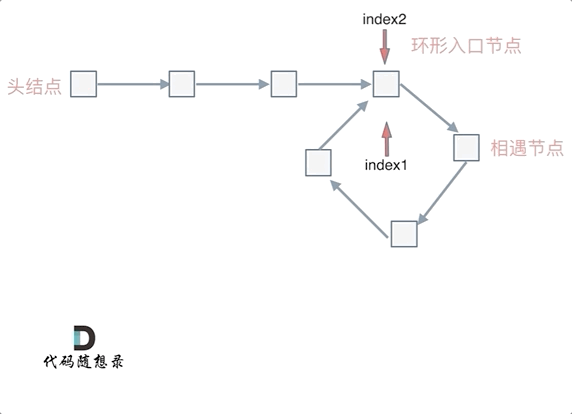
那么 n如果大于1是什么情况呢，就是fast指针在环形转n圈之后才遇到 slow指针。

其实这种情况和n为1的时候 效果是一样的，一样可以通过这个方法找到 环形的入口节点，只不过，index1 指针在环里 多转了(n-1)圈，然后再遇到index2，相遇点依然是环形的入口节点。

• 时间复杂度: O(n)，快慢指针相遇前，指针走的次数小于链表长度，快慢指针相遇后，两个index指针走的次数也小于链表长度，总体为走的次数小于 2n
• 空间复杂度: O(1)

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while (fast != null && fast.next != null) {
            // 快指针每次走两步，慢指针每次走一步
            slow = slow.next;
            fast = fast.next.next;
            // 判断是否有环
            if (slow == fast) {
                ListNode index1 = fast;
                ListNode index2 = head;
                // 【重点】两个指针，从头节点和相遇点开始，各走一步，直到相遇，此时相遇点就是环的入口
                while (index1 != index2) {
                    index1 = index1.next;
                    index2 = index2.next;
                }
                return index1;
            }
        }
        return null;
    }
}