机器学习---Adaboost算法
1.?Adaboost算法介绍
Adaboost是一种迭代算法,其核心思想是针对同一个训练集训练不同的分类器(弱分类器),然
后把这些弱分类器集合起来,构成一个更强的最终分类器(强分类器)。Adaboost算法本身是通
过改变数据分布来实现的,它根据每次训练集之中每个样本的分类是否正确,以及上次的总体分类
的准确率,来确定每个样本的权值。将修改过权值的新数据集送给下层分类器进行训练,最后将每
次得到的分类器最后融合起来,作为最后的决策分类器。
目前,对Adaboost算法的研究以及应用大多集中于分类问题,同时近年也出现了一些在回归问题
上的应用。就其应用adaboost系列主要解决了:两类问题、多类单标签问题、多类多标签问题、大
类单标签问题,回归问题。它用全部的训练样本进行学习。使用adaboost分类器可以排除一些不必
要的训练数据特征,并将关键放在关键的训练数据上面。
该算法其实是一个简单的弱分类算法提升过程,这个过程通过不断的训练,可以提高对数据的分类
能力。
①先通过对N个训练样本的学习得到第一个弱分类器;
②将分错的样本和其他的新数据一起构成一个新的N个的训练样本,通过对这个样本的学习得到第
二个弱分类器;
③将1和2都分错了的样本加上其他的新样本构成另一个新的N个的训练样本,通过对这个样本的学
习得到第三个弱分类器
④最终经过提升的强分类器。即某个数据被分为哪一类要通过......的多数表决。
对于boosting算法,存在两个问题:
①如何调整训练集,使得在训练集上训练的弱分类器得以进行;
②如何将训练得到的各个弱分类器联合起来形成强分类器。
针对以上两个问题,AdaBoost算法进行了调整:
①使用加权后选取的训练数据代替随机选取的训练样本,这样将训练的焦点集中在比较难分的训练
数据样本上;
②将弱分类器联合起来,使用加权的投票机制代替平均投票机制。让分类效果好的弱分类器具有较
大的权重,而分类效果差的分类器具有较小的权重。?
与Boosting算法不同的是,AdaBoost算法不需要预先知道弱学习算法学习正确率的下限即弱分类
器的误差,并且最后得到的强分类器的分类精度依赖于所有弱分类器的分类精度,这样可以深入挖
掘弱分类器算法的能力。?
AdaBoost算法中不同的训练集是通过调整每个样本对应的权重来实现的。开始时,每个样本对应
的权重是相同的,即其中n为样本个数,在此样本分布下训练出一弱分类器。对于分类错误的样
本,加大其对应的权重;而对于分类正确的样本,降低其权重,这样分错的样本就被突显出来,从
而得到一个新的样本分布。在新的样本分布下,再次对样本进行训练,得到弱分类器。依次类推,
经过T次循环,得到T个弱分类器,把这T个弱分类器按一定的权重叠加(boost)起来,得到最终
想要的强分类器。 ?
AdaBoost算法的具体步骤如下:
①给定训练样本集S,其中X和Y分别对应于正例样本和负例样本;T为训练的最大循环次数;
②初始化样本权重为1/n ,即为训练样本的初始概率分布;
③第一次迭代:(1)训练样本的概率分布相当,训练弱分类器;(2)计算弱分类器的错误率;(3)选取合
适阈值,使得误差最小;(4)更新样本权重;经T次循环后,得到T个弱分类器,按更新的权重叠
加,最终得到的强分类器。 ??
Adaboost算法是经过调整的Boosting算法,其能够对弱学习得到的弱分类器的错误进行适应性
(Adaptive)调整。上述算法中迭代了T次的主循环,每一次循环根据当前的权重分布对样本x定一个
分布P,然后对这个分布下的样本使用弱学习算法得到一个弱分类器,对于这个算法定义的弱学习
算法,对所有的样本都有错误率,而这个错误率的上限并不需要事先知道,实际上。每一次迭代,
都要对权重进行更新。更新的规则是:减小弱分类器分类效果较好的数据的概率,增大弱分类器分
类效果较差的数据的概率。最终的分类器是个弱分类器的加权平均。?
2. Adaboosting训练过程??
基于AdaBoost算法的强分类器训练
输入:(1)训练样本集![]()
其中,y =-1,训练样本xi为负样本,y =+1,训练样本xi为正样本
(2)弱分类器的学习算法L
(3)弱分类器的数目M
输出:一个由M个弱分类器构成的强分类器
训练过程:
①初始化训练样本xi权重![]() 若正负样本数目一致,则
若正负样本数目一致,则![]()
若正负样本数目分别为N+,N-,则
②for m=1,...,M
训练弱分类器![]() 估计弱分类器fm(x)的分类错误率em,如:
估计弱分类器fm(x)的分类错误率em,如:
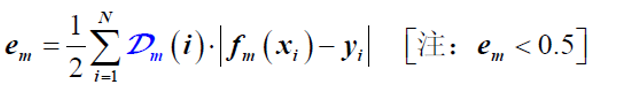
(3)估计弱分类器fm(x)的权重![]()
(4)基于弱分类器fm(x)调整各样本权重,并归一化调整:
归一化: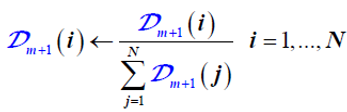 ,强分类器
,强分类器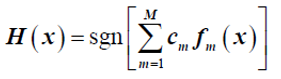 。
。
算法实现:

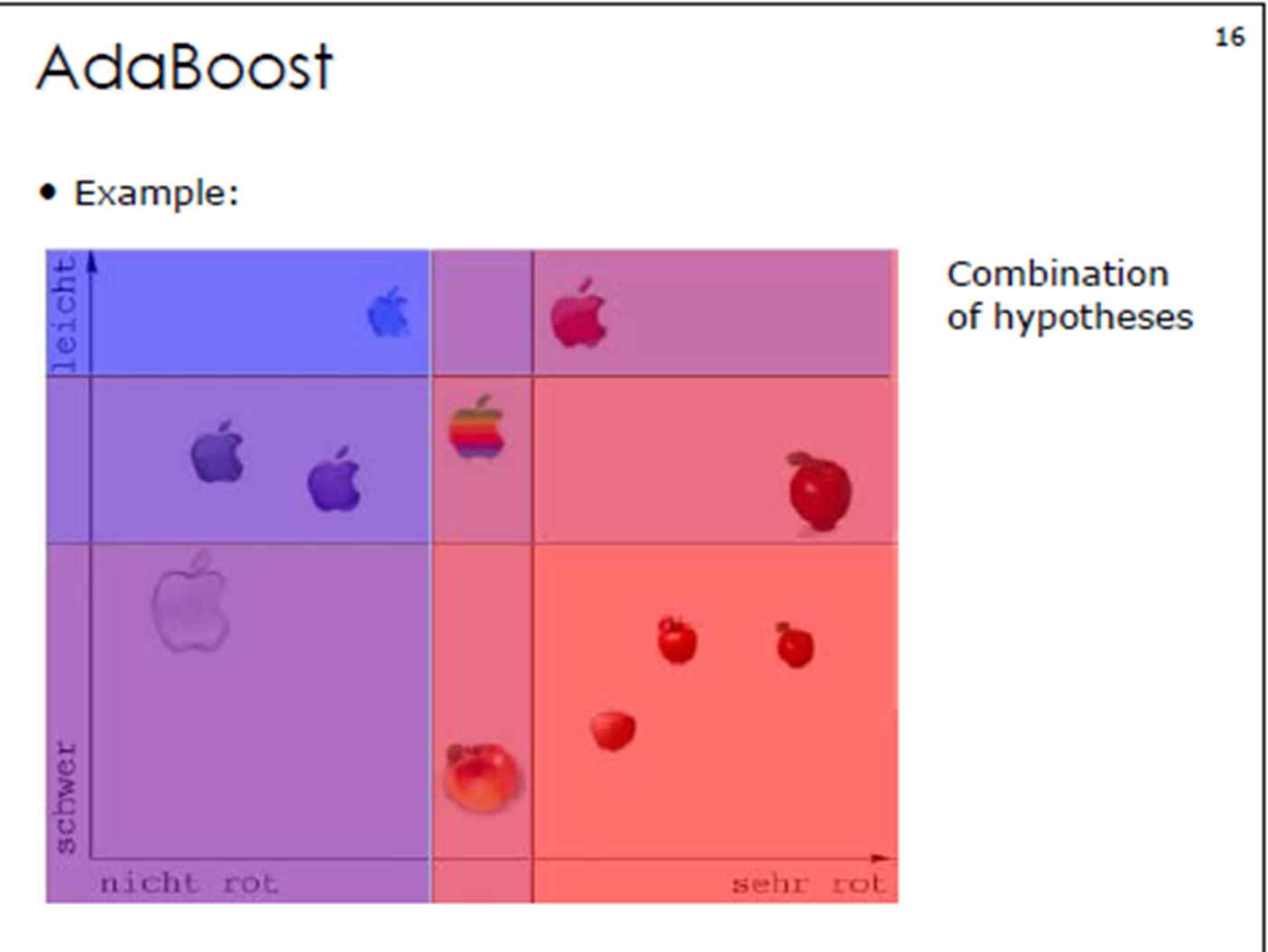
3.?Adaboost算法例子
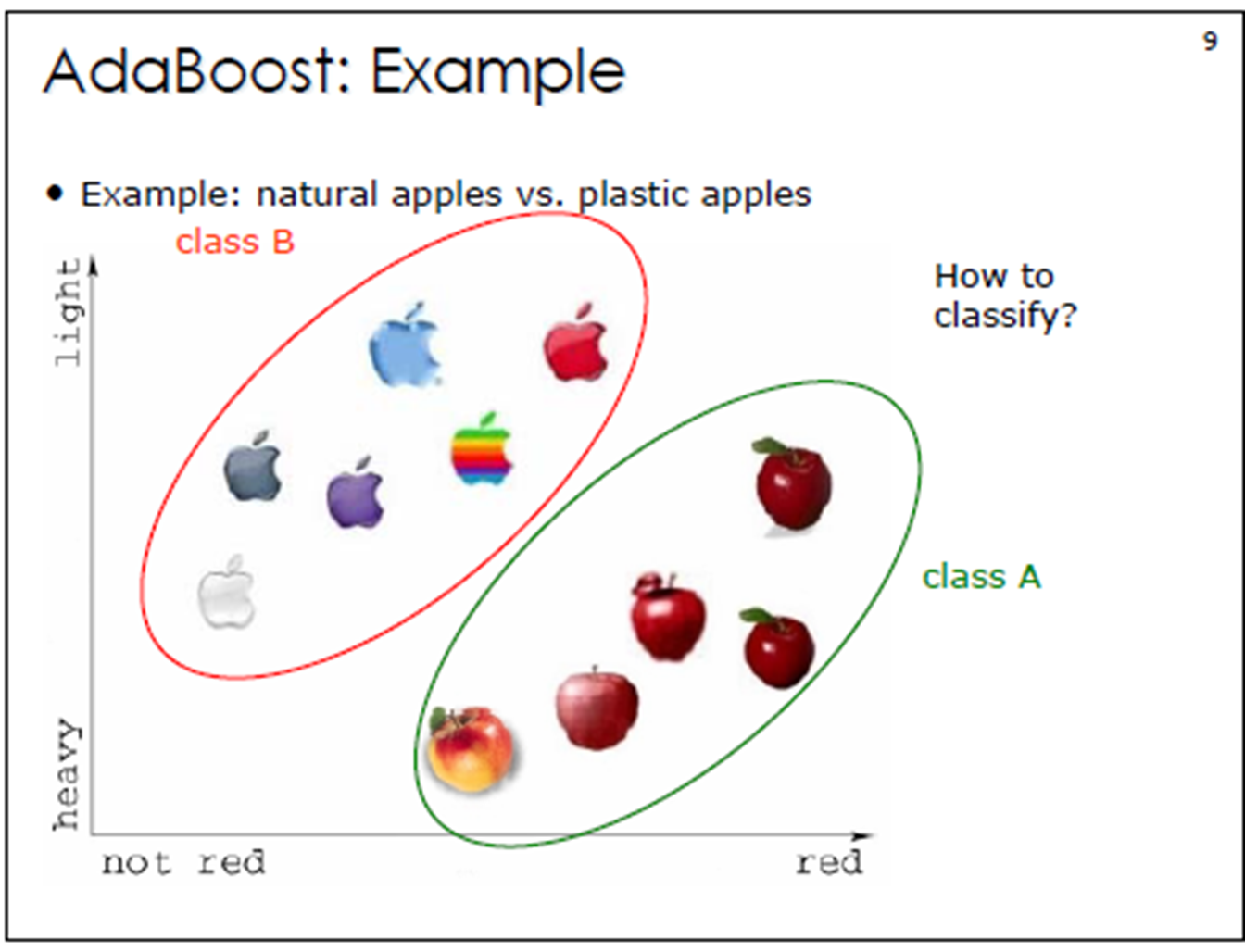 ?
?
 ?
?
 ?
?
 ?
?
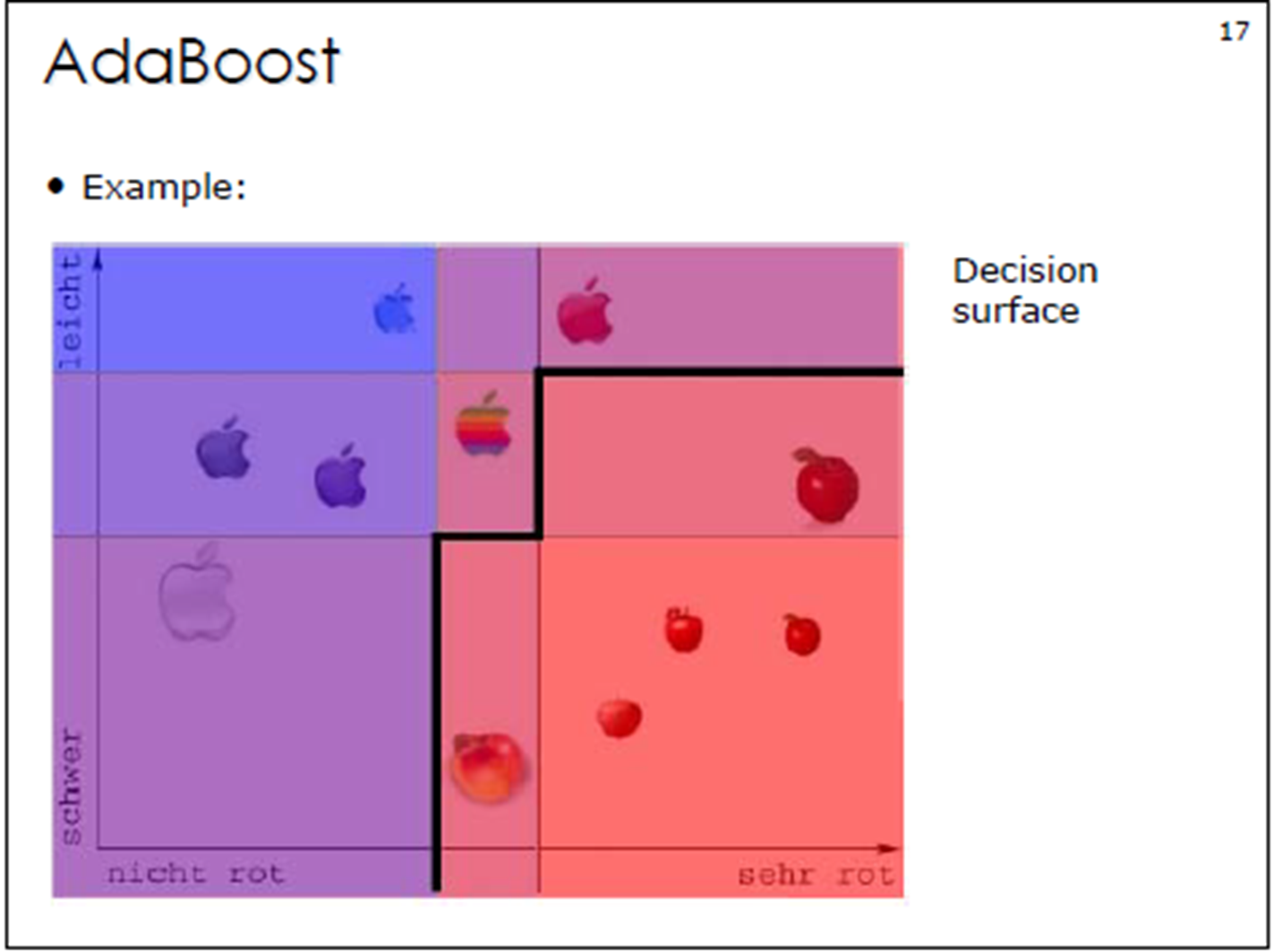 ?
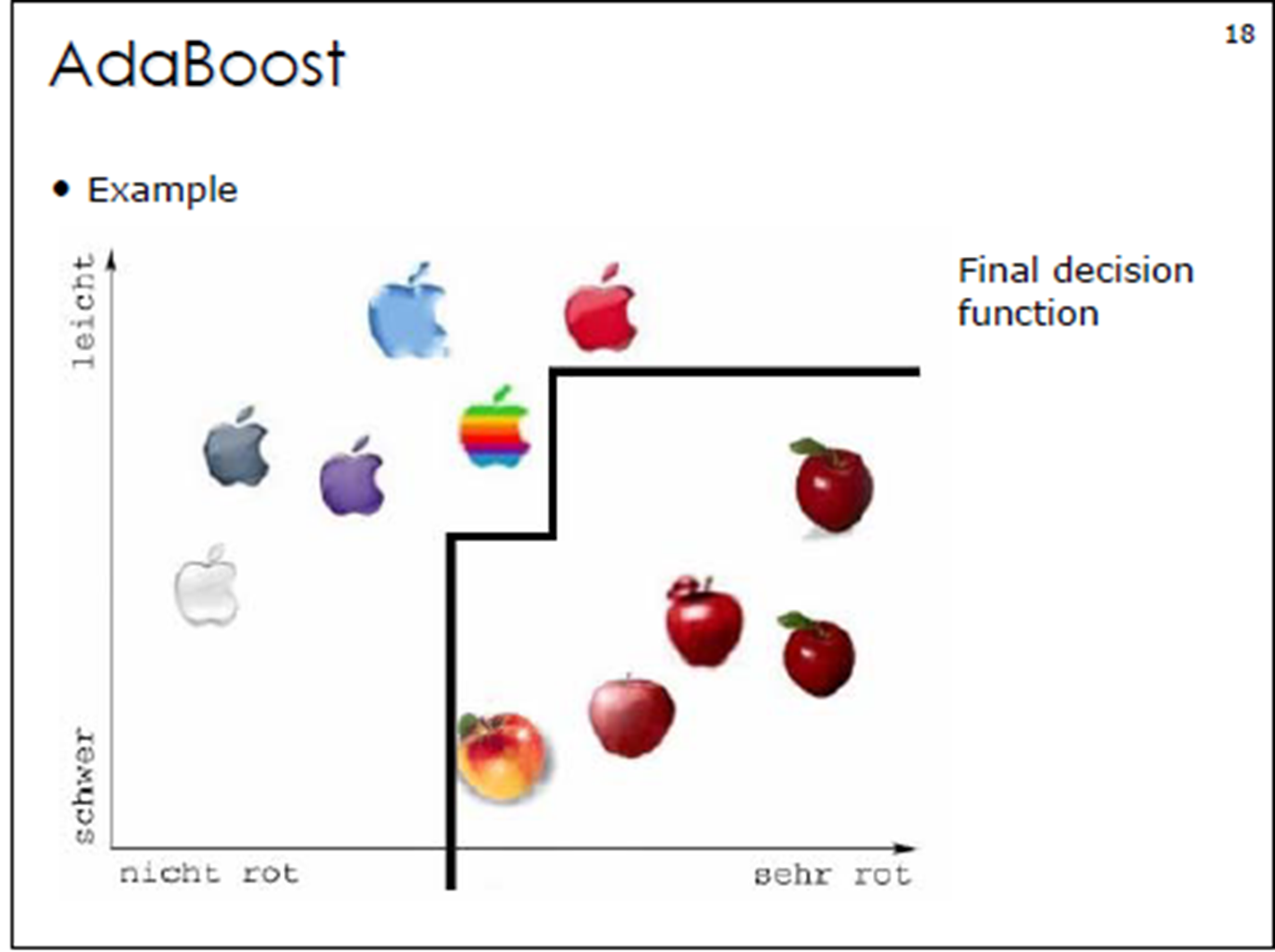
?
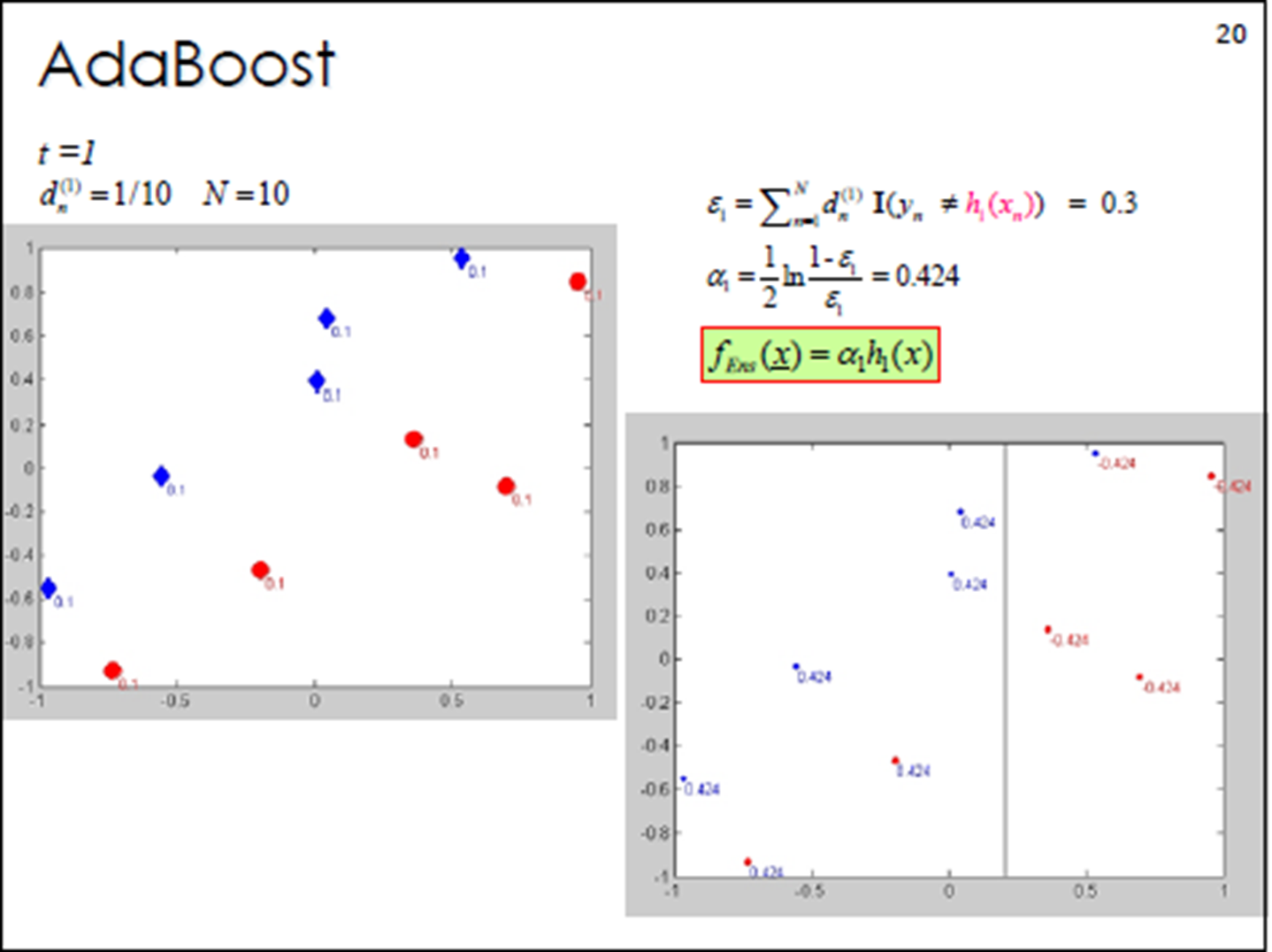 ?
?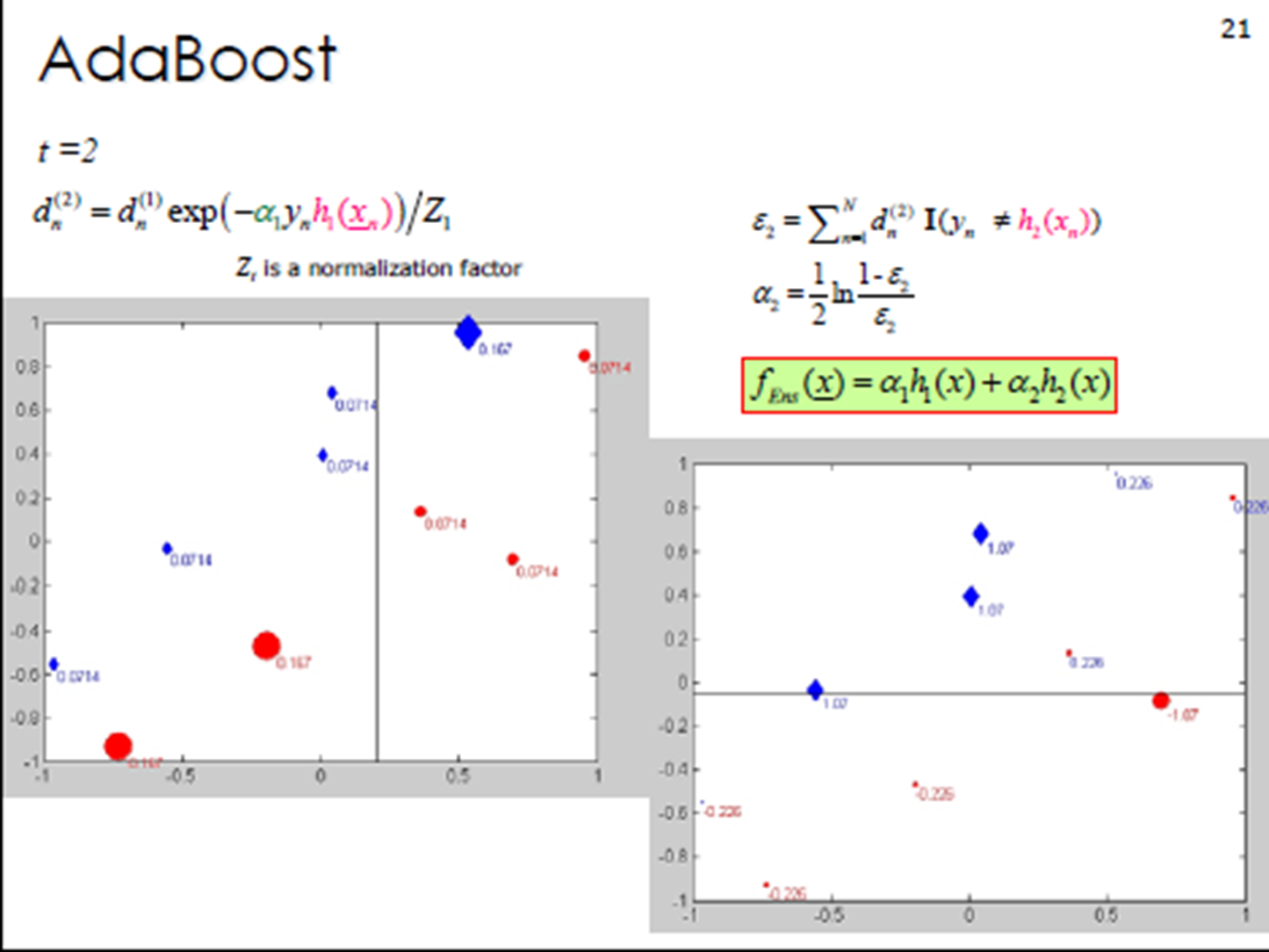
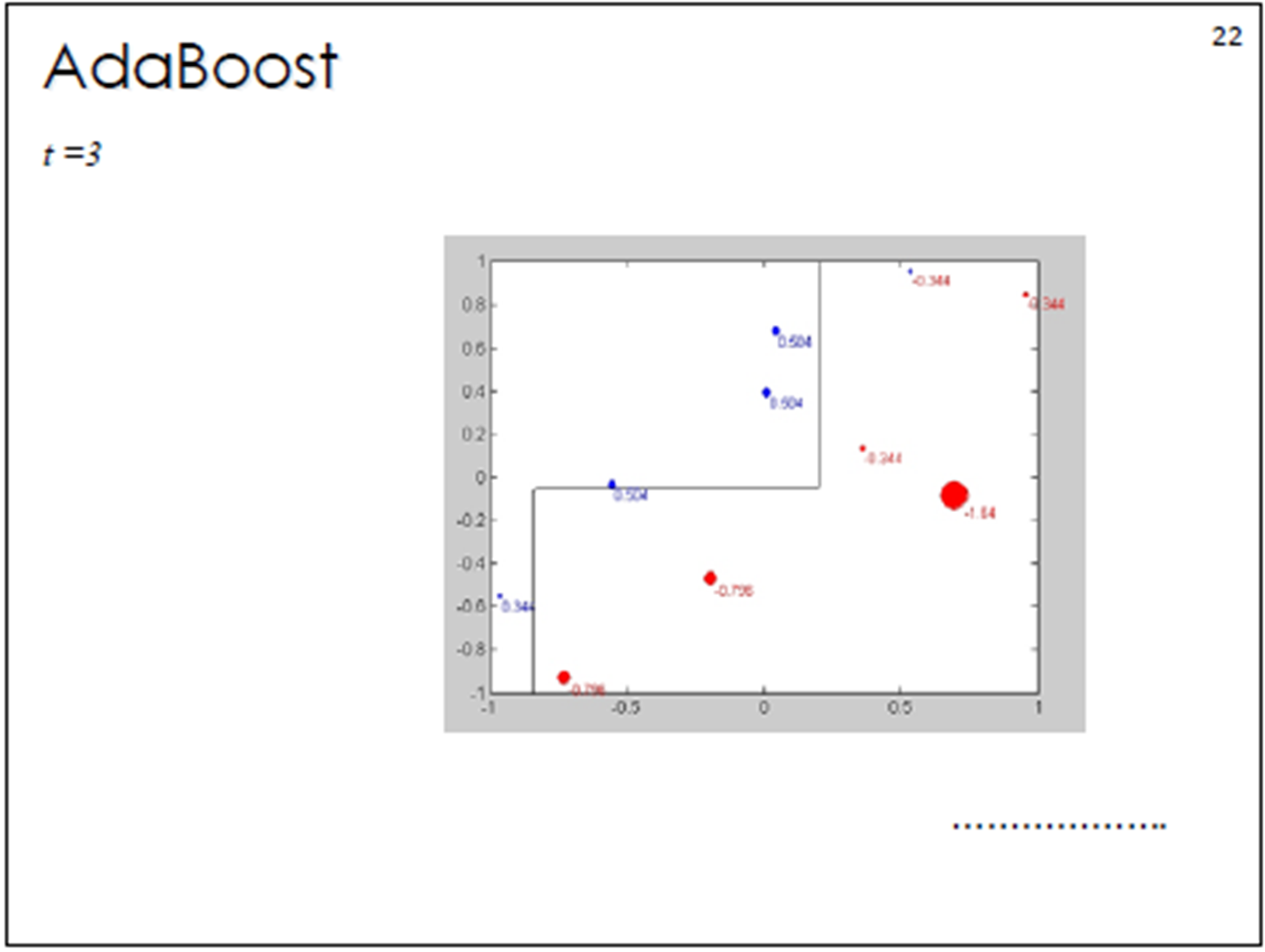 ?
?
3.?Adaboost算法计算案例
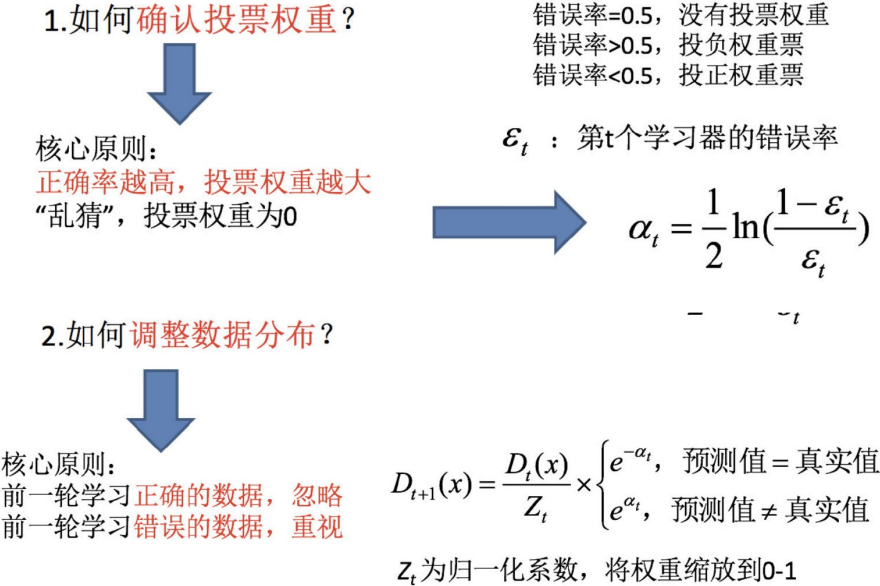
①初始化训练数据权重相等,训练第?个学习器。该假设每个训练样本在基分类器的学习中作用相
同,这?假设可以保证第?步能够在原始数据上学习基本分类器H1 (x)。
②AdaBoost反复学习基本分类器,在每?轮m = 1, 2, ..., M顺次的执?下列操作:
在权值分布为D的训练数据上,确定基分类器;
计算该学习器在训练数据中的错误率:![]()
计算该学习器的投票权重:![]()
根据投票权重,对训练数据重新赋权: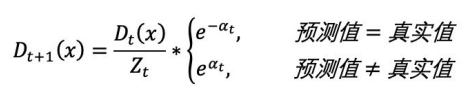
将下?轮学习器的注意?集中在错误数据上,重复执?上述计算步骤m次;
③对m个学习器进?加权投票: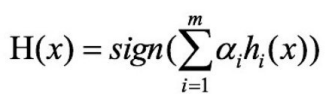
给定下?这张训练数据表所示的数据,假设弱分类器由xv产生,其阈值v使该分类器在训练数据集
上的分类误差率最低,试用Adaboost算法学习?个强分类器:

问题解答:
①初始化训练数据权重相等,训练第?个学习器:
![]()
![]()
②AdaBoost反复学习基本分类器,在每?轮m = 1, 2, ..., M顺次的执?下列操作:
当m=1的时候:在权值分布为D的训练数据上,阈值v取2.5时分类误差率最低,故基本分类器为:
![]() (6,7,8被分错)
(6,7,8被分错)
计算该学习器在训练数据中的错误率:![]()
计算该学习器的投票权重:![]()
根据投票权重,对训练数据重新赋权:![]()
根据下公式,计算各个权重值: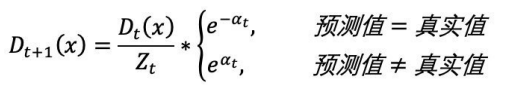
经计算得,D2的值为:![]()
计算过程: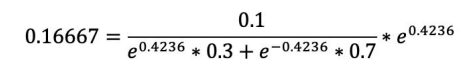
![]()
分类器H1(x)在训练数据集上有3个误分类点。
当m=2的时候:
在权值分布为D 的训练数据上,阈值v取8.5时分类误差率最低,故基本分类器为:
 (3,4,5被分错)
(3,4,5被分错)
计算该学习器在训练数据中的错误率:![]()
计算该学习器的投票权重:![]()
根据投票权重,对训练数据重新赋权:经计算得,D 的值为:

分类器H2(x)在训练数据集上有3个误分类点。
当m=3的时候:
在权值分布为D 的训练数据上,阈值v取5.5时分类误差率最低,故基本分类器为:
![]()
计算该学习器在训练数据中的错误率:![]()
计算该学习器的投票权重:![]()
根据投票权重,对训练数据重新赋权:经计算得,D4的值为:

分类器H3(x)在训练数据集上的误分类点个数为0。
③对m个学习器进行加权投票,获取最终分类器:
![]()
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 网址前有“安全锁”,网站就一定安全吗?
- 目标检测数据集 - 戴口罩检测数据集下载「包含VOC、COCO、YOLO三种格式」
- 关于对象存储的若干事
- exp imp 详解 include 不通用 content DATA_ONLY
- 集团数字化管理系统有哪些
- Pointnet++改进注意力机制系列:全网首发CPCA通道先验卷积注意力机制 |即插即用,实现有效涨点
- Ubuntu 从零开始配置环境
- php的file_put_contents()是不安全的?
- 深度学习(3)--递归神经网络(RNN)和词向量模型Word2Vec
- 克魔助手:方便查看iPhone应用实时日志和奔溃日志工具