【代码随想录】刷题笔记Day52

前言

• 周一到周三学车+考科二科三去了，科二挂了呜呜呜，等放假回来再考，收收心全力刷题

1143. 最长公共子序列 - 力扣（LeetCode）

• 求的是不连续的公共子序列，类似上一篇中的【最长重复子数组】，比较两个数组要用二维dp数组，定义[0, i-1]和[0, j-1]方便初始化
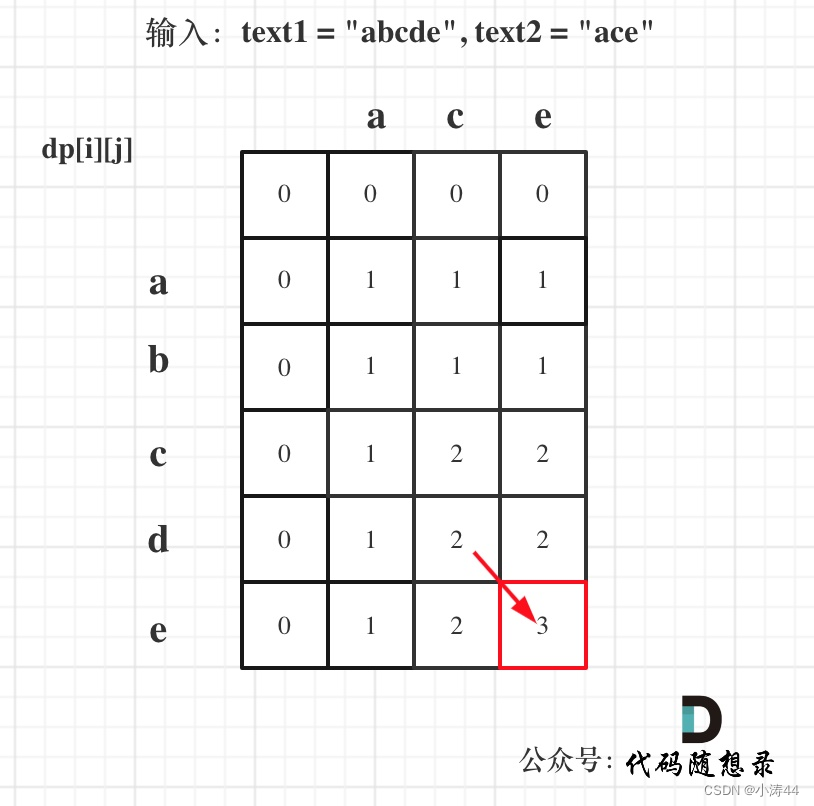
• dp[i][j]含义
  • 长度为[0, i - 1]的text1与长度为[0, j - 1]的ext2的最长公共子序列为dp[i][j]
• 递推公式
  • text1[i - 1] 与 text2[j - 1]相同：dp[i][j] = dp[i - 1][j - 1] + 1;
  • text1[i - 1] 与 text2[j - 1]不相同：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
• 初始化
  • 统一初始为0，顺序从上到下，从左到右
• 

• class Solution {
  public:
      int longestCommonSubsequence(string text1, string text2) {
          int len1 = text1.size();
          int len2 = text2.size();
          vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));
          for(int i = 1; i <= len1; i++){
              for(int j = 1; j <= len2; j++){
                  if(text1[i - 1] == text2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                  else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
              }
          }
          return dp[len1][len2];
      }
  };

1035. 不相交的线 - 力扣（LeetCode）

• 连线问题其实就是【最长公共子序列】问题，和上题一模一样

• class Solution {
  public:
      int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
          int len1 = nums1.size();
          int len2 = nums2.size();
          vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));
          for(int i = 1; i <= len1; i++){
              for(int j = 1; j <= len2; j++){
                  if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                  else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
              }
          }
          return dp[len1][len2];
      }
  };

?53. 最大子数组和 - 力扣（LeetCode）

• 贪心法在之前【代码随想录】刷题笔记Day34-CSDN博客写过，这里用动规法
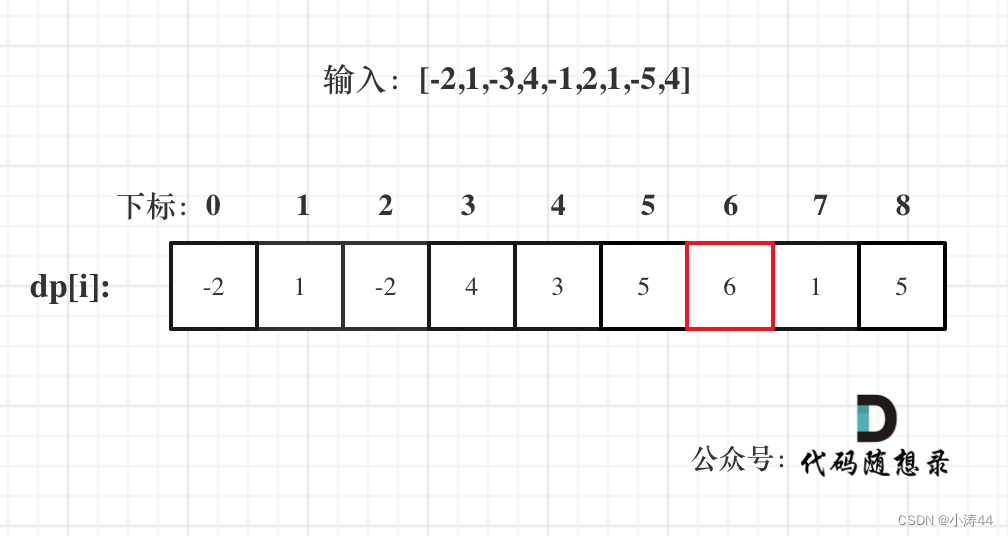
• dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]
• dp[i] = max(dp[i - 1] + nums[i], nums[i]);
• dp[0] = nums[0]，从前往后遍历，结果取最大
• 

• class Solution {
  public:
      int maxSubArray(vector<int>& nums) {
          if (nums.size() == 0) return 0;
          vector<int> dp(nums.size());
          dp[0] = nums[0];
          int result = dp[0];
          for (int i = 1; i < nums.size(); i++) {
              dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式
              if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值
          }
          return result;
      }
  };

?392. 判断子序列 - 力扣（LeetCode）

• ?双指针法

  • 思路很简单：相等一起跳，不等只跳j，最后判断是不是都跳完

  • class Solution {
    public:
        bool isSubsequence(string s, string t) {
            int i = 0, j = 0;
            while(i < s.size() && j < t.size()){
                if(s[i] == t[j]){  // 相等则一起跳ij
                    i++;
                    j++;
                }else{
                    j++;  // 不相等则只跳j
                }
            }
            if(j == t.size() && i < s.size()) return false;  // s没遍历完
            else return true;  // 都遍历完了
        }
    };

• ?动规法

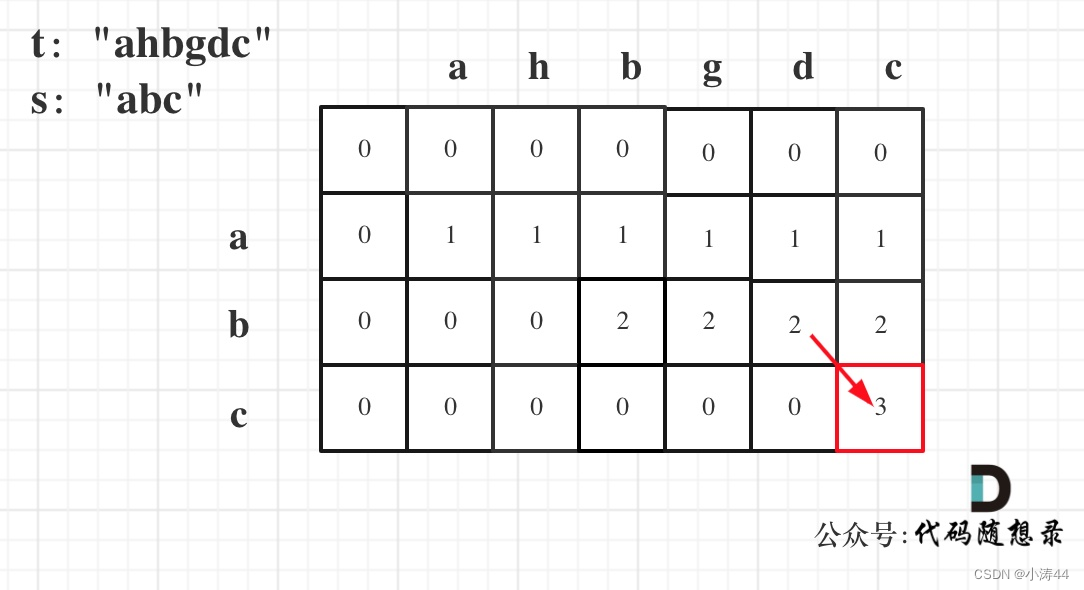
  • 类似【最长公共子序列】，最后判断长度与s相等即可，也是编辑距离入门题
  • 可修改：if(s[i - 1] != t[j - 1])? dp[i][j] = dp[i][j - 1]; （删除字符串t的元素）
  • 

  • class Solution {
    public:
        bool isSubsequence(string s, string t) {
            int len1 = s.size();
            int len2 = t.size();
            vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));
            for(int i = 1; i <= len1; i++){
                for(int j = 1; j <= len2; j++){
                    if(s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                    else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                    // 删除元素 else dp[i][j] = dp[i][j - 1];
                }
            }
            if(dp[len1][len2] == len1) return true;
            else return false;
        }
    };

?后言

• 刷累了......今天如果不开组会将是多么美好的一天！我就可以打球+继续刷题啦