【分治算法2.1】递归算法案例(C++实现)
发布时间:2023年12月18日
1.什么是递归算法
直接或间接地调用自身的算法称为递归算法。
2.案例
2.1?阶乘函数
阶乘函数可递归地定义为:

C++代码:
#include <iostream>
using namespace std;
int factorial(int n) {
if (n == 0)
return 1;
return n * factorial(n - 1);
}
int main()
{
int n;
cout << "求n的阶乘,请输入n值: ";
cin >> n;
cout << n <<"的阶乘是:" << factorial(n);
}2.2 Fibonacci数列
无穷数列1,1,2,3,5,8,13,21,34,55,……,称为Fibonacci数列。
它可以递归地定义为:

C++代码:
#include <iostream>
using namespace std;
int fibonacci(int n) {
if (n <= 1)
return 1;
return fibonacci(n - 1) + fibonacci(n - 2);
}
int main()
{
int n;
cout << "请输入Fibonacci数列的位置n: ";
cin >> n;
cout << "Fibonacci数列的第"<<n << "个位置的值是:" << fibonacci(n);
}?2.3?Ackerman函数
当一个函数及它的一个变量是由函数自身定义时,称这个函数是双递归函数。
Ackerman函数A(n,m)定义如下:

C++代码:
#include <iostream>
using namespace std;
int ackermann(int n, int m)
{
if (n == 1 && m == 0)
return 2;
else if (n == 0 && m >= 0)
return 1;
else if (n >= 2 && m == 0)
return n + 2;
else // else if (m >= 1 && n >= 1)
return ackermann(ackermann(n - 1, m), m - 1);
}
int main()
{
int n ;
int m ;
cout << "输入n的值:";
cin >>n;
cout << "输入m的值:";
cin >> m;
cout << "ackermann(" << n << "," << m << ")的值为:" << ackermann(n, m);
}2.4Hanoi塔问题
设a,b,c是3个塔座。要求圆盘由a移动到b。移动圆盘时遵守以下移动规则:
规则1:每次只能移动1个圆盘;
规则2:任何时刻都不允许较大的圆盘压在较小的圆盘之上;
规则3:在满足移动规则1和2的前提下,可将圆盘移至a,b,c中任一塔座上。
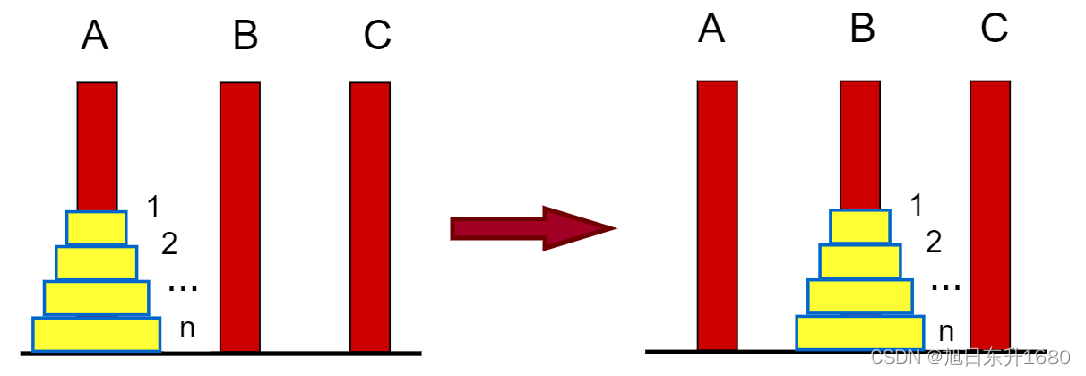
?方法:
第一步:将(n-1)个盘子从A搬到C(借助B)
第二步:将A塔座中,最低端的大盘子n从A搬到B
第三步:将C上的(n-1)盘子,借助A移动到B

C++代码:
#include<iostream>
using namespace std;
//void Hannoi(int, char, char, char);
int sum = 0;
void Move(int i, char M, char N)
{ //打印:把编号为i的圆盘从M位置移动到N位置
sum += 1;
cout << "编号为 " << i << " 的圆盘从 " << M << " 移动到 " << N << ";" << " 第 " << sum << " 次移动" << endl;
}
void Hannoi(int n, char W1, char W2, char W3)
{
if (n == 0)
{
cout << "没有圆盘,不需要移动";
}
else if (n == 1)
{//如果只有一个圆盘,那么直接从A移动到B
Move(1, W1, W2);
return;
}
else
{
Hannoi(n - 1, W1, W3, W2);//考虑A上面的n-1个圆盘是怎么从A移动到C的
Move(n, W1, W2);//第n个从A到B
Hannoi(n - 1, W3, W2, W1);//考虑C上面的n-1个圆盘怎么从C移动到B上
}
}
int main()
{
int n;
cout << "请输入圆盘数量:";
cin >> n;
Hannoi(n, 'A', 'B', 'C');
return 0;
}
文章来源:https://blog.csdn.net/qq_41422262/article/details/132752860
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- PR、希喂、百利主食冻干哪款更好?铲龄8年真实喂养测评
- 【C语言】ipoib驱动 - ipoib_cm_post_receive_srq_rss函数
- 【Python学习笔记】读取Matlab数据文件
- 数据结构-B树删除示例
- 用java语言写一个协同过滤算法
- 【uniapp】APP打包上架应用商-注意事项
- mongodb 安装
- PostGIS学习教程十六:几何图形的相等
- 深度解析 Compose 的 Modifier 原理 -- Modifier、CombinedModifier
- 开发运营微信小游戏怎么才能盈利呢?