【MATLAB】 SSA奇异谱分析信号分解算法

有意向获取代码，请转文末观看代码获取方式~

1 基本定义

SSA奇异谱分析（Singular Spectrum Analysis）是一种处理非线性时间序列数据的方法，可以对时间序列进行分析和预测。

它基于构造在时间序列上的特定矩阵的奇异值分解（SVD），可以从一个时间序列中分解出趋势、振荡分量和噪声。

具体流程如下：

1. 根据原始时间序列构建轨迹矩阵X XX。

2. 对矩阵X进行奇异值分解：X = ∑ i = 1 r σ i U i V i T X=\sum_{i=1}^{r} \sigma_i U_i V_{i}^TX=∑i=1r?σi?Ui?ViT? 。

3. 按奇异值生成r rr个子矩阵:X i = σ i U i V i T X_i = \sigma_i U_i V_{i}^TXi?=σi?Ui?ViT? 。

4. 根据某一分组原则将子矩阵X i X_iXi?分为m mm个组。

5. 对子矩阵X i X_iXi?进行对角均值化处理得到子序列。

6. 对m mm个组中的子序列相加得到分组子序列。

以上就是SSA奇异谱分析信号分解算法的基本步骤。

2 出图效果

附出图效果如下：

Toeplitz 法计算的协方差矩阵 C

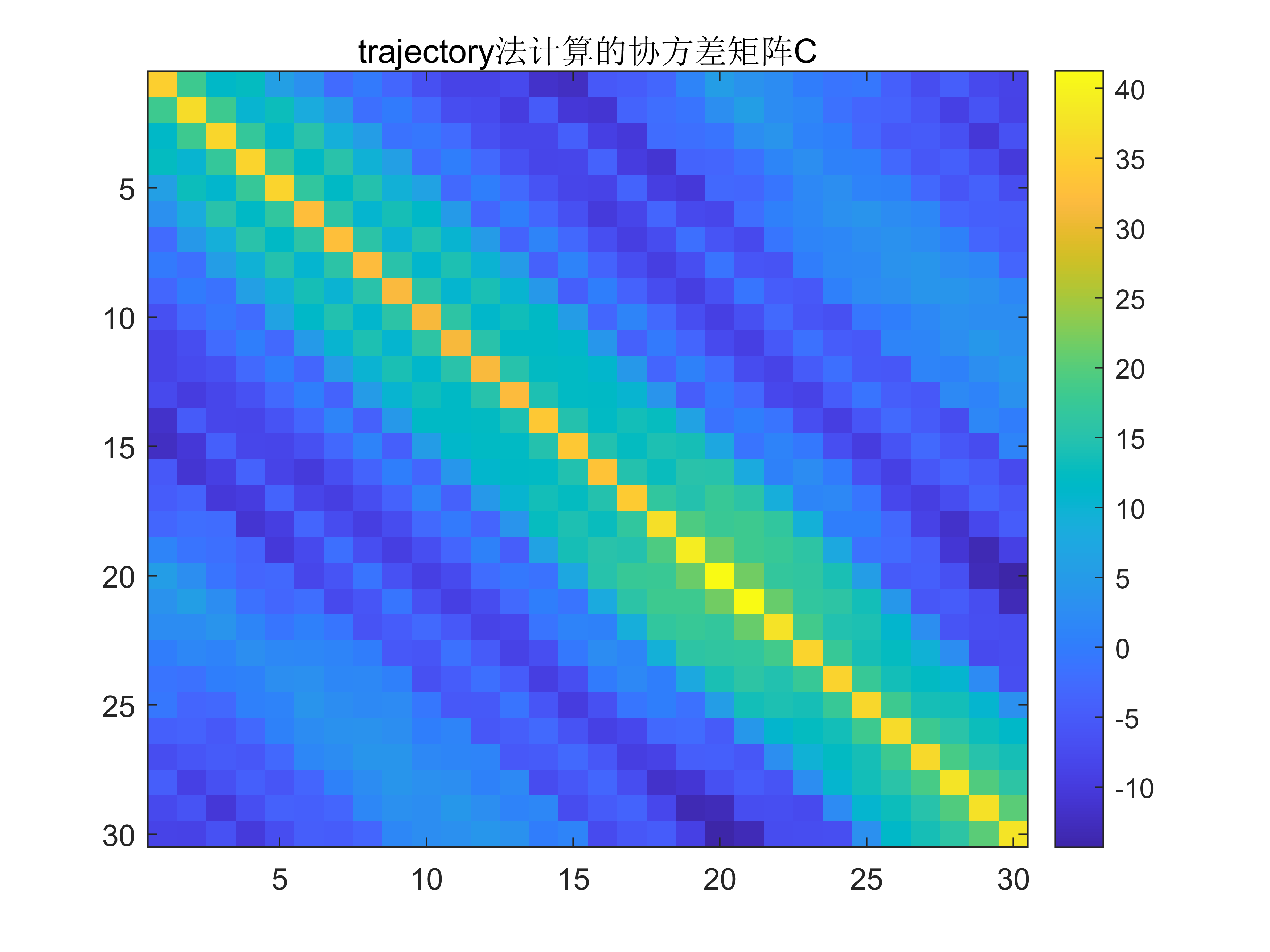
trajectory法计算的协方差矩阵C

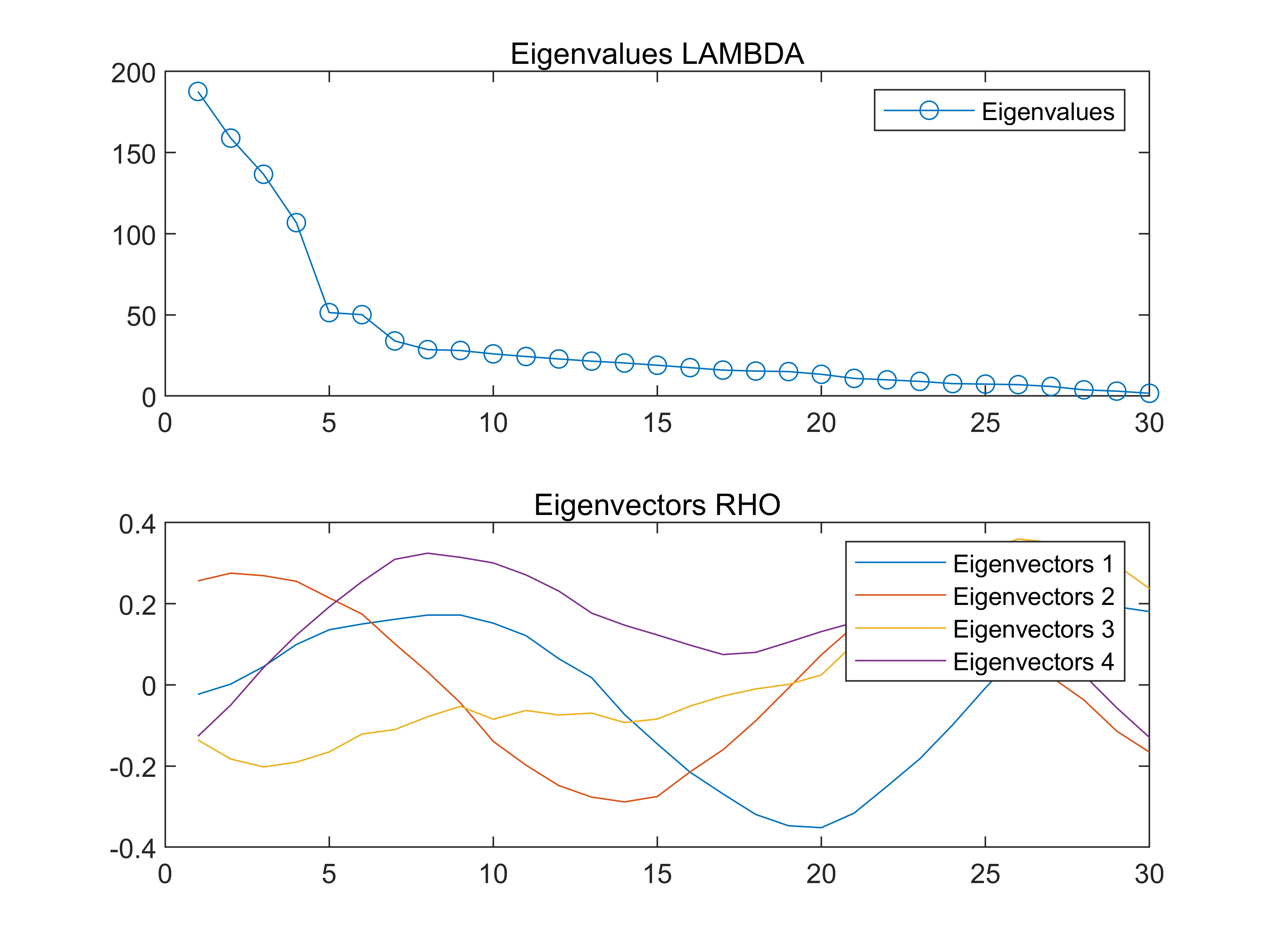
特征值和特征向量示意图

前四大主成分

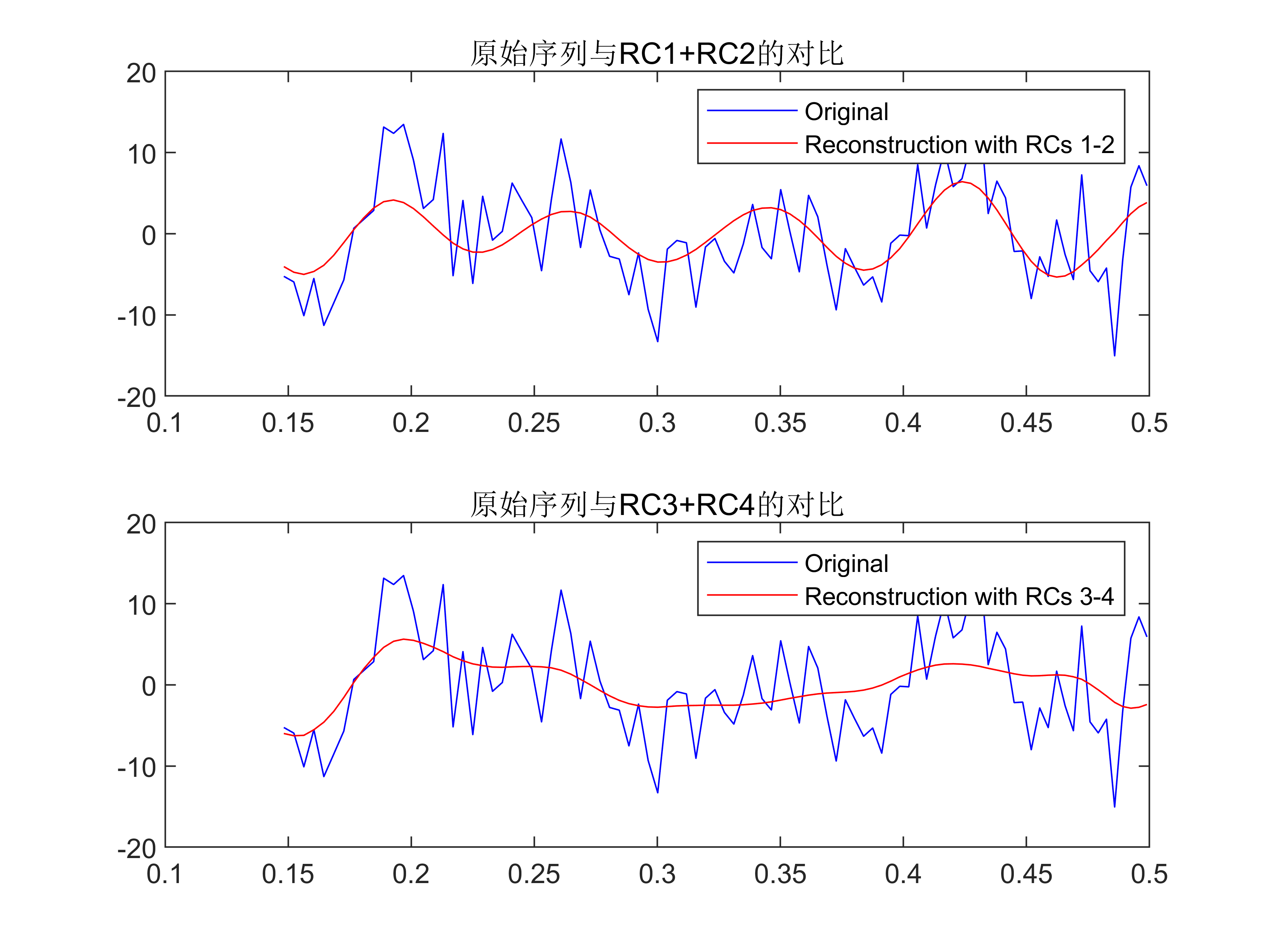
前四大重构成分

重建和原始时间序列对比