顺时针打印矩阵：偏移量法与边界控制法比较---剑指offer-JZ29 顺时针打印矩阵

?在编程中，处理二维数组的问题可以有多种解法。今天，我们将探讨两种解决“顺时针打印矩阵”问题的方法：偏移量法和边界控制法，并进行比较。

题目

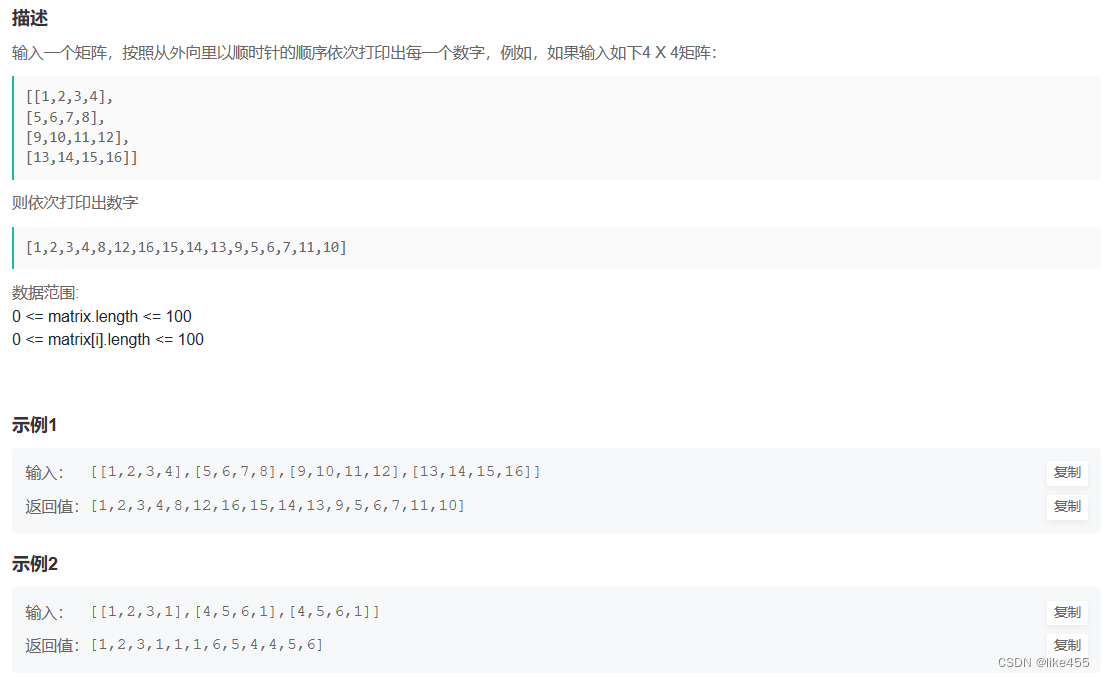
题目连接：顺时针打印矩阵_牛客题霸_牛客网 (nowcoder.com)

偏移量法

偏移量法的核心思想是使用两个数组来控制遍历方向。这种方法特别适合于遍历二维空间时的方向控制。

代码实现

import java.util.ArrayList;
import java.util.List;

public class Solution {
    // 定义dx和dy为静态数组，表示四个方向的偏移量：上，右，下，左
    private static final int[] dx = {-1, 0, 1, 0};
    private static final int[] dy = {0, 1, 0, -1};

    public List<Integer> printMatrix(int[][] matrix) {
        List<Integer> res = new ArrayList<>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return res;

        int n = matrix.length, m = matrix[0].length;
        boolean[][] st = new boolean[n][m]; // st数组用于标记已访问的位置

        int x = 0, y = 0, d = 1; // 初始位置(0,0)和方向(向右)
        for (int k = 0; k < n * m; k++) {
            res.add(matrix[x][y]); // 添加当前元素
            st[x][y] = true; // 标记为已访问

            // 计算下一个位置
            int a = x + dx[d], b = y + dy[d];
            // 判断边界和是否已访问
            if (a < 0 || a >= n || b < 0 || b >= m || st[a][b]) {
                d = (d + 1) % 4; // 改变方向
                a = x + dx[d];
                b = y + dy[d];
            }
            x = a;
            y = b;
        }
        return res;
    }
}

解释：

偏移量按照“上、右、下、左”的顺序来定义的。这个顺序决定了遍历矩阵的方向。

在代码中：

• dx = {-1, 0, 1, 0} 表示行的变化。

• dy = {0, 1, 0, -1} 表示列的变化。

这里的偏移量对应的遍历方向是：

1. 向上（dx = -1, dy = 0）。

2. 向右（dx = 0, dy = 1）。

3. 向下（dx = 1, dy = 0）。

4. 向左（dx = 0, dy = -1）。

在遍历过程中，通过改变d的值来选择不同的偏移量，从而改变遍历的方向。遍历始于向右方向（d = 1），并在遇到边界或已访问的元素时顺时针旋转到下一个方向。

这种方法特别适合处理这类二维数组遍历的问题。通过简单地调整偏移量数组，可以轻松地更改遍历的方向或模式，适应各种不同的需求和场景。

如何定义dx、dy数组？

矩阵遍历使用的x和y的定义有些特殊。通常，在数学和计算机图形学中，我们习惯于将x轴定义为水平方向，y轴定义为垂直方向。然而，在二维数组或矩阵的上下文中，这些轴的定义通常与传统的笛卡尔坐标系有所不同。

在代码中

• x变量代表的是二维数组的行索引。

• y变量代表的是二维数组的列索引。

然而，

• 当我们说“向上”移动时，实际上是在减少x的值（因为在数组中向上移动意味着向更小的行索引移动）。

• 同样，"向右"移动实际上是增加y的值（在数组中向右移动意味着向更大的列索引移动）。

• “向下”移动是增加x的值。

• “向左”移动是减少y的值。

这种定义方式是基于二维数组的索引，其中matrix[x][y]表示位于第x行和第y列的元素。所以，尽管这种定义方式可能与传统的笛卡尔坐标系不同，但它完全适合于二维数组或矩阵的遍历操作。

我的这篇? 使用邻接点偏移量数组解决 BFS 类问题-CSDN博客??博客同样讲解了这类问题

优势与局限性

优势：

1. 代码简洁：整个遍历过程可以在一个循环中完成。

2. 方向控制灵活：通过改变索引即可改变方向，适用于复杂路径的遍历。

局限性：

1. 需要额外状态数组：用于记录哪些元素已被访问。

2. 边界处理稍复杂：需要检查下一个位置是否越界或已访问。

---

边界控制法

边界控制法通过定义上下左右边界来控制遍历过程。

代码实现

import java.util.ArrayList;
public class Solution {
    public ArrayList<Integer> printMatrix(int [][] matrix) {
        ArrayList<Integer> res = new ArrayList<>();
         //先排除特殊情况
        if(matrix.length == 0) {
            return res;
        }
        //左边界
        int left = 0; 
        //右边界
        int right = matrix[0].length - 1; 
        //上边界
        int up = 0; 
        //下边界
        int down = matrix.length - 1; 
        //直到边界重合
        while(left <= right && up <= down){ 
            //上边界的从左到右
            for(int i = left; i <= right; i++) 
                res.add(matrix[up][i]); 
            //上边界向下
            up++; 
            if(up > down)
                break;
            //右边界的从上到下
            for(int i = up; i <= down; i++) 
                res.add(matrix[i][right]);
            //右边界向左
            right--; 
            if(left > right)
                break;
            //下边界的从右到左
            for(int i = right; i >= left; i--) 
                res.add(matrix[down][i]);
            //下边界向上
            down--; 
            if(up > down)
                break; 
            //左边界的从下到上
            for(int i = down; i >= up; i--) 
                res.add(matrix[i][left]);
            //左边界向右
            left++; 
            if(left > right)
                break;
        }
        return res;
    }
}

优势与局限性

优势：

1. 直观明了：逻辑清晰，易于理解和维护。

2. 无需额外状态数组：直接通过边界控制实现遍历。

局限性：

1. 多个循环：每个方向的遍历需要独立的循环。

2. 边界更新逻辑：每完成一个方向，都需要更新边界。

总结

两种方法各有优缺点。偏移量法在代码简洁性和灵活性方面更优，但需要额外的状态数组来跟踪已访问的元素。边界控制法则在逻辑清晰度上占优，但涉及多个循环和边界更新的逻辑。

就我各个人来讲。把算法题抽象成通用模板确实可以提高解题效率，特别是对于那些有固定模式或可复用逻辑的问题。使用偏移量方法解决矩阵遍历类问题是一个很好的例子。这种方法不仅提供了一种清晰、灵活的方式来处理二维空间的遍历，还可以轻松应对多种不同的遍历要求，比如螺旋遍历、波形遍历等。

偏移量法的模板化

偏移量法的核心在于定义一组方向向量，通过这些向量控制遍历的方向。这种方法的模板化可以分为以下几个步骤：

1. 定义方向向量：创建两个数组，一个表示行的偏移（dx），另一个表示列的偏移（dy）。例如，对于上、右、下、左的顺时针方向，可以定义dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1}。

2. 初始化遍历状态：设置起始点和初始方向，通常从(0,0)点开始，方向设置为向右。

3. 遍历矩阵：使用一个循环进行遍历，每次移动后检查边界和是否已访问，必要时改变方向。

4. 边界和访问状态检查：在每次移动后，检查下一个位置是否超出矩阵边界或者已经访问过。如果是，改变方向。

这种模板化方法在处理各种矩阵遍历问题时具有明显优势：

• 可重用性：一旦掌握了这个模板，就可以快速应用到类似的问题上。
• 灵活性：通过调整方向向量，可以轻松适应不同的遍历要求。
• 简洁性：代码更加简洁，易于理解和维护。