C语言归并排序（合并排序）算法以及代码

合并排序是采用分治法，先将无序序列划分为有序子序列，再将有序子序列合并成一个有序序列的有效的排序算法。

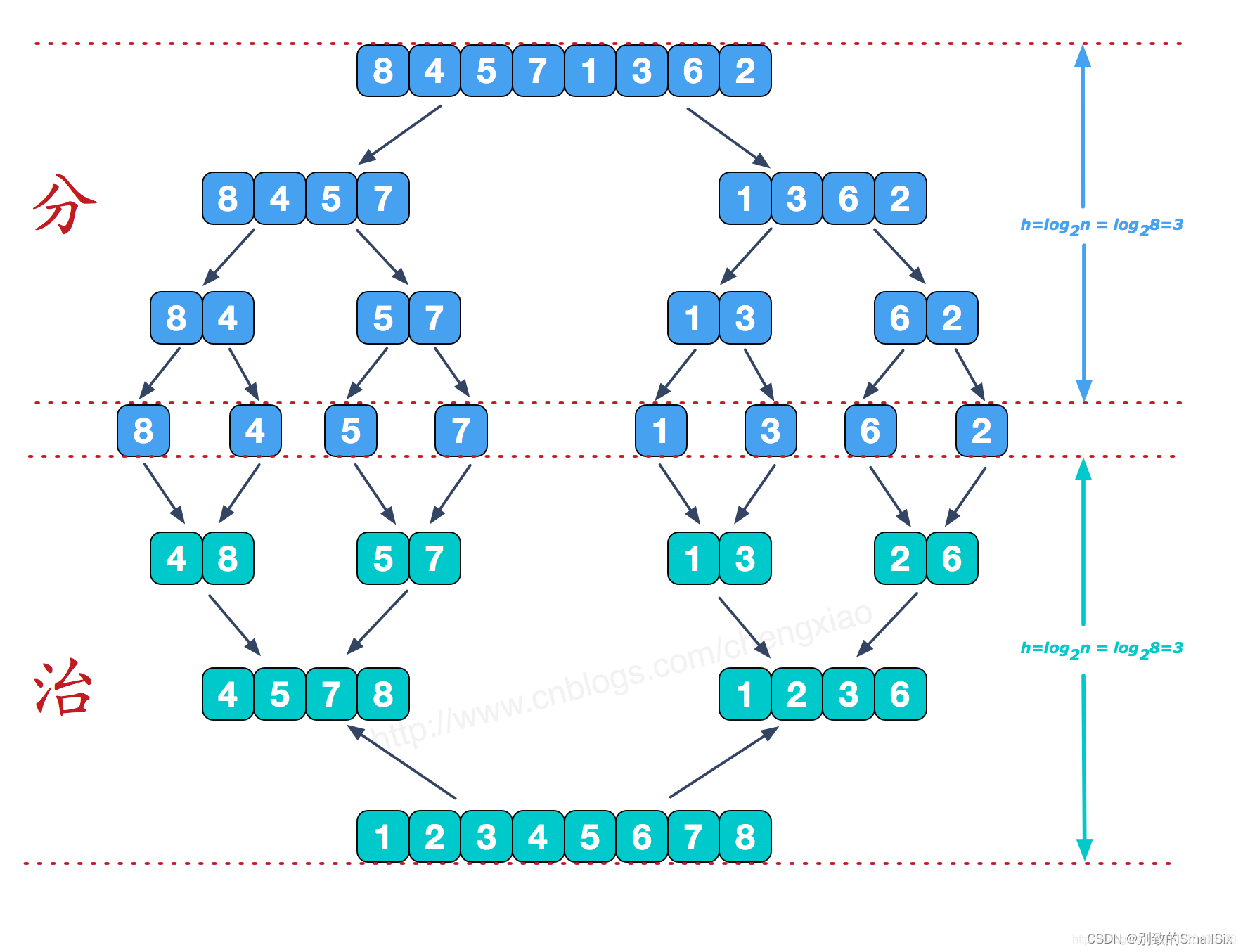
原理：先将无序序列利用二分法划分为子序列，直至每个子序列只有一个元素(单元素序列必有序)，然后再对有序子序列逐步(两两)进行合并排序。合并方法是循环的将两个有序子序列当前的首元素进行比较，较小的元素取出，置入合并序列的左边空置位，直至其中一个子序列的最后一个元素置入合并序列中。最后将另一个子序列的剩余元素按顺序逐个置入合并序列尾部即可完成排序。整体过程如下图：

?两个有序子序列合并的原理如下图：

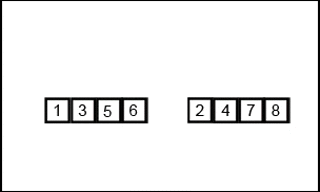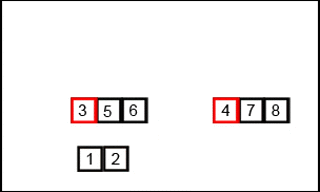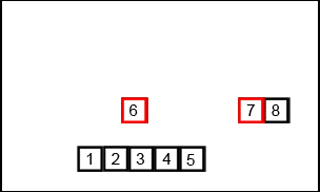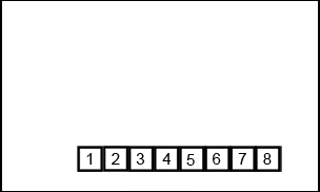
代码：递归式实现

#include <malloc.h>
#include <stdlib.h>
void mergesort(int A[],int n)  //合并排序的递归主体
{
    void merge(int A[], int L[], int R[], int l, int r);  //声明merge函数
    if(n>1)    //多于一个元素才需要排序
    {
        int mid=n/2;
        int *left=(int*)malloc(sizeof(int)*mid);
        int *right=(int*)malloc(sizeof(int)*(n-mid));
        for(int i=0;i<mid;i++)
            left[i]=A[i];       //建立临时数组存储左半部分序列
        for(int j=mid;j<n;j++)
            right[j-mid]=A[j];  //建立临时数组存储右半部分序列
 
        mergesort(left,mid);    //调用自身对左半部分进行合并排序
        mergesort(right,n-mid); //调用自身对右半部分进行合并排序
        merge(A,left,right,mid,n-mid);   //两个有序序列的合并操作，封装为函数
        free(left);
        free(right);
    }
}
 
void merge(int A[],int L[],int R[],int l,int r)  //两个有序序列L、R合并为A，l,r分别为L,R的长度
{
    int i=0,j=0,k=0;
    while(i<l&&j<r)  //两个子序列首元素做比较，小者取出置入父序列
    {
        if(L[i]<=R[j])
            A[k++]=L[i++];
        else
            A[k++]=R[j++];
    }
    while(i<l)       //将左半部分剩余元素置入父序列
    {
        A[k++]=L[i++];
    }
    while(j<r)       //将右半部分剩余元素置入父序列
    {
        A[k++]=R[j++];
    }
}

改进：非递归式实现

递归式的实现方法，当输入规模增大时，会表现出效率低的缺点。且在排序过程中会不断的开辟临时空间，容易造成内存混乱。

void mergesort(int A[], int n){    //非递归实现。只开辟一个大小与待排序数组相同的存储数组，排序过程中直接在该数组上进行操作。不反复开辟临时数组
	int step;   
	int *p, *q, *t;
	int i, j, k, len1, len2;
	int *temp;  
	step = 1;      //初始步长为1，即将单个元素作为有序子序列进行合并
	p = A;
	q = (int*)malloc(sizeof(int)*n);  //q为临时开辟的空间，用来存储已排序序列，大小为待排序数组的长度
	temp = q;                              //temp与q指向同一段内存，留作最后释放内存空间时使用，因为q指针在后面排序操作中可能会改变指向
	while (step<n)
	{
		i = 0;
		j = i + step;
		k = i;                             //k用作临时数组的下标
		len1 = i + step < n ? i + step : n;   //len1表示有序序列1的下标上限
		len2 = j + step < n ? j + step : n;   //len2表示有序序列2的下标上限
		while (i<n)
		{
			while (i<len1&&j<len2)        //两个子序列首元素做比较，小者取出置入父序列
			{
				q[k++] = p[i]<p[j] ? p[i++] : p[j++];
			}
			while (i<len1)                //将子序列1的剩余元素置入父序列
			{
				q[k++] = p[i++];
			}
			while (j<len2)                //将子序列2的剩余元素置入父序列
			{
				q[k++] = p[j++];
			}
			i = j;                        //j经过自增变为len2，然后赋值给i
			j = i + step;                 //i被赋值为len2,加上步长再赋值给j
			k = i;                        
			len1 = i + step < n ? i + step : n;
			len2 = j + step < n ? j + step : n;
		}
		step *= 2;   //步长翻倍，即将原步长2倍个数的数组元素作为有序子序列进行合并
		t = p;       //t作为临时指针变量，用于交换p和q的指针指向
		p = q;       //将p指针指向经过一轮合并排序后的临时数组
		q = t;       //将q指针指向原数组
	}
	if (A != p){     //如果最终p指针的指向改变为临时数组，则将完成排序的数组拷贝至原数组
		memcpy(A, p, sizeof(int)*n);
	}
	free(temp);
}