代码随想录算法训练营第59天| 503.下一个更大元素II 42. 接雨水

java代码编写

503.下一个更大元素II

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。

数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

示例 1:

输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

示例 2:

输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]

提示:

• 1 <= nums.length <= 104
• -109 <= nums[i] <= 109

教程：https://programmercarl.com/0503.%E4%B8%8B%E4%B8%80%E4%B8%AA%E6%9B%B4%E5%A4%A7%E5%85%83%E7%B4%A0II.html

方法一：暴力解法

思路：和739. 每日温度的暴力解法差不多，区别是这里要循环找下一个比当前大的。

区别就是默认填充-1，第二个循环要进行循环遍历。

内循环j的范围调整为i+n，下标通过对n取余遍历到前面的索引。

力扣上可以通过，执行90ms，内存44.76MB。

复杂度分析：

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n)$

class Solution {
    public int[] nextGreaterElements(int[] nums) {
        int n = nums.length;
        int[] res = new int[n];
        Arrays.fill(res, -1); // 填充res数组为-1

        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < i + n; j++) {
                int index = j % n; // 通过取余实现循环数组
                if (nums[index] > nums[i]) {
                    res[i] = nums[index];
                    break;
                }
            }
        }
        return res;
    }
}

方法二：单调栈

思路：和方法一有相似之处，都是使用取余的方式来控制循环找比当前大的下标。

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

import java.util.Arrays;
import java.util.Stack;

class Solution {
    public int[] nextGreaterElements(int[] nums) {
        //边界判断
        if(nums == null || nums.length <= 1) {
            return new int[]{-1};
        }
        int n = nums.length;
        int[] result = new int[n];//存放结果
        Arrays.fill(result,-1);//默认全部初始化为-1
        int a=0;
        Stack<Integer> st= new Stack<>();//栈中存放的是nums中的元素下标
        for(int i = 0; i < 2*n; i++) {
            while(!st.empty() && nums[i % n] > nums[st.peek()]) {
                a = st.peek();
                System.out.println(a);
                result[st.peek()] = nums[i % n];//更新result
                st.pop();//弹出栈顶
            }
            st.push(i % n);
        }
        return result;
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        int[] result = solution.nextGreaterElements(new int[]{1,2,1});
        for (int num : result) {
            System.out.print(num + " ");
        }
    }
}

这里利用栈的特性，拿nums = [1,2,1]为例子说，

i=0时，首先将下标0放入栈；

i=1时，栈非空，num[1]>nums[栈顶元素]也就是nums[1]>nums[0],是的2>1,所以result[0]=nums[1]=2,将栈顶元素0出栈，此时栈为空，将1再入栈；

i=2时，栈非空，num[2]>nums[栈顶元素]也就是nums[2]>nums[1],是的1>2,假的，所以将2入栈，此时栈中元素为1,2；

i=3时，栈非空，num[3%3]>nums[栈顶元素]也就是nums[0]>nums[2],是的1>1,假的，所以将0入栈，此时栈中元素为1,2,0；

i=4时，栈非空，num[4%3]>nums[栈顶元素]也就是nums[1]>nums[0],是的2>1,真的，所以result[栈顶元素]=result[0]=nums[1]=2,将栈顶元素0出栈;num[4%3]>nums[栈顶元素]也就是nums[1]>nums[2],是的2>1,真的， 所以result[栈顶元素]=result[2]=nums[1]=2,将栈顶元素2出栈;num[4%3]>nums[栈顶元素]也就是nums[1]>nums[1],退出while循环，将1入栈，此时栈中元素为1,1；

i=5时，栈非空，num[5%3]>nums[栈顶元素]也就是nums[2]>nums[1],是的1>2,假的，所以将2入栈，此时栈中元素为1,1,2；

i<6退出循环，结束，此时result=[2,-1,2].

看看栈的特性，又有点忘了

import java.util.Stack;

public class StackExample {
    public static void main(String[] args) {
        // 创建一个整数类型的栈
        Stack<Integer> stack = new Stack<>();

        // 将元素压入栈顶
        stack.push(10);
        stack.push(20);
        stack.push(30);

        // 查看栈顶元素
        System.out.println("栈顶元素：" + stack.peek()); // 输出：30

        // 弹出栈顶元素
        int poppedElement = stack.pop();
        System.out.println("弹出的栈顶元素：" + poppedElement); // 输出：30

        // 查看栈顶元素（此时栈顶元素为20）
        System.out.println("栈顶元素：" + stack.peek()); // 输出：20

        // 判断栈是否为空
        System.out.println("栈是否为空：" + stack.isEmpty()); // 输出：false

        // 获取栈的大小
        System.out.println("栈的大小：" + stack.size()); // 输出：2

        // 遍历栈元素
        System.out.print("栈中的元素：");
        while (!stack.isEmpty()) {
            System.out.print(stack.pop() + " ");
        }
        // 输出：20 10

        // 栈现在为空
        System.out.println("\n栈是否为空：" + stack.isEmpty()); // 输出：true
    }
}

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

教程：https://programmercarl.com/0042.%E6%8E%A5%E9%9B%A8%E6%B0%B4.html

方法一：暴力解法

思路：两个循环，关键我想不出正常的解题思路。这个在力扣上超时。

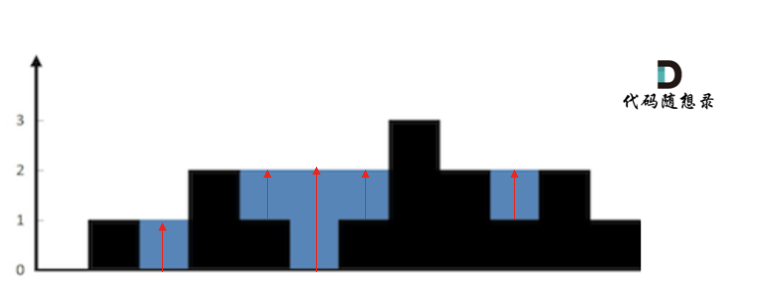
首先，如果按照列来计算的话，宽度一定是1了，我们再把每一列的雨水的高度求出来就可以了。

可以看出每一列雨水的高度，取决于，该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。

来举一个理解，例如求列4的雨水高度，如图：

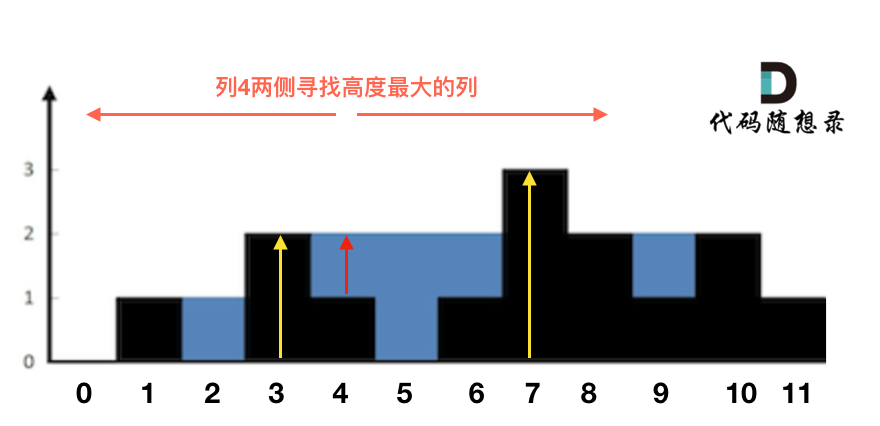
复杂度分析：

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

class Solution {
    public int trap(int[] height) {
        int sum = 0;
        for (int i = 0; i < height.length; i++) {
            // 第一个柱子和最后一个柱子不接雨水
            if (i==0 || i== height.length - 1) continue;

            int rHeight = height[i]; // 记录右边柱子的最高高度
            int lHeight = height[i]; // 记录左边柱子的最高高度

            for (int r = i+1; r < height.length; r++) {
                if (height[r] > rHeight) rHeight = height[r];
            }
            for (int l = i-1; l >= 0; l--) {
                if(height[l] > lHeight) lHeight = height[l];
            }
            int h = Math.min(lHeight, rHeight) - height[i];
            if (h > 0) sum += h;
        }
        return sum;
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        int sum = solution.trap(new int[]{4,2,0,3,2,5});
        System.out.println(sum);
    }
}

方法二：双指针法

思路：就是暴力解法的升级版。在暴力解法的基础上，直接将每个i的左侧最高的柱子和右侧最高的柱子存入数组，减少遍历次数，用的时候直接拿。

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

class Solution {
    public int trap(int[] height) {
        int length = height.length;
        if (length <= 2) return 0;
        int[] maxLeft = new int[length];
        int[] maxRight = new int[length];

        // 记录每个柱子左边柱子最大高度
        maxLeft[0] = height[0];
        for (int i = 1; i< length; i++) maxLeft[i] = Math.max(height[i], maxLeft[i-1]);

        // 记录每个柱子右边柱子最大高度
        maxRight[length - 1] = height[length - 1];
        for(int i = length - 2; i >= 0; i--) maxRight[i] = Math.max(height[i], maxRight[i+1]);

        // 求和
        int sum = 0;
        for (int i = 0; i < length; i++) {
            int count = Math.min(maxLeft[i], maxRight[i]) - height[i];
            if (count > 0) sum += count;
        }
        return sum;
    }
}

方法三：单调栈

思路：给我我是想不起来用单调栈的。

单调栈就是保持栈内元素有序。和栈与队列：单调队列 (opens new window)一样，需要我们自己维持顺序，没有现成的容器可以用。

1.单调栈是按照行方向来计算雨水，如图：

2.使用单调栈内元素的顺序

从大到小还是从小到大呢？

从栈头（元素从栈头弹出）到栈底的顺序应该是从小到大的顺序。

因为一旦发现添加的柱子高度大于栈头元素了，此时就出现凹槽了，栈头元素就是凹槽底部的柱子，栈头第二个元素就是凹槽左边的柱子，而添加的元素就是凹槽右边的柱子。

3.遇到相同高度的柱子怎么办。

遇到相同的元素，更新栈内下标，就是将栈里元素（旧下标）弹出，将新元素（新下标）加入栈中。

例如 5 5 1 3 这种情况。如果添加第二个5的时候就应该将第一个5的下标弹出，把第二个5添加到栈中。

因为我们要求宽度的时候 如果遇到相同高度的柱子，需要使用最右边的柱子来计算宽度。

4.栈里要保存什么数值

使用单调栈，也是通过 长 * 宽 来计算雨水面积的。

长就是通过柱子的高度来计算，宽是通过柱子之间的下标来计算，

那么栈里有没有必要存一个pair<int, int>类型的元素，保存柱子的高度和下标呢。

其实不用，栈里就存放下标就行，想要知道对应的高度，通过height[stack.top()] 就知道弹出的下标对应的高度了。

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

class Solution {
    public int trap(int[] height){
        int size = height.length;

        if (size <= 2) return 0;

        // in the stack, we push the index of array
        // using height[] to access the real height
        Stack<Integer> stack = new Stack<Integer>();
        stack.push(0);

        int sum = 0;
        for (int index = 1; index < size; index++){
            int stackTop = stack.peek();
            if (height[index] < height[stackTop]){
                stack.push(index);
            }else if (height[index] == height[stackTop]){
                // 因为相等的相邻墙，左边一个是不可能存放雨水的，所以pop左边的index, push当前的index
                stack.pop();
                stack.push(index);
            }else{
                //pop up all lower value
                int heightAtIdx = height[index];
                while (!stack.isEmpty() && (heightAtIdx > height[stackTop])){
                    int mid = stack.pop();

                    if (!stack.isEmpty()){
                        int left = stack.peek();

                        int h = Math.min(height[left], height[index]) - height[mid];
                        int w = index - left - 1;
                        int hold = h * w;
                        if (hold > 0) sum += hold;
                        stackTop = stack.peek();
                    }
                }
                stack.push(index);
            }
        }
        return sum;
    }
}