二进制、八进制、十六进制的转换

进制转换

进制转换是人们利用符号来技术的方法。

进制转换由一组数码符号和两个基本因素“基数”与“位权”构成。

基数是指，进位计数制中所采用的数码（数制中用来表示“量”的符号）的个数。

位权是指，进位制中每一固定位置对应的单位值。

在知乎有个问题下的解答很不错，可以参考：打开链接

他们之间的关系如下：

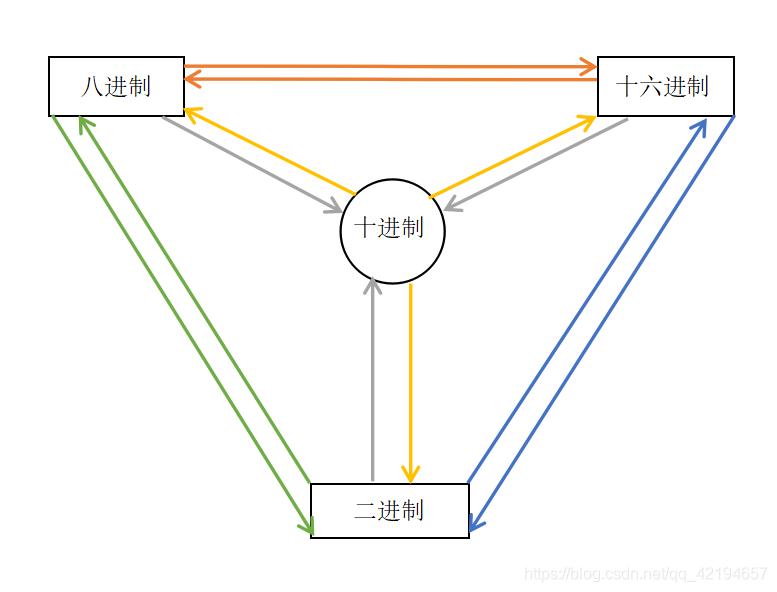
（二，八，十六进制）转十进制

方法：假设我们要将n进制转换为十进制，首先我们从n进制的右边为第一位数（从低位到高位），其权值是n的0次方，第二位是n的1次方，依次递增下去，把最后的结果相加的值就是十进制的值了。

举个例子：将（1101）n 转换为十进制

（1101）n = 1*（n）^3 + 1 * (n) ^ 2 + 0 * (n) ^ 1 + 0 * (n) ^ 0 ;

如：(1101) 2 = 1*（2）^3 + 1 * (2) ^ 2 + 0 * (2) ^ 1 + 1 * (2) ^ 0 = 13;

八进制，十六进制同样如此。

例：将十六进制的 96 转换为十进制的步骤如下：

( 96 )16 = 6 * (16) ^ 0 + 9 * (16) ^ 1 = 6 + 144 = 150

将八进制的 226 转换为十进制的步骤如下：

( 226 )8 = 6 * (8) ^ 0 + 2 * (8) ^ 1 + 2 * (8) ^ 2 = 6 + 16 + 128 = 150

公式提取

（自右向左为第-an、-a(n-1)、 … 、-a3 、-a2、-a1、a1、a2、a3、… 、a(n-1)、an位数–注意这里没有a0，-a1至-an为小数点后的第1位到第n位，设当前进制为x ）
(十进制) = [小数点之后第一位到第n位] + [小数点之前个位数、十位数、…]
= [ -a1 * x ^ -1 + -a2 * x ^ -2 + … + -an * x ^ -n] + [a1 * x ^ 0 + a2 * x ^ 1 + a3 * x ^ 2 + … + a(n-1) * x ^ (n-2) + an * x ^ (n-1)]

十进制 转换为（二，八，十六进制）

假设我们要将十进制转换为n进制

方法：除n取余法，即每次将整数部分除以n，余数为该位权上的数，而商继续除以n，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数。

例：将十进制的(796)D转换为十六进制的步骤如下：

1. 将商796除以16，商49余数为12，对应十六进制的C；

2. 将商49除以16，商3余数为1；

3. 将商3除以16，商0余数为3；

#（二进制） ? （八、十六进制）

二进制 → 八进制

方法：取三合一法，即从二进制的小数点为分界点，向左（向右）每三位取成一位，接着将这三位二进制按权相加，然后，按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的八进制数。如果向左（向右）取三位后，取到最高（最低）位时候，如果无法凑足三位，可以在小数点最左边（最右边），即整数的最高位（最低位）添0，凑足三位。
　　
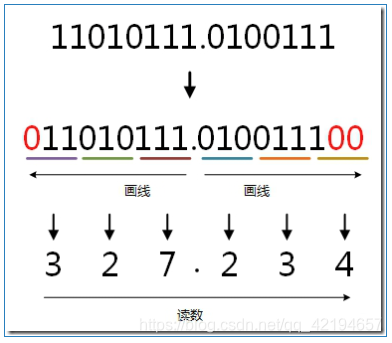
例：将二进制的(11010111.0100111)B转换为八进制的步骤如下：

1. 小数点前111 = 7；

2. 010 = 2；

3. 11补全为011，011 = 3；

4. 小数点后010 = 2；

5. 011 = 3；

6. 1补全为100，100 = 4；

7. 读数，读数从高位到低位，即(11010111.0100111)B=(327.234)O。

二进制与八进制编码对应表：

二进制	八进制
000	0
001	1
010	2
011	3
100	4
101	5
110	6
111	7

八进制 → 二进制

方法：取一分三法，即将一位八进制数分解成三位二进制数，用三位二进制按权相加去凑这位八进制数，小数点位置照旧。

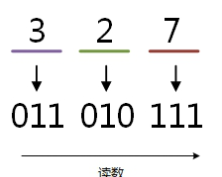
例：将八进制的(327)O转换为二进制的步骤如下：

1. 3 = 011；

2. 2 = 010；

3. 7 = 111；

4. 读数，读数从高位到低位，011010111，即(327)O=(11010111)B。

二进制 → 十六进制

方法：取四合一法，即从二进制的小数点为分界点，向左（向右）每四位取成一位，接着将这四位二进制按权相加，然后，按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的十六进制数。如果向左（向右）取四位后，取到最高（最低）位时候，如果无法凑足四位，可以在小数点最左边（最右边），即整数的最高位（最低位）添0，凑足四位。

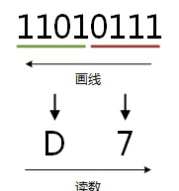
例：将二进制的(11010111)B转换为十六进制的步骤如下：

1. 0111 = 7；

2. 1101 = D；

3. 读数，读数从高位到低位，即(11010111)B=(D7)H。

十六进制 → 二进制

方法：取一分四法，即将一位十六进制数分解成四位二进制数，用四位二进制按权相加去凑这位十六进制数，小数点位置照旧。

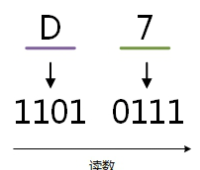
例：将十六进制的(D7)H转换为二进制的步骤如下：

1. D = 1101；

2. 7 = 0111；

3. 读数，读数从高位到低位，即(D7)H=(11010111)B。

八进制 → 十六进制**

方法：将八进制转换为二进制，然后再将二进制转换为十六进制，小数点位置不变。

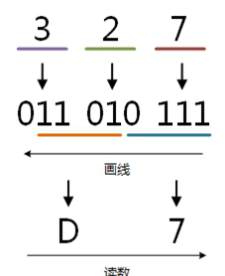
例：将八进制的(327)O转换为十六进制的步骤如下：

1. 3 = 011；

2. 2 = 010；

3. 7 = 111；

4. 0111 = 7；

5. 1101 = D；

6. 读数，读数从高位到低位，D7，即(327)O=(D7)H。

十六进制 → 八进制

方法：将十六进制转换为二进制，然后再将二进制转换为八进制，小数点位置不变。

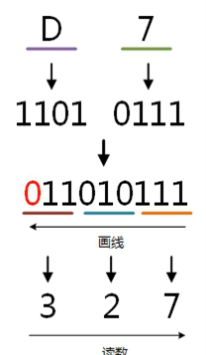
例：将十六进制的(D7)H转换为八进制的步骤如下：

1. 7 = 0111；

2. D = 1101；

3. 0111 = 7；

4. 010 = 2；

5. 011 = 3；

6. 读数，读数从高位到低位，327，即(D7)H=(327)O。

扩展

负数的进制转换稍微有些不同。

先把负数写为其补码形式（在此不议），然后再根据二进制转换其它进制的方法进行。

包含小数的进制换算：

(ABC.8C)H=10x16^2+11x161+12x16^0+8x16-1+12x16^-2

=2560+176+12+0.5+0.046875

=(2748.546875)D

转载自：https://www.cnblogs.com/gaizai/p/4233780.html