【动画图解】一次理清九大排序算法！面试官问到再也不慌！

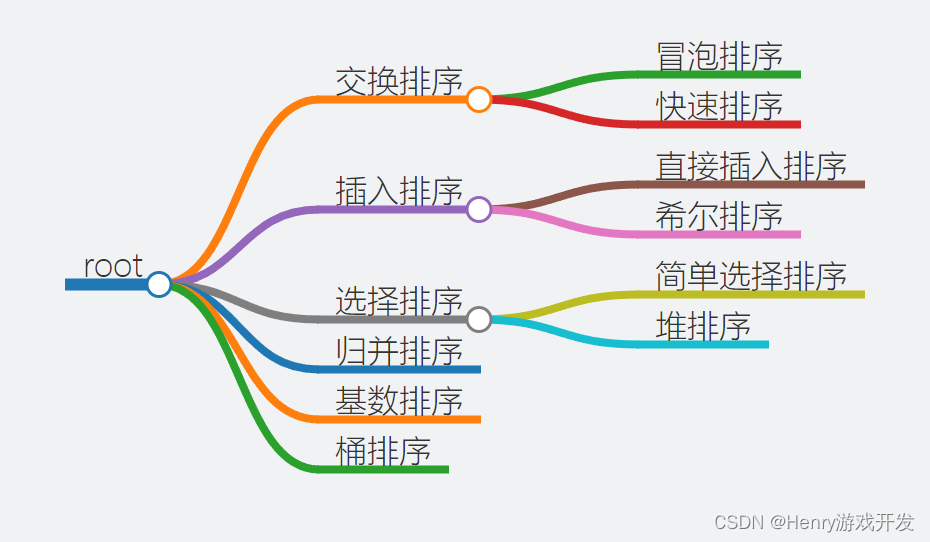
排序算法

• 交换排序
  • 冒泡排序
  • 快速排序
• 插入排序
  • 直接插入排序
  • 希尔排序
• 选择排序
  • 简单选择排序
  • 堆排序
• 归并排序
• 基数排序
• 桶排序
  

一、冒泡排序

冒泡排序是一种简单的交换排序算法，以升序排序为例，其核心思想是：

1. 从第一个元素开始，比较相邻的两个元素。如果第一个比第二个大，则进行交换。
2. 轮到下一组相邻元素，执行同样的比较操作，再找下一组，直到没有相邻元素可比较为止，此时最后的元素应是最大的数。
3. 除了每次排序得到的最后一个元素，对剩余元素重复以上步骤，直到没有任何一对元素需要比较为止。

/**
 * 冒泡排序
 *
 * @param arr
 */
public void bubbleSort(int[] arr) {
    int tmp;
    // 冒泡优化：如果在某一次冒泡过程中，没有发生交换，则证明数组已经是有序的了
    for (int i = 0; i < arr.length; i++) {
        boolean flag = true;
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[j] < arr[i]) {
                flag = false;
                tmp = arr[j];
                arr[j] = arr[i];
                arr[i] = tmp;
            }
        }
        if (flag) {
            break;
        }
    }
}

二、快速排序

快速排序的思想很简单，就是先把待排序的数组拆成左右两个区间，左边都比中间的基准数小，右边都比基准数大。接着左右两边各自再做同样的操作，完成后再拆分再继续，一直到各区间只有一个数为止。

/**
 * 快速排序
 *
 * @param arr
 */
public void quickSort(int[] arr, int low, int high) {
    if (low >= high) {
        return;
    }
    int left = low;
    int right = high;
    int baseIndex = left;
    int base = arr[baseIndex];
    int tmp;
    while (left < right) {
        while (arr[right] >= base && left < right) {
            // 以base为基准，从右往左找到比基准小的数
            right--;
        }
        while (arr[left] <= base && left < right) {
            // 以base为基准，从左往右找到比基准大的数
            left++;
        }
        if (left < right) {
            // 左右还没相交，大小对换位置
            tmp = arr[left];
            arr[left] = arr[right];
            arr[right] = tmp;
        }
    }
    // 这一轮快排结束，交换相遇点与基准点，把基准数放在对应的位置上
    // 因为要把基准数和相遇点交换，由于if判断包含等于，那么从左往右就会找到比基准数小的数，从右往左就会找到比基准数大的数，会越过基准数
    // 因此当基准点小于相遇点时（基准点取第一位数），必须保证从先移动右指针，再移动左指针；当基准点大于相遇点时（基准点取最后一位位数），必须保证从先移动左指针，再移动右指针
    // 如果一定要随机基准数，有个简单的改进方法，就是随机一位数，与首位，或最后一位先做一下交换
    tmp = arr[baseIndex];
    arr[baseIndex] = arr[right];
    arr[right] = tmp;
    //数组“分两半”,再重复上面的操作
    quickSort(arr, low, left - 1);
    quickSort(arr, left + 1, high);
}

三、插入排序

插入排序是一种简单的排序方法，其基本思想是将一个记录插入到已经排好序的有序表中，使得被插入数的序列同样是有序的。按照此法对所有元素进行插入，直到整个序列排为有序的过程。

1. 直接插入排序

直接插入排序就是插入排序的粗暴实现。对于一个序列，选定一个下标，认为在这个下标之前的元素都是有序的。将下标所在的元素插入到其之前的序列中。接着再选取这个下标的后一个元素，继续重复操作。直到最后一个元素完成插入为止。我们一般从序列的第二个元素开始操作。

/**
 * 插入排序
 *
 * @param arr
 */
public void insertSort(int[] arr) {
    // 从第二个数开始遍历
    for (int i = 1; i < arr.length; i++) {
        // 插入的数
        int insertNum = arr[i];
        // 寻找插入点
        int insertIndex = 0;
        for (int j = 0; j < i; j++, insertIndex++) {
            // 插入点在比插入数大的这一位的前面
            if (insertNum < arr[j]) {
                break;
            }
        }
        // 从插入点往后依次挪动
        for (int j = i; j >= insertIndex; j--) {
            if (j > 0) {
                arr[j] = arr[j - 1];
            }
        }
        // 最后插入数据
        arr[insertIndex] = insertNum;
    }
}

插入排序对已经排好序的数组操作时，效率很高

2. 希尔排序

某些情况下直接插入排序的效率极低。比如一个已经有序的升序数组，这时再插入一个比最小值还要小的数，也就意味着被插入的数要和数组所有元素比较一次。我们需要对直接插入排序进行改进。

我们可以试着先将数组变为一个相对有序的数组，然后再做插入排序。

希尔排序的步骤简述如下：

1. 把元素按步长gap分组，gap的数值其实就是分组的个数。gap的起始值为数列长度的一半，每循环一轮gap减为原来的一半。
2. 对每组元素采用直接插入排序算法进行排序。
3. 随着步长逐渐减小，组就越少，组中包含的元素就越多。
4. 当步长值减小到1时，整个数据合成一组，最后再对这一组数列用直接插入排序进行最后的调整，最终完成排序。

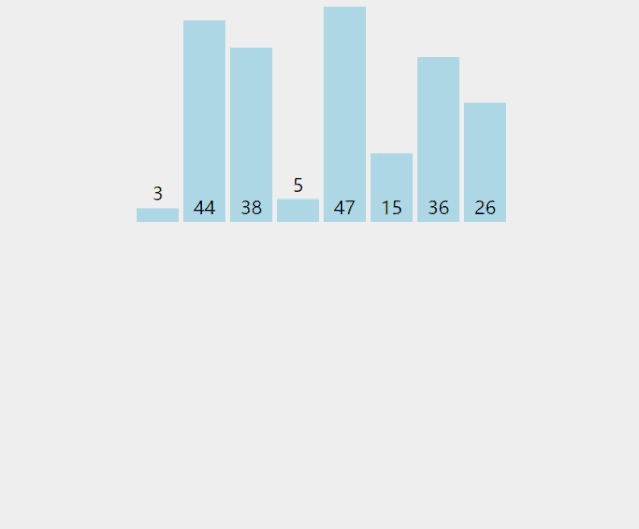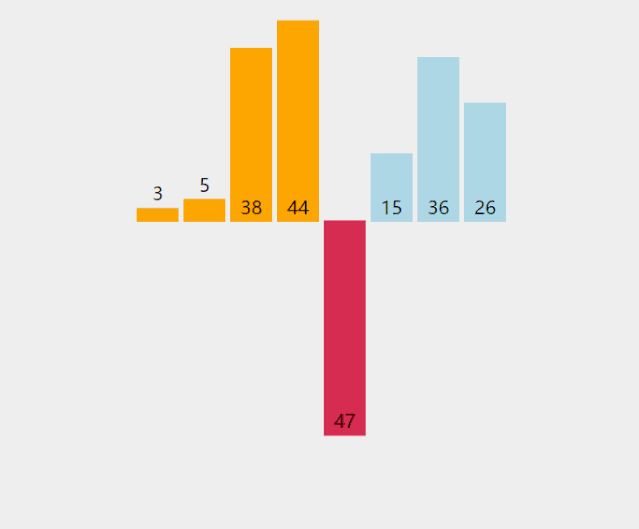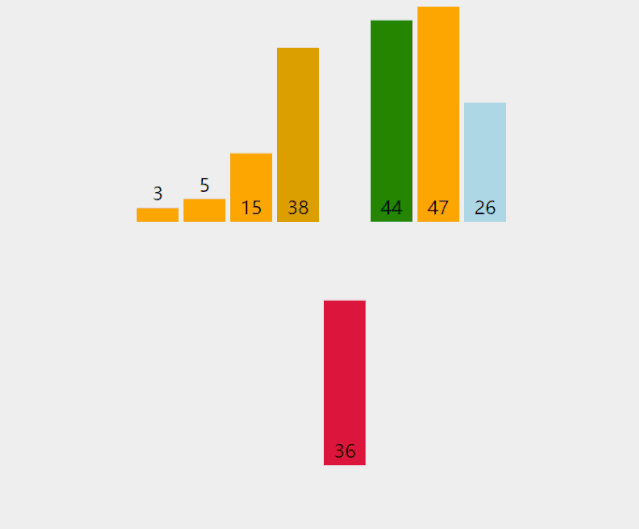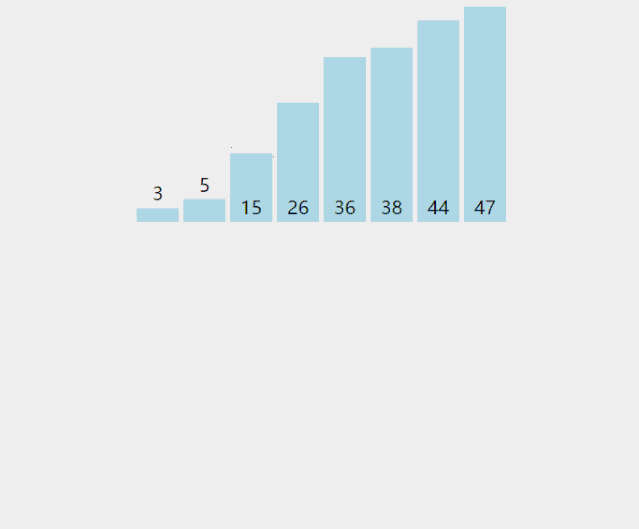
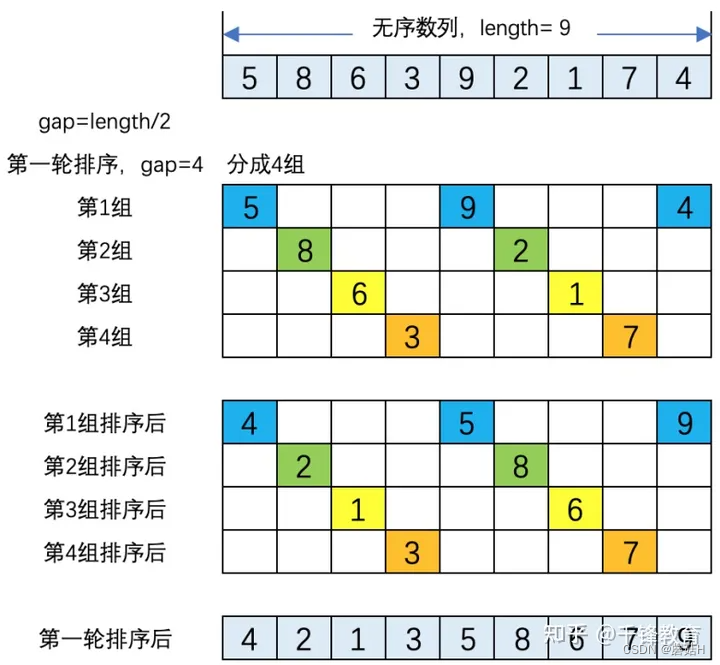
我们以无序数列[5，8，6，3，9，2，1，7，,4]为例，详细介绍希尔排序的步骤：

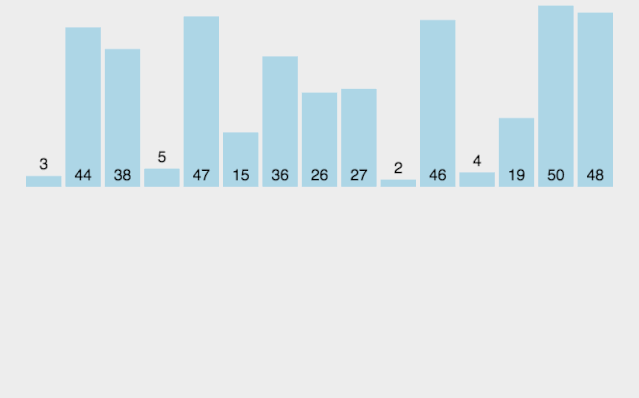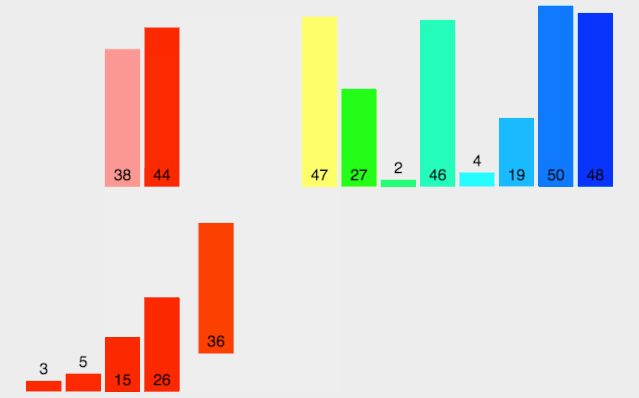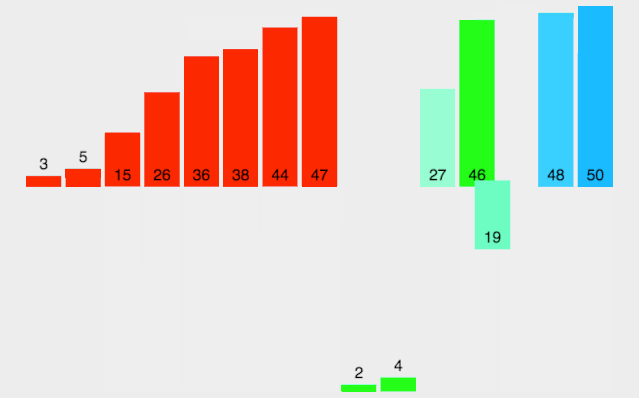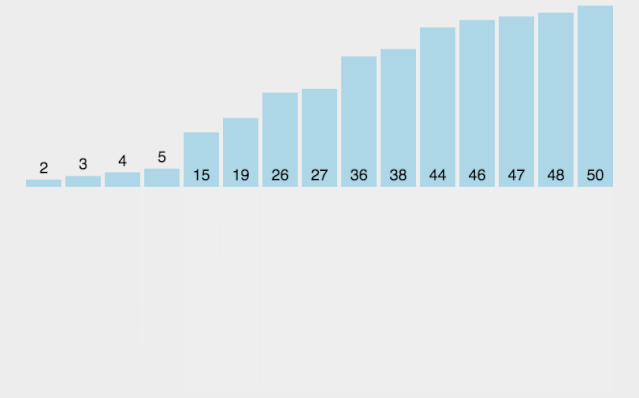
(1). 第一轮排序，gap = length/2 = 4，即将数组分成4组。四组元素分别为[5，9，4]、[8，2]、[6，1]、[3，,7]。对四组元素分别进行排序结果为：[4，5，9]、[2，8]、[1，6]、[3，7]。将四组排序结果进行合并，得到第一轮的排序结果为：[4，2，1，3，5，8，6，7，9]。如下图所示。

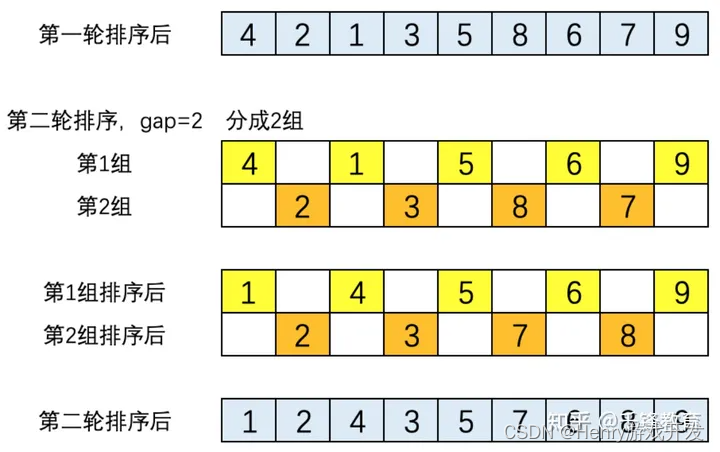
(2). 第二轮排序，gap = 2，将数列分成2组。两组的元素分别是[4，1，5，6，9]和[2，3，8，,7]。这两个组分别执行直接插入排序后的结果为[1，4，5，6，9]和[2，3，7，8]。将两组合并后的结果为[1，2，4，3，5，7，6，8，9]，如下图所示。

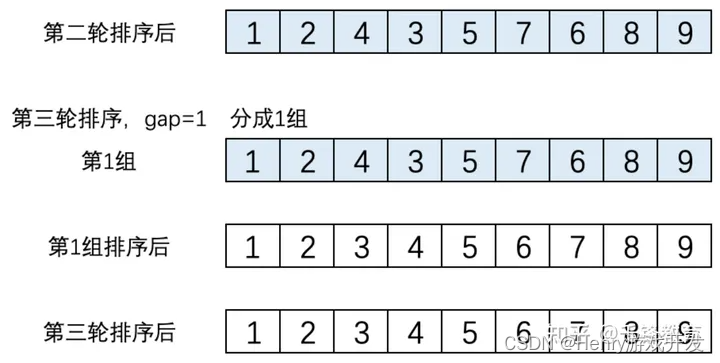
(3). 第三轮排序，gap = 1，数组就变成了一组。该组的元素是[1，2，4，3，5，7，6，8，9]，这个组执行直接插入排序后结果为[1，2，3，4，5，6，7，8，9]，这个结果就是第三轮排序后得到的结果。此时排序完成，如下图所示。

public void shellSort(int[] arr) {
    // gap 为步长，每次减为原来的一半。
    for (int gap = arr.length / 2; gap > 0; gap /= 2) {
        // 对每一组都执行直接插入排序
        for (int i = 0 ;i < gap; i++) {
            // 对本组数据执行直接插入排序
            for (int j = i + gap; j < arr.length; j += gap) {
                // 如果 a[j] < a[j-gap]，则寻找 a[j] 位置，并将后面数据的位置都后移
                if (arr[j] < arr[j - gap]) {
                    int k;
                    int temp = arr[j];
                    for (k = j - gap; k >= 0 && arr[k] > temp; k -= gap) {
                        arr[k + gap] = arr[k];
                    }
                    arr[k + gap] = temp;
                }
            }
        }
    }
}

四、选择排序

1. 简单选择排序

选择排序思想的暴力实现，每一趟从未排序的区间找到一个最小元素，并放到第一位，直到全部区间有序为止。

public void selectSort(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
        // 遍历数据
        int minIndex = i;
        for (int j = i + 1; j < arr.length; j++) {
            // 从当前位置往后遍历，找到最小数的下标
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }
        // 最小数的下标不是第一个数，那么就把最小下标和第一个数做交换
        if (i != minIndex) {
            int temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
        }
    }
}

2. 堆排序

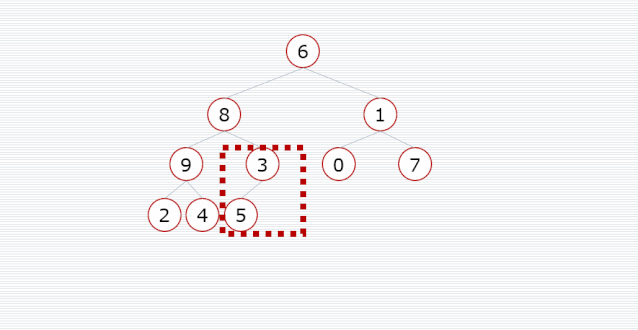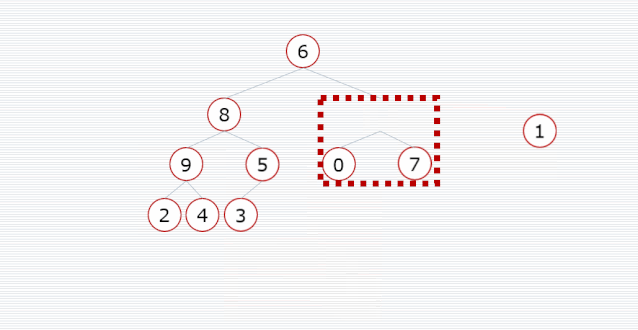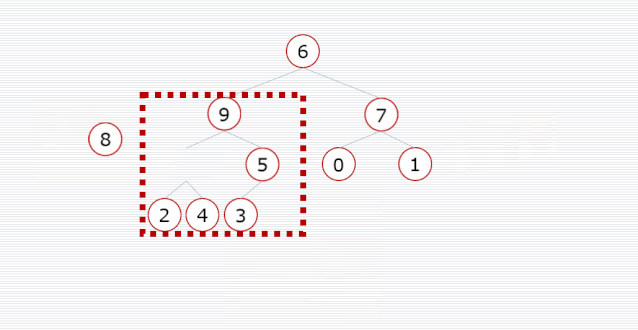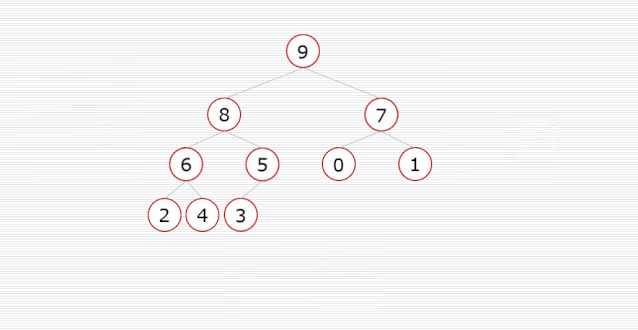
对于任何一个数组都可以看成一颗完全二叉树。堆是具有以下性质的完全二叉树

• 大顶堆：每个结点的值都大于或等于其左右孩子结点的值
• 小顶堆：每个结点的值都小于或等于其左右孩子结点的值
  

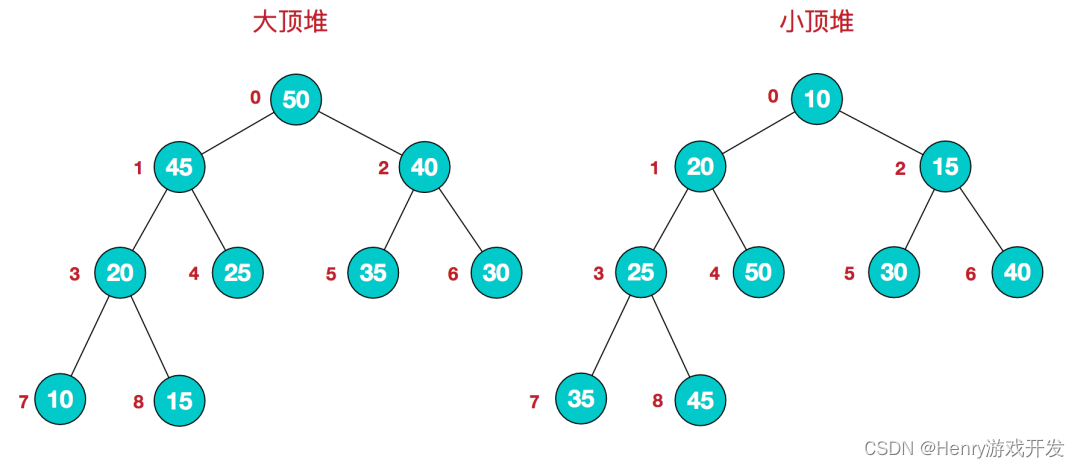
像上图的大顶堆，映射为数组，就是 [50, 45, 40, 20, 25, 35, 30, 10, 15]。可以发现第一个下标的元素就是最大值，将其与末尾元素交换，则末尾元素就是最大值。所以堆排序的思想可以归纳为以下两步：

1. 将待排序的数组初始化为大顶堆，该过程即建堆。
2. 将堆顶元素与最后一个元素进行交换，除去最后一个元素外可以组建为一个新的大顶堆。
3. 由于第二部堆顶元素跟最后一个元素交换后，新建立的堆不是大顶堆，需要重新建立大顶堆。重复上面的处理流程，直到堆中仅剩下一个元素。

重复以上两个步骤，直到没有元素可操作，就完成排序了。

我们需要把一个普通数组转换为大顶堆，调整的起始点是最后一个非叶子结点，然后从左至右，从下至上，继续调整其他非叶子结点，直到根结点为止。

/**
 * 堆排序
 *
 * @param arr
 */
public void heapSort(int[] arr) {
    // 开始位置是最后一个非叶子结点，即最后一个结点的父结点
    int start = (arr.length - 1) / 2;
    // 调整为大顶堆
    for (int i = start; i >= 0; i--) {
        maxHeap(arr, arr.length, i);
    }
    // 先把数组中第 0 个位置的数和堆中最后一个数交换位置，再把前面的处理为大顶堆
    for (int i = arr.length - 1; i > 0; i--) {
        int temp = arr[0];
        arr[0] = arr[i];
        arr[i] = temp;
        maxHeap(arr, i, 0);
    }
}
/**
 * 转化为大顶堆
 *
 * @param arr   待转化的数组
 * @param size  待调整的区间长度
 * @param index 结点下标
 */
public void maxHeap(int[] arr, int size, int index) {
    // 左子结点
    int leftNode = 2 * index + 1;
    // 右子结点
    int rightNode = 2 * index + 2;
    int max = index;
    // 和两个子结点分别对比，找出最大的结点
    if (leftNode < size && arr[leftNode] > arr[max]) {
        max = leftNode;
    }
    if (rightNode < size && arr[rightNode] > arr[max]) {
        max = rightNode;
    }
    // 交换位置
    if (max != index) {
        int temp = arr[index];
        arr[index] = arr[max];
        arr[max] = temp;
        // 因为交换位置后有可能使子树不满足大顶堆条件，所以要对子树进行调整
        maxHeap(arr, size, max);
    }
}

五、归并排序

归并排序是建立在归并操作上的一种有效，稳定的排序算法。该算法采用分治法的思想，是一个非常典型的应用。归并排序的思路如下：

1. 将 n 个元素分成两个各含 n/2 个元素的子序列
2. 借助递归，两个子序列分别继续进行第一步操作，直到不可再分为止
3. 此时每一层递归都有两个子序列，再将其合并，作为一个有序的子序列返回上一层，再继续合并，全部完成之后得到的就是一个有序的序列

关键在于两个子序列应该如何合并。假设两个子序列各自都是有序的，那么合并步骤就是：

1. 创建一个用于存放结果的临时数组，其长度是两个子序列合并后的长度
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置
3. 比较两个指针所指向的元素，选择相对小的元素放入临时数组，并移动指针到下一位置
4. 重复步骤 3 直到某一指针达到序列尾
5. 将另一序列剩下的所有元素直接复制到合并序列尾
   

/**
 * 合并数组
 */
public void merge(int[] arr, int low, int middle, int high) {
    // 用于存储归并后的临时数组
    int[] temp = new int[high - low + 1];
    // 记录第一个数组中需要遍历的下标
    int i = low;
    // 记录第二个数组中需要遍历的下标
    int j = middle + 1;
    // 记录在临时数组中存放的下标
    int index = 0;
    // 遍历两个数组，取出小的数字，放入临时数组中
    while (i <= middle && j <= high) {
        // 第一个数组的数据更小
        if (arr[i] <= arr[j]) {
            // 把更小的数据放入临时数组中
            temp[index] = arr[i];
            // 下标向后移动一位
            i++;
        } else {
            temp[index] = arr[j];
            j++;
        }
        index++;
    }
    // 处理剩余未比较的数据
    while (i <= middle) {
        temp[index] = arr[i];
        i++;
        index++;
    }
    while (j <= high) {
        temp[index] = arr[j];
        j++;
        index++;
    }
    // 把临时数组中的数据重新放入原数组
    for (int k = 0; k < temp.length; k++) {
        arr[k + low] = temp[k];
    }
}
/**
 * 归并排序
 */
public void mergeSort(int[] arr, int low, int high) {
    int middle = (high + low) / 2;
    if (low < high) {
        // 处理左边数组
        mergeSort(arr, low, middle);
        // 处理右边数组
        mergeSort(arr, middle + 1, high);
        // 归并
        merge(arr, low, middle, high);
    }
}

六、基数排序

基数排序的原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。为此需要将所有待比较的数值统一为同样的数位长度，数位不足的数在高位补零。

/**
 * 基数排序
 *
 * @param arr
 */
public void radixSort(int[] arr) {
    // 存放数组中的最大数字
    int max = Integer.MIN_VALUE;
    for (int value : arr) {
        if (value > max) {
            max = value;
        }
    }
    // 计算最大数字是几位数
    int maxLength = (max + "").length();
    // 用于临时存储数据（0-9）
    int[][] temp = new int[10][arr.length];
    // 用于记录在 temp 中相应的下标存放数字的数量（0-9）
    int[] counts = new int[10];
    // 根据最大长度的数决定比较次数（从低位往高位以此比较）
    for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {
        // 每一个数字分别计算余数
        for (int value : arr) {
            // 计算余数
            int remainder = value / n % 10;
            // 把当前遍历的数据放到指定的数组中
            temp[remainder][counts[remainder]] = value;
            // 记录数量
            counts[remainder]++;
        }
        // 记录取的元素需要放的位置
        int index = 0;
        // 把数字取出来
        for (int k = 0; k < counts.length; k++) {
            // 记录数量的数组中当前余数记录的数量不为 0
            if (counts[k] != 0) {
                // 循环取出元素
                for (int l = 0; l < counts[k]; l++) {
                    arr[index] = temp[k][l];
                    // 记录下一个位置
                    index++;
                }
                // 把数量置空
                counts[k] = 0;
            }
        }
    }
}

七、桶排序

桶排序（Bucket Sort）又称箱排序，是一种比较常用的排序算法。其算法原理是将数组分到有限数量的桶里，再对每个桶分别排好序（可以是递归使用桶排序，也可以是使用其他排序算法将每个桶分别排好序），最后一次将每个桶中排好序的数输出。

桶排序的思想就是把待排序的数尽量均匀地放到各个桶中，再对各个桶进行局部的排序，最后再按序将各个桶中的数输出，即可得到排好序的数。

1. 首先确定桶的个数。因为桶排序最好是将数据均匀地分散在各个桶中，那么桶的个数最好是应该根据数据的分散情况来确定。首先找出所有数据中的最大值mx和最小值mn；根据mx和mn确定每个桶所装的数据的范围 size，有size = (mx - mn) / n + 1，n为数据的个数，需要保证至少有一个桶，故而需要加个1；

求得了size即知道了每个桶所装数据的范围，还需要计算出所需的桶的个数cnt，有cnt = (mx - mn) / size + 1，需要保证每个桶至少要能装1个数，故而需要加个1；

2. 求得了size和cnt后，即可知第一个桶装的数据范围为 [mn, mn + size)，第二个桶为 [mn + size, mn + 2 * size)，…，以此类推因此步骤2中需要再扫描一遍数组，将待排序的各个数放进对应的桶中。
3. 对各个桶中的数据进行排序，可以使用其他的排序算法排序，例如快速排序；也可以递归使用桶排序进行排序；
4. 将各个桶中排好序的数据依次输出，最后得到的数据即为最终有序。

/**
 * 桶排序
 *
 * @param arr
 */
public void bucketSort(int[] arr) {
    int n = arr.length;
    int mn = arr[0], mx = arr[0];
    // 找出数组中的最大最小值
    for (int i = 1; i < n; i++) {
        mn = Math.min(mn, arr[i]);
        mx = Math.max(mx, arr[i]);
    }
    // 每个桶存储数的范围大小，使得数尽量均匀地分布在各个桶中，保证最少存储一个
    int size = (mx - mn) / n + 1;
    // 桶的个数，保证桶的个数至少为1
    int cnt = (mx - mn) / size + 1;
    // 声明cnt个桶
    List<Integer>[] buckets = new List[cnt];
    for (int i = 0; i < cnt; i++) {
        buckets[i] = new ArrayList<>();
    }
    // 扫描一遍数组，将数放进桶里
    for (int k : arr) {
        int idx = (k - mn) / size;
        buckets[idx].add(k);
    }
    // 对各个桶中的数进行排序，这里用库函数快速排序
    for (int i = 0; i < cnt; i++) {
        // 默认是按从小打到排序
        // 这里可以用任何的方式排序，这里直接用List的sort方法
        buckets[i].sort(null);
    }
    // 依次将各个桶中的数据放入返回数组中
    int index = 0;
    for (int i = 0; i < cnt; i++) {
        for (int j = 0; j < buckets[i].size(); j++) {
            arr[index++] = buckets[i].get(j);
        }
    }
}

排序算法对比

排序算法	时间复杂度(平均)	时间复杂度(最坏)	时间复杂度(最好)	空间复杂度	稳定性
冒泡排序	O(n2)	O(n2)	O(n)	O(1)	稳定
选择排序	O(n2)	O(n2)	O(n2)	O(1)	不稳定
插入排序	O(n2)	O(n2)	O(n)	O(1)	稳定
快速排序	O(nlogn)	O(n2)	O(nlogn)	O(nlogn)	不稳定
堆排序	O(nlogn)	O(nlogn)	O(nlogn)	O(1)	不稳定
希尔排序	O(n^1.3)	O(n2)	O(n)	O(1)	不稳定
归并排序	O(nlogn)	O(nlogn)	O(nlogn)	O(n)	稳定
基数排序	O(d(n+k))	O(d(n+k))	O(d(n+k))	O(n+k)	稳定
桶排序	O(n+k)	O(n2)	O(n)	O(n+k)	稳定

参考资料：https://mp.weixin.qq.com/s?__biz=MzAxMjY5NDU2Ng==&mid=2651862169&idx=1&sn=e011e79ff77736dfb389084bb3a20d37&chksm=804971d0b73ef8c649d7c9b08706f3c33b0e10c3935e24982337b05d69f1487ace072fbd48d9&scene=27