超详细解释密码学中六种攻击模型

目录

一. 前言

二. 唯密文攻击（ciphertext-only attack）

三. 已知明文攻击（known plaintext attack）

四. 选择性明文攻击（chosen plaintext attack，CPA）

五. 选择性密文攻击（chosen ciphertext attack，CCA）

六.?自适应选择明文攻击 (adaptive-chosen- plaintext attack)

七.?选择密钥攻击(Chosen- key attack)

八. 攻击的具体方法

8.1 穷举攻击

8.2? 统计分析攻击

8.3 数学分析攻击

---

一. 前言

敌手的攻击模型又被叫做威胁模型（threat models），在密码学中通常有六种：唯密文攻击，已知明文攻击，选择性明文攻击，选择性密文攻击，自适应选择性密文攻击，自适应选择性明文攻击，选择密钥攻击。

二. 唯密文攻击（ciphertext-only attack）

已知：敌手仅能看到密文

目标：推导这些密文对应的明文

经典密码学使用的攻击模型大都是唯密文攻击（比如维吉尼亚密码）。敌手有消息的密文，这些消息都用同一算法加密。敌手的任务是恢复出明文，或者最好是能推算出密钥来，以便可采用相同的密钥解出其他被加密的消息。因为敌手所能利用的数据资源仅为密文，因此这是对密码分析者最不利的情况。写成密码学的标准格式：

三. 已知明文攻击（known plaintext attack）

已知：敌手能看到一些明文对应的密文，注意这些明文/密文对是由挑战者选取的。

目标：给出新的密文，尝试推导其明文

传统的经典密码学在此攻击模型下都不安全。敌手不仅可得到一些密文，而且也知道这些密文对应的明文。敌手的任务推导出密钥或导出一个算法，此算法可以对任何新的密文进行解密。

例如，敌手可能知道从用户终端送到计算机的密文数据从一个标准词“LOGIN”开头。

又例如，加密成密文的计算机程序文件特别容易受到这种攻击。这是因为诸如“BEGIN”，“END”，“IF”，“THEN”，“ELSE”等词的密文有规律地在密文中出现。

写成密码学的格式如下：

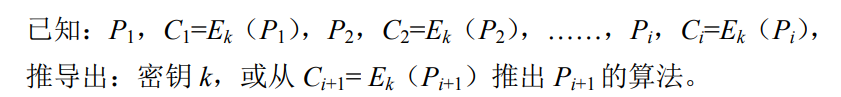
四. 选择性明文攻击（chosen plaintext attack，CPA）

已知：敌手能看到一些明文对应的密文，注意这些明文/密文对是由敌手选取的。

目标：给出新的密文，尝试推导其明文

备注：密码分析者，密码攻击者，敌手，这三者一般我们认为是一样的。

敌手不仅可得到一些密文和相应的明文，而且他们也可选择被加密的明文。这比已知明文攻击更有效。因为敌手能选择特定的明文块去加密，那些块可能产生更多关于密钥的信息。这是对密码分析者十分有利的情况。分析者的任务是推出用密钥或导出一个算法，此算法可以对任何新的密文进行解密。

如果分析员能够设法在源系统插入由该分析员选择的消息，则可进行选择明文攻击。

一般而言，如果分析员能够选择消息来加密，那么他可能故意选择能够揭露出密钥结构的模式。计算机文件系统和数据库系统特别容易受到这种攻击，因为用户可以随意选择明文，并获得相应的密文数据库。

五. 选择性密文攻击（chosen ciphertext attack，CCA）

已知：敌手可以任意选择密文，来观察解密出的明文。不仅如此，敌手还可以选择解密无意义的密文，来获取更多信息。

目标：给出新的密文，尝试从密文中获取关于明文的信息（哪怕一部分也可以）

所谓选择密文攻击是指密码分析者能够选择不同的密文，并获得相应的明文。例如密码分析者存取一个防窜改的自动解密盒，密码分析者的任务是推导出密钥。

六.?自适应选择明文攻击 (adaptive chosen plaintext attack)

这是选择明文攻击的特殊情况。

密码分析者不仅能选择被加密的明文，而且也能基于以前加密的结果修正这个选择。在选择明文攻击中，密码分析者还可以选择一大块被加了密的明文。

而在自适应选择密文攻击中，他可选取较小的明文块，然后再基于第一块的结果选择另一明文块，以此类推。

七.?选择密钥攻击(Chosen key attack)

这种攻击并不表示密码分析者能够选择密钥，它只表示密码分析者知道不同密钥之间的关系。

八. 攻击的具体方法

密码学对安全性的假设都要求，对密码进行分析的尝试称为攻击。Kerckhoffs 最早在 19 世纪阐明密码分析的一个基本假设，这个假设就是秘密必须完全藏在密钥中。Kerckhoffs假设攻击者已有密码算法及其实现的全部详细资料。

攻击密码系统的方法主要有以下三种。

8.1 穷举攻击

所谓穷举攻击是指密码分析者采用：

1. 依次试遍所有可能的密钥来解密文，直至得到正确的明文；
2. 或者用一个确定的密钥对所有可能的明文进行加密，直至得到所获得的密文。

显然，理论上对于任何实用密码只要有足够的资源，都可以用穷举攻击将其攻破。 穷举攻击所花费的时间等于尝试次数乘以一次解密(加密)所需的时间。显然可以通过增大密钥量或加大解密(加密)算法的复杂性来对抗穷举攻击。当密钥量增大时，尝试的次数必然增大。当解密(加密)算法的复杂性增大时，完成一次解密(加密)所需的时间增大。从而使穷举攻击在实际上不能实现。穷举攻击是对密码的一种最基本的攻击。

8.2? 统计分析攻击

所谓统计分析攻击就是指密码分析者通过分析密文和明文的统计规律来破译密码。统计分析攻击在历史上为破译密码作出过极大的贡献。许多古典密码都可以通过分析密文字母和字母组的频率和其他统计参数而破译。对抗统计分析攻击的方法是设法使明文的统计特性不带入密文。这样，密文不带有明文的痕迹，从而使统计分析攻击成为不可能。能够抵抗统计分析攻击已成为近代密码的基本要求。

8.3 数学分析攻击

所谓数学分析攻击是指密码分析者针对加解密算法的数学基础和某些密码学特性，通过数学求解的方法来破译密码。数学分析攻击是对基于数学难题的各种密码的主要威胁。为了对抗这种数学分析攻击，应当选用具有坚实数学基础和足够复杂的加解密算法。