力扣（144. 二叉树的前序遍历&&94.二叉树的中序遍历&&145. 二叉树的后序遍历）

题目链接

题目1：

思路：较简单的思路，就是先将左孩子全部入栈，然后出栈访问右孩子，右孩子为空，再出栈，不为空，右孩子入栈，然后再次循环访问左孩子。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> v;
        if(root == nullptr)
            return v;
        TreeNode* cur = root;
        stack<TreeNode*> st;
        while(cur || !st.empty())
        {
            //左孩子全部入栈
            while(cur)
            {
                v.push_back(cur->val); //入栈同时访问
                st.push(cur);
                cur = cur->left;
            }
            cur = st.top();//开始访问栈里面的右孩子   
            st.pop();   
            cur = cur->right;
        }
        return v;
    }
};

题目链接
题目2：

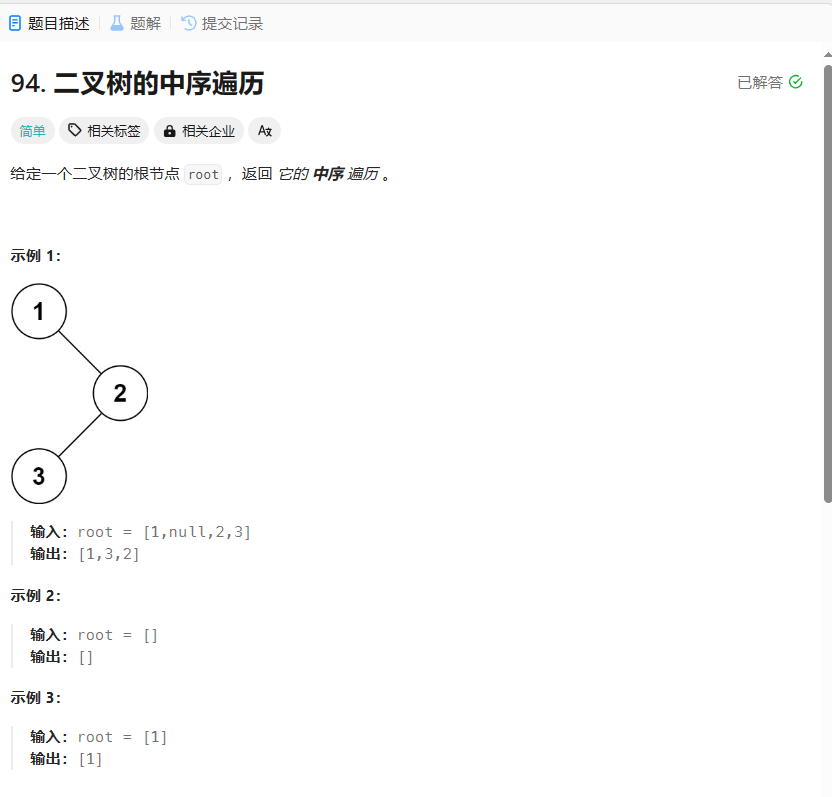
思路：同前序遍历一样，只不过访问结点，改为出栈时访问。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        //1.结点的左孩子先入栈
        //2.入完了之后，出栈访问，在访问右子树
        //3.重复2，3 直到栈为空
        stack<TreeNode*> st;
        vector<int> v;
        if(root == nullptr)
        {
            return v;
        }

        TreeNode* cur = root;
        while(cur || !st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }
            
            cur = st.top();  //出栈访问
            v.push_back(cur->val);
            st.pop();
            
            cur = cur->right;
        }
        return v;

    }
};

题目3链接
题目3：

思路1：同样跟前面两种方法类似。首先保证左子树全部入栈。区别不同的是，后序遍历，是要经过两次根结点的，那么什么时候访问呢？获取栈顶元素，然后看该结点的右孩子是否为空，或者右孩子是不是已经访问过。否则就继续将右子树入栈。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        
        vector<int> v;
        if(root==nullptr)
        {
            return v;
        }
        TreeNode * cur = root;
        stack<TreeNode*> st;
        TreeNode* prev = nullptr;
        while(cur || !st.empty())
        {
            //左路结点入栈
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }
            
            TreeNode* top = st.top();  //记录左路结点，左路节点的左子树已经访问完了
            //1.右为空，直接访问该结点。右为空，右子树已经访问完了，可以访问该结点了。
            if(top->right == nullptr || top->right == prev)
            {
                v.push_back(top->val);
                st.pop();
                prev = top;
            }
            else
            {
                cur = top->right;   //访问左路节点的右子树  -- 子问题
            }
        }
        return v;
    }
};

思路2：先序遍历是根左右。后序遍历是左右根。
那么先序遍历成根右左，再转换就是左右根。（这就转换成了后序遍历的结果了）