算法基础之整数划分

整数划分

• 核心思想： 计数类dp

背包做法

• f[i][j] 表示 取 1 – i 的物品 总容量为j的选法数量

  • f[i][j] = f[i-1][j] + f[i-1][j-v[i]] +f[i-1][j-2v[i]] +f[i-1][j-3v[i]] +……+f[i-1][j-kv[i]]

  • f[i][j-v[i]] = f[i-1][j-v[i]] +f[i-1][j-2v[i]] +f[i-1][j-3v[i]] +……+f[i-1][j-kv[i]]

    • f[i][j] = f[i-1][j] + f[i][j-v[i]]; (本题中 v[i] = i)

    • 

    •   #include<iostream>
        #include<cstring>
        #include<algorithm>
        
        using namespace std;
        const int N = 1010 , mod = 1e9 + 7;;
        
        int n;
        int f[N];
        
        int main()
        {
            cin>>n;
            
            f[0] = 1;  //f[0] 没有数 方法是1种
            for(int i=1;i<=n;i++)
                for(int j=i;j<=n;j++)
                    //f[i][j - i] = f[i][j - i] + f[i][j - 2] + ... + f[i][j - k]
                    //f[j-i] 
                    f[j] = (f[j] + f[j - i]) % mod;
                    
            cout<<f[n];
        }
      

dp做法

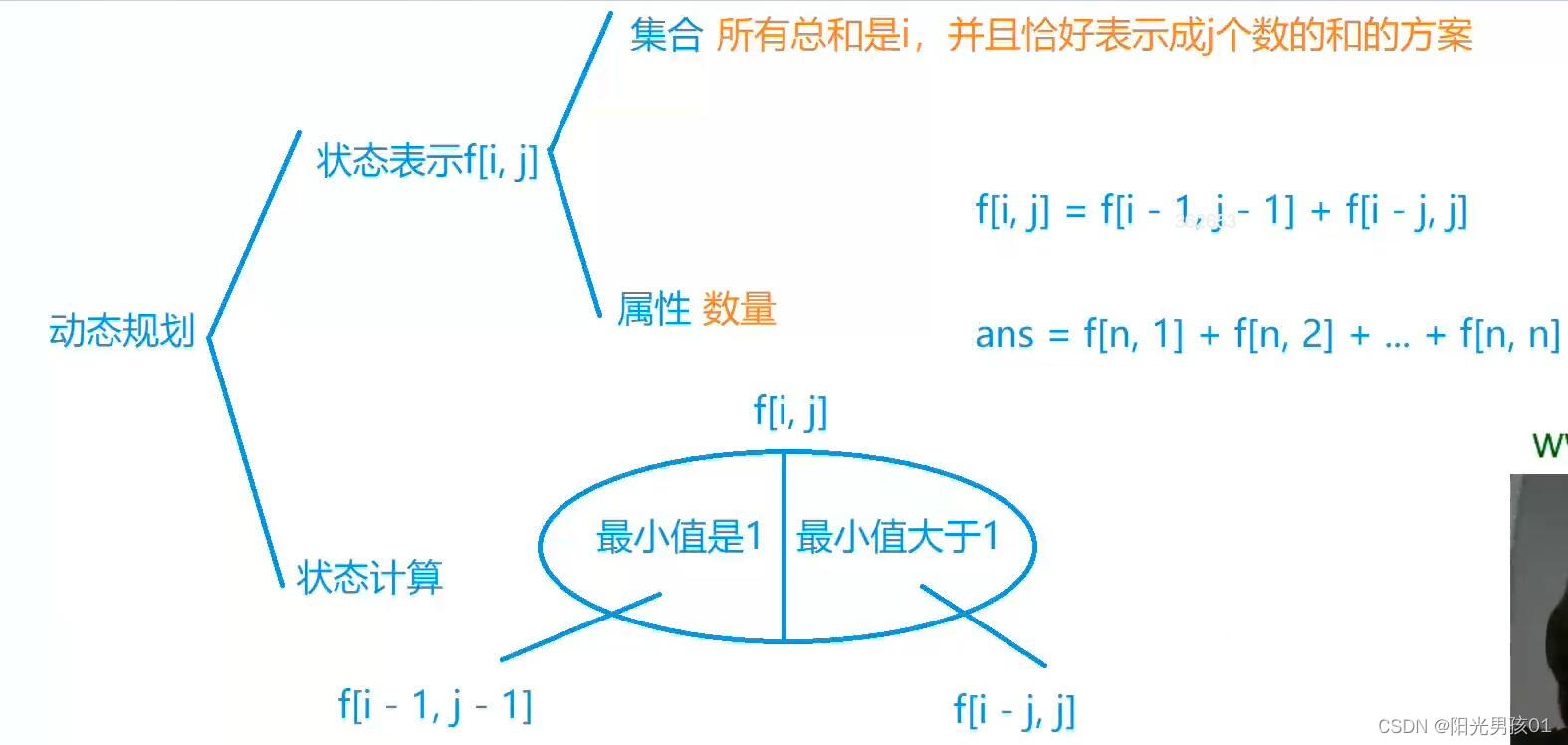
• f[i][j] 表示总和为i 总共j个数的方案数量

  • 将f[i][j] 分为 最小值是1的方案 和 最小值大于1的方案 两部分 (不重不漏)

    • 最小值是1: 在集合中–1 –> f[i-1][j-1] 总和为i-1 个数为j-1
    • 最小值大于1 : 将集合总每个数-1 –> f[i-j][j] 总和为i-j 个数为j

  • 则f[i][j] = f[i-1][j-1] + f[i-j][j]

    • 

  • 结果 : res = f[n][1] + f[n][2] +f[n][3] + … + f[n][n] (1个数的方案+2个数的方案+ … +n个数的方案)

    •   #include<iostream>
        #include<cstring>
        #include<algorithm>
        
        using namespace std;
        const int N = 1010 , mod = 1e9 + 7;;
        
        int n;
        int f[N][N];
        
        int main()
        {
            cin>>n;
            
            f[0][0] = 1;
            for(int i=1;i<=n;i++)
            {
                for(int j=1;j<=i;j++)  //总和为i 个数最多为i
                {
                    f[i][j] = (f[i-1][j-1] + f[i - j][j] ) % mod;    
                }
            }
            
            int res = 0;
            for(int i=1;i<=n;i++) res = (res + f[n][i]) % mod;
            
            cout<<res;
        }