数据结构实验报告-排序、查找及其应用

数据结构实验报告-排序、查找及其应用

一、问题分析

（1）题目一中，要求在坐标系中设立邮局，使得各个居民到邮局路程的和最小。题目中比较关键的信息时居民走到邮局是走平行于坐标轴的路径，不是直线路径。因为路径与坐标轴平行，所以x轴和y轴是可以独立分析的。这样，只要居民的位置确定了，它的横坐标与纵坐标的对应关系并不用关心，只要分别求出在两个坐标轴上各点到邮局在该坐标轴上投影的点的最小距离，两个局部最小之和即是全局最小。因为要求出各点到投影点的最小距离，一个按升序排列的点坐标可以在只遍历一次所有居民位置的情况下，按照递推公式以O(n)的时间复杂度得到最小距离。所以还要对居民的横坐标和纵坐标分别进行排序。因为数据的无序性，采用平均时间复杂度的O(nlog2n)的快速排序即可。
（2）题目二中，邮递员的年龄范围很小，限定在18到65岁，并且要求时间和空间复杂度都为O(n)。对于这种比较小的数据范围，采用桶排序是很适合的。每个年龄对应一个桶，因为题目不需要知道每个年龄有多少人，只要在那个年龄有邮递员，就将这个桶标记为1即可。读入所有数据后，从18遍历到65，只要有值，就拿它与上一个有值的年龄相减，维护一个最大值就可以得到答案。
（3）题目三中，邮递员和街道的关系是多对一，但是一个邮递员只负责一个街道。现在需要根据部分邮递员的回答来计算最小可能的邮递员总数。分析可以知道，不同回答的邮递员一定不会负责同一条街道，相同回答的邮递员可以假设他们负责同一条街道。这样，可以把相同回答的邮递员尽可能分到相同条街道，当分配不够时，就得从没有回答问题的邮递员中加人来负责该街道。根据这个策略，可以先排序，这样相同回答的邮递员位置就会相邻，只需以O(n)时间复杂度遍历一遍回答的数组，就可以得到最后的答案。
三个题目都是依赖排序后数据排序连续的良好性质，在这个基础上进行相应的逻辑操作，减小后面操作的时间和空间复杂度。

二、详细设计

2.1设计思想

（1）题目一需要使用到排序算法。这里采用比较快的快速排序，分别对每个居民的横坐标和纵坐标进行排序，可以得到在x轴和y轴上从小到大的n个点。然后分别遍历两个坐标轴。以遍历x轴为例，先计算其上所有点到其上数值最小（最左边）的点的距离，然后就可以带入递推公式来计算其他点的距离。对于一点(a,0),所有点到(a-1,0)的距离d已经求出，则所有点到(a,0)的距离等于d加上a左边所有点的数量，再减去a-1右边所有点的数量。因为从(a-1,0)转移到(a,0)，(a,0)左边每个点到(a,0)的距离相比于(a-1,0)时要增一，而对于(a-1,0)右边的点要减一，这两个因素共同作用的效果可以得到上述递推公式。两个坐标轴都维护一个最小值，他们对应坐标的交叉点就是邮局的最优地点。因为题目只要求求出最小值即可，最优坐标的信息可以不保留。最后将两个最小值相加就是所求答案。
（2）题目二采用桶排序。先设置一个大小为100的桶，实际上只用到18-65这个区间的桶即可。每读入一个年龄，就将该年龄对应的桶值置为1，表示该年龄有邮递员。读入完后，遍历桶中18到65的值，并用一个变量来保留上一个有值的桶下标（即相邻的年龄），如果有值就拿他的年龄与相邻年龄相减，维护这个差值的最大值就可以了。
（3）题目三先将所有回答进行快速排序，使相同回答的邮递员紧挨在一起。然后先将邮递员的初始数量置为已经回答的邮递员数量，然后开始对相同回答的邮递员配对分组。用一个变量sameAns记录上一个邮递员回答的值，一个变量sameCount记录目前有多少个邮递员分配到同一个街道。如果sameCount值等于sameAns时，说明可以配成一组，将sameCount的值置为-1，这个值是根据我的实现方式决定的，其实就是一个初始值；而如果在sameAns即将发生改变时，如果sameCount没有达到sameAns，即在已回答的邮递员中凑不成一组，则剩下的人需要在未回答的邮递员中补齐。这样遍历一遍回答的数组就可以得到最小可能的邮递员数量了。

2.2 存储结构及操作

2.2.1存储结构
实验中的数据存储都使用了基于线性存储的数组。
题目一中使用了int类型的数组x和y，分别记录每个居民的位置坐标。
题目二中使用了int类型的数组bucket，作为桶排序中的桶记录年龄。
题目三种使用了int类型的数组array，记录每位邮递员的回答。
2.2.2 涉及的操作
整个实验中用到的关键函数，如表 1所示。

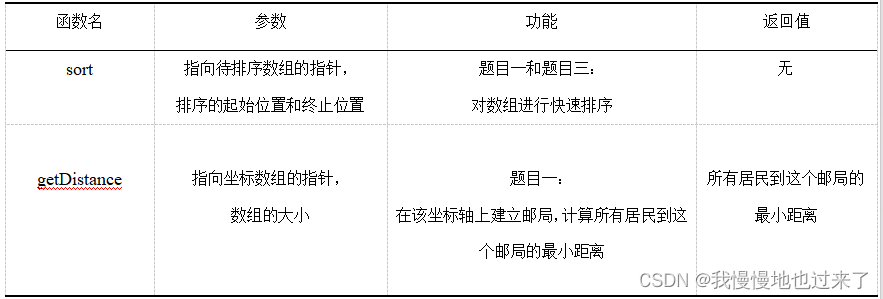
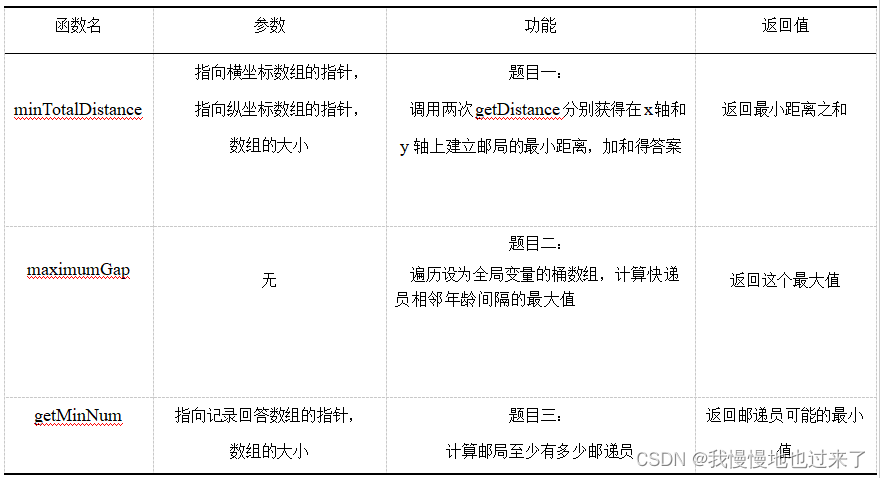
表 1（续表）

2.3 程序整体流程

（1）题目二中的流程图如图 1所示。

图 1
（2）快速排序的流程图如图 2所示。

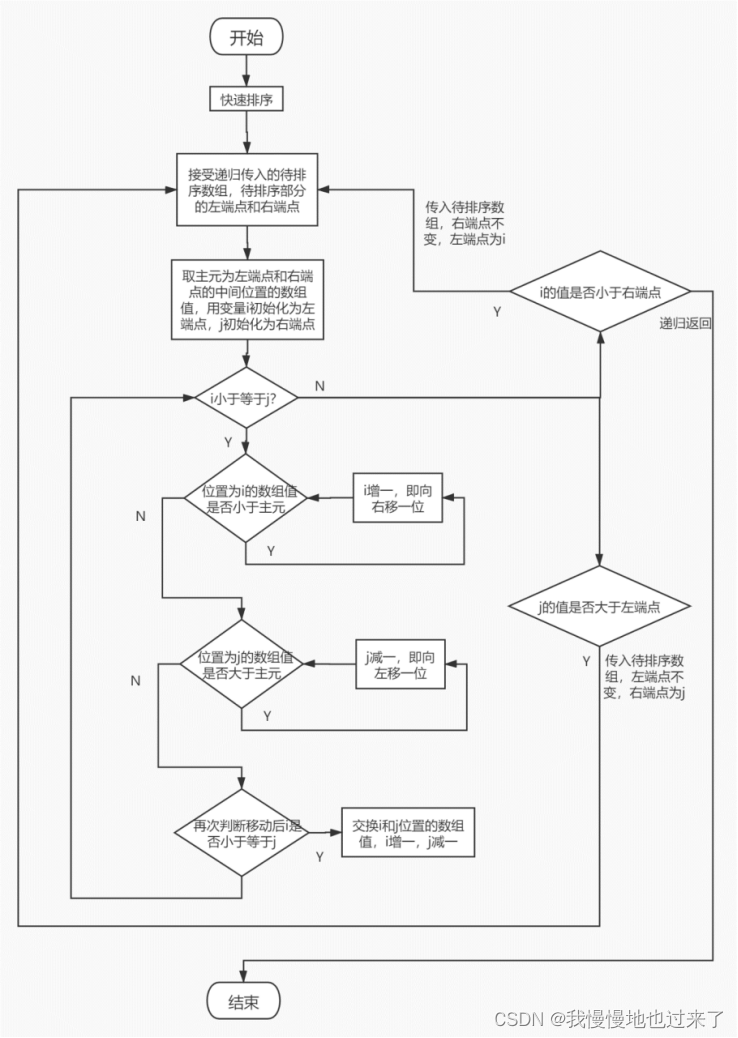
图 2
（2）题目一的流程图如图 3所示。

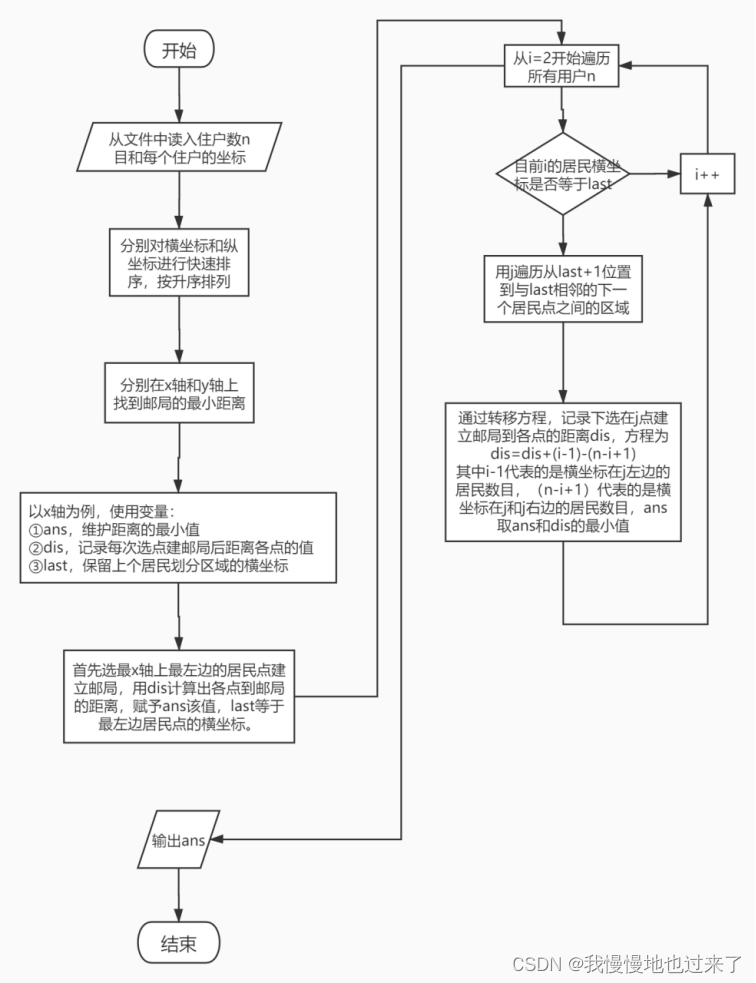
图 3

（3）题目三的整体流程和具体算法，如图 4所示。

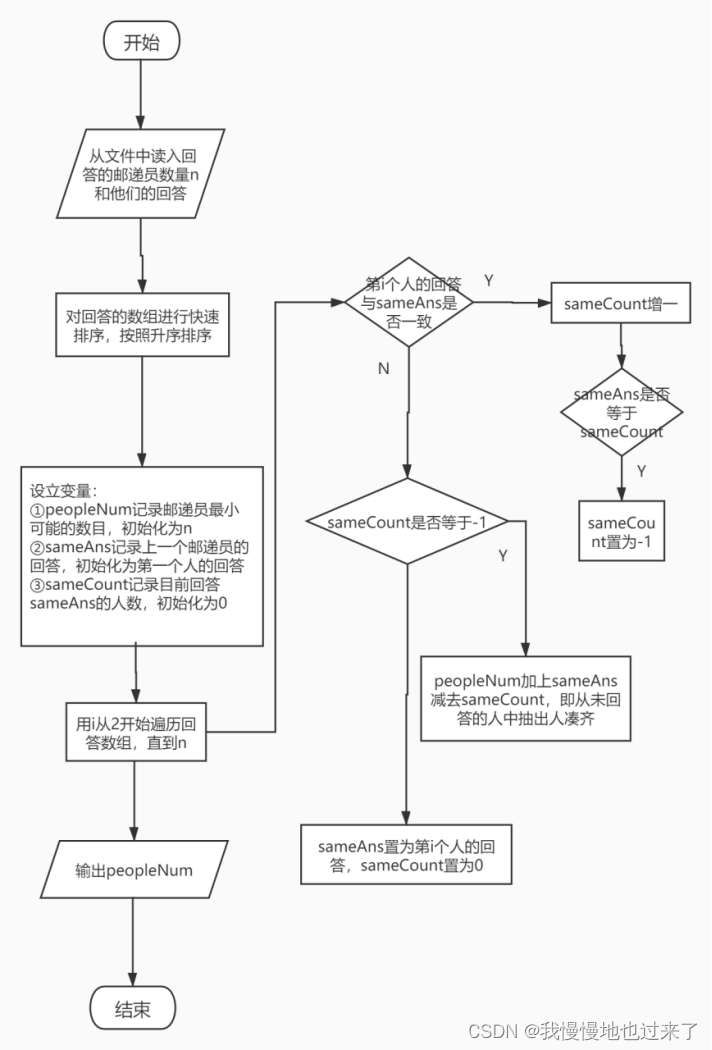
图 4

三、用户手册

程序分为题目一，题目二和题目三，均采用从文件中读取数据的方式读入，并含有多组数据的读入。在程序运行后无需其他操作就可得到结果。
（1）题目一中，将会读取文件名为“5_1_input.in”的文件中数据，此文件要放置在.c文件的同一目录下。每组数据第一行为住户数目n，第2行到第n+1行为每个住户的横坐标和纵坐标。
对于每一组输入，程序都会输出分隔符：
======Case ======
另起一行输出一个整数，代表建立每个居民到邮局距离之和的最小值。
（2）题目二中，将会读取文件名为“5_2_input.in”的文件中数据，此文件要放置在.c文件的同一目录下。每组数据第一行为邮递员总数n，第2行有n个数，代表每一个邮递员的年龄。
对于每一组输入，程序都会输出分隔符：
======Case ======
另起一行输出一个整数，代表相邻年龄间隔的最大值。
（3）题目三中，将会读取文件名为“5_3_input.in”的文件中数据，此文件要放置在.c文件的同一目录下。每组数据第一行为参与回答的邮递员数目n，第2行有n个数，代表一个回答，即有多少个邮递员和他负责同一条街道。
对于每一组输入，程序都会输出分隔符：
======Case ======
另起一行输出一个整数，代表邮局最少的邮递员数目。

四、结果

结果只给出程序输出截图，文件部分的输入数据已打包进压缩包。

（1）题目一输出截图如图 5所示。

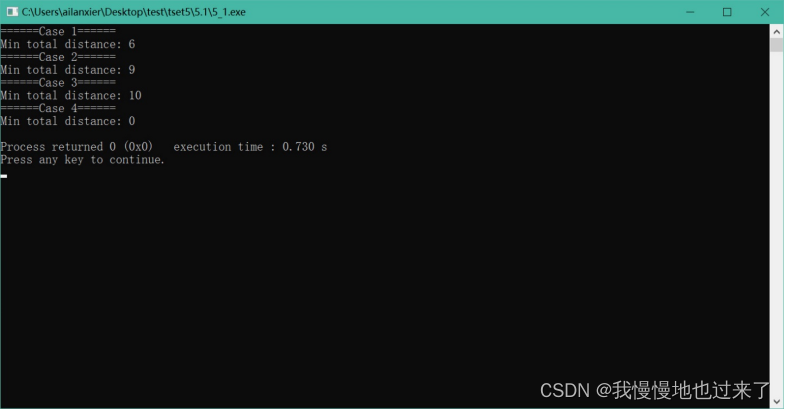
图 5

（2）题目二输出截图如图 6所示。

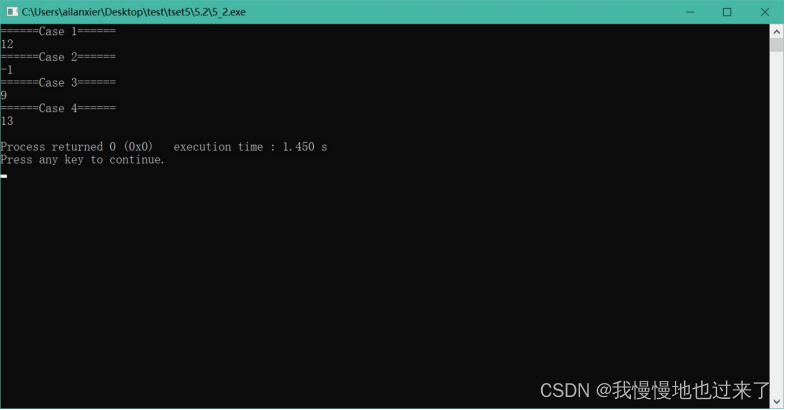
图 6

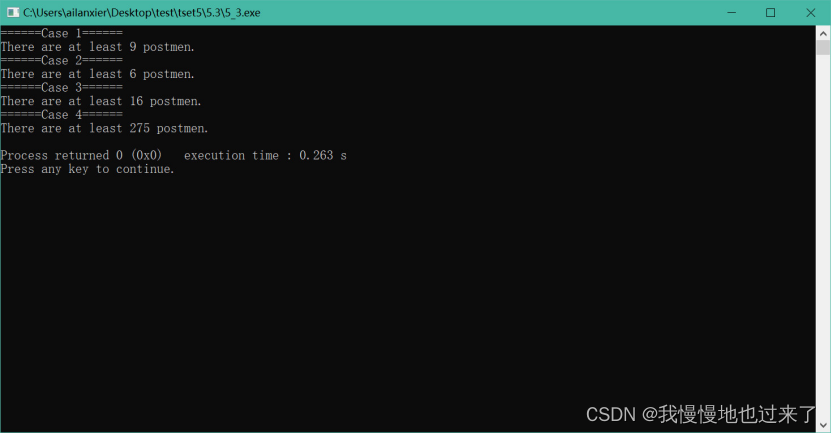
（3）题目三的截图如图 7所示。

图 7

五、总结

本次实验主要考察排序算法及其应用，对查找的要求不高。题目一和题目三主要采取快速排序对给出的完全随机无序的数据进行排序，题目二中根据题目要求以O(n)的时间复杂度解决问题且数据范围小，采用桶排序进行排序。排序在题目中是作为一个解决问题的工具，实验的主要逻辑是基于已有序的数据来完成的。题目一中需要根据题目给出的曼哈顿距离，判断出在x轴和y轴上分析问题时独立的，互不干扰。题目二在桶排序后，相邻年龄的邮递员在桶数组中位置也是相邻的，维护一个间隔最大值即可。题目三则是尽可能让相同回答的邮递员凑成一组，实在凑不成才从未回答的邮递员中加人。如果没有排序的预处理，后面处理问题的复杂度就会高出很多。
实验中我学会了使用时间复杂度O(nlog2n)的快速排序，也掌握了比较基础的时间和空间复杂度为O(n)的桶排序。解决问题时并没有运用特定的算法，而且在分析问题后，根据最优的策略来模拟，维护出最大值或者最小值就可以了。所以具体问题要具体分析，不能随便套模板就可以了。
实验中也遇到了不少难点。比如题目一对我来说还是比较难的，在课上完成时并没有想到x轴和y轴可以独立分析这一良好性质，而是采用时间和空间复杂度均为O(n2)的实现方法。在课后仔细思考时才有了突破点。所以解决问题的方法很多，如果多方面思考，有时可以很大程度地降低时间和空间复杂度。相信通过这一学期数据结构的学习，对以后掌握更多算法，培养计算机思维有很大帮助。