【数据结构与算法】quicksort快速排序算法大全：快速排序hoare法，快速排序挖坑法，快速排序前后指针法，快速排序优化，快速排序的非递归实现

一、快速排序算法

快速排序使用分治的思想来进行排序，其基本过程如下：

1. 从待排序数组中选择一个元素作为枢轴（pivot）。
2. 将数组分割成两个子数组，使得左侧子数组的元素都小于等于枢轴，右侧子数组的元素都大于等于枢轴。这个分割的过程称为划分（partition）。
3. 对左右子数组分别递归地进行快速排序。
4. 递归结束的条件是子数组只有一个元素或者为空。

时空复杂度：?

• 平均时间复杂度：O(nlogn)
• 当数组有序时，最坏时间复杂度：O(n^2)
• 空间复杂度：O(logn)

1、hoare划分法

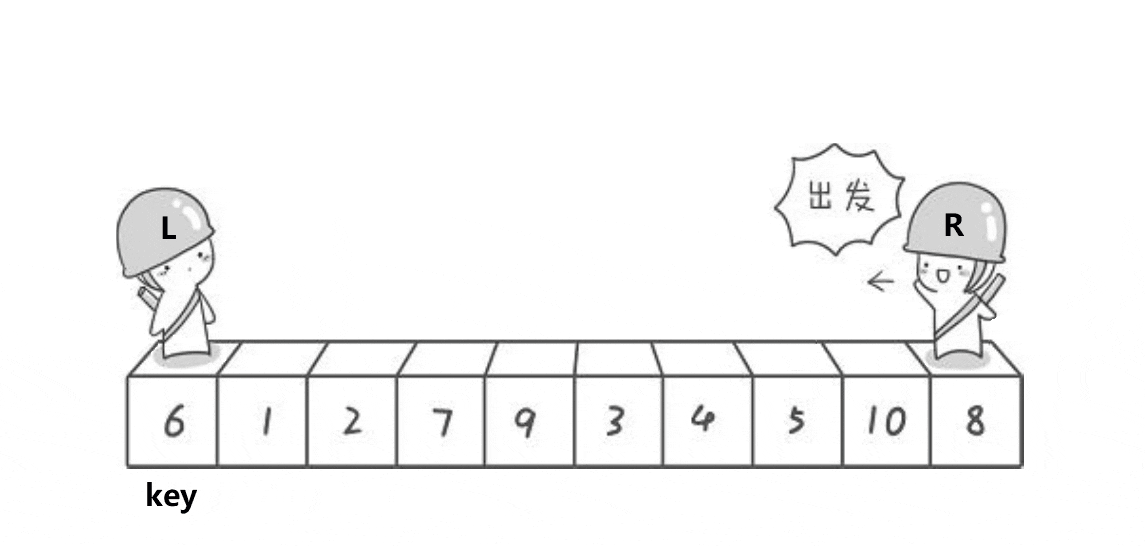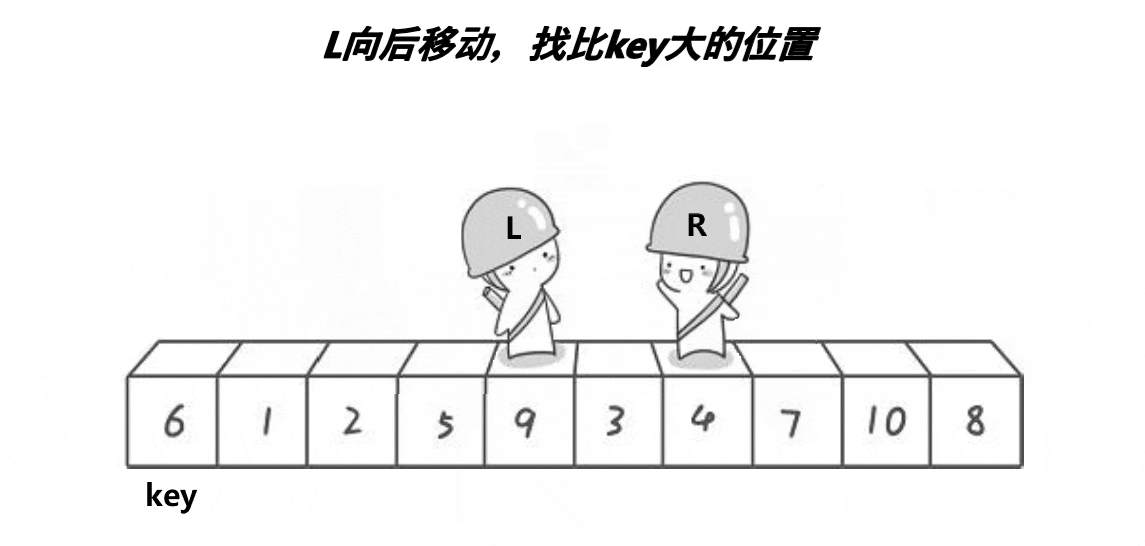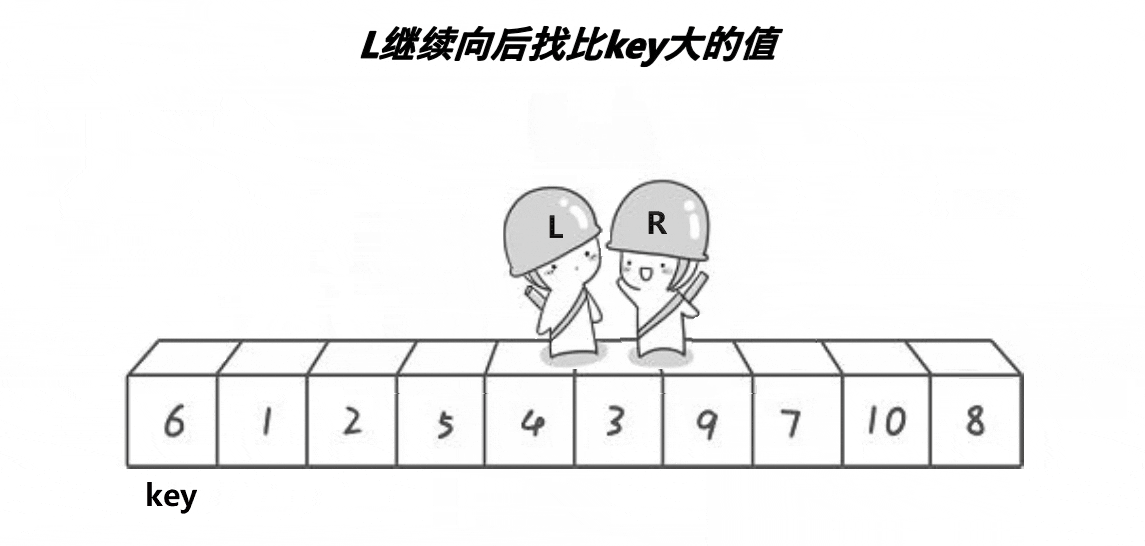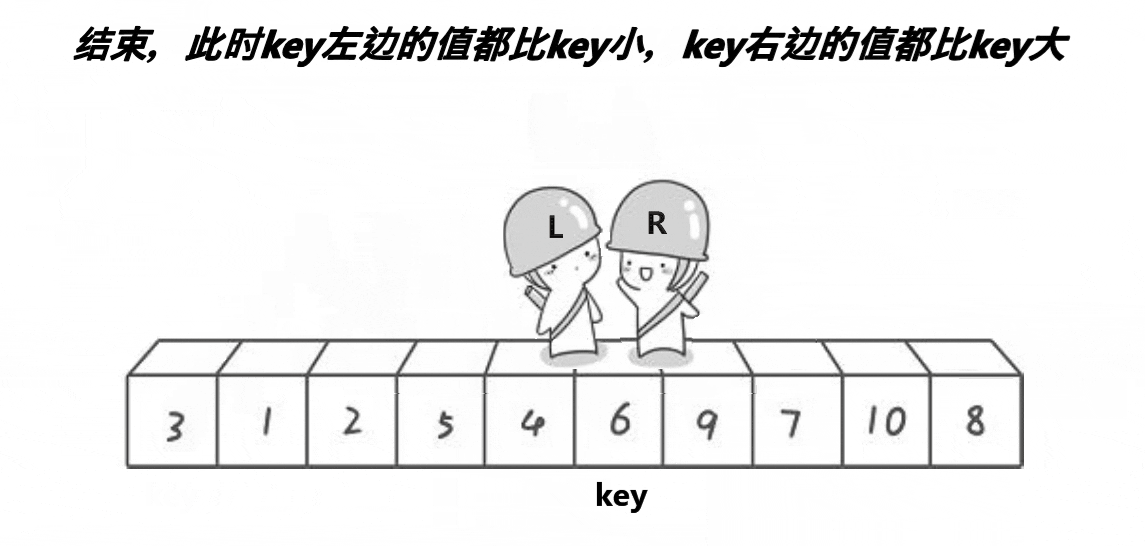
代码实现：

void QuickSortHoare(int* a, int begin, int end)
{
    // begin为首元素下标，end为尾元素下标
    if (begin >= end)
    {
        return; // 递归结束条件：子数组只有一个元素或为空，不需要排序
    }
    
    int left = begin; // 左指针
    int right = end; // 右指针
    int key = begin; // 选择第一个元素作为基准元素

    while (left < right)
    {
        // 从右侧开始，找到第一个比基准元素小的元素
        while (a[right] >= a[key] && right > left)
        {
            right--;
        }
        // 从左侧开始，找到第一个比基准元素大的元素
        while (a[left] <= a[key] && right > left)
        {
            left++;
        }
        // 如果左指针小于右指针，交换左右指针对应的元素
        if (left < right)
        {
            swap(&a[left], &a[right]);
        }
    }
    
    // 将基准元素放到正确的位置上
    swap(&a[key], &a[left]);
    
    // 对基准元素左侧和右侧的子数组进行递归调用
    QuickSortHoare(a, begin, left - 1);
    QuickSortHoare(a, left + 1, end);
}

---

2、挖坑法

挖坑法是一种简洁的快速排序实现方式，它通过交替移动两个指针，将元素一个个填入坑位的方式来进行划分。与Hoare划分法相比，挖坑法在划分的过程中不需要频繁地交换元素，因此实现上会更为简单。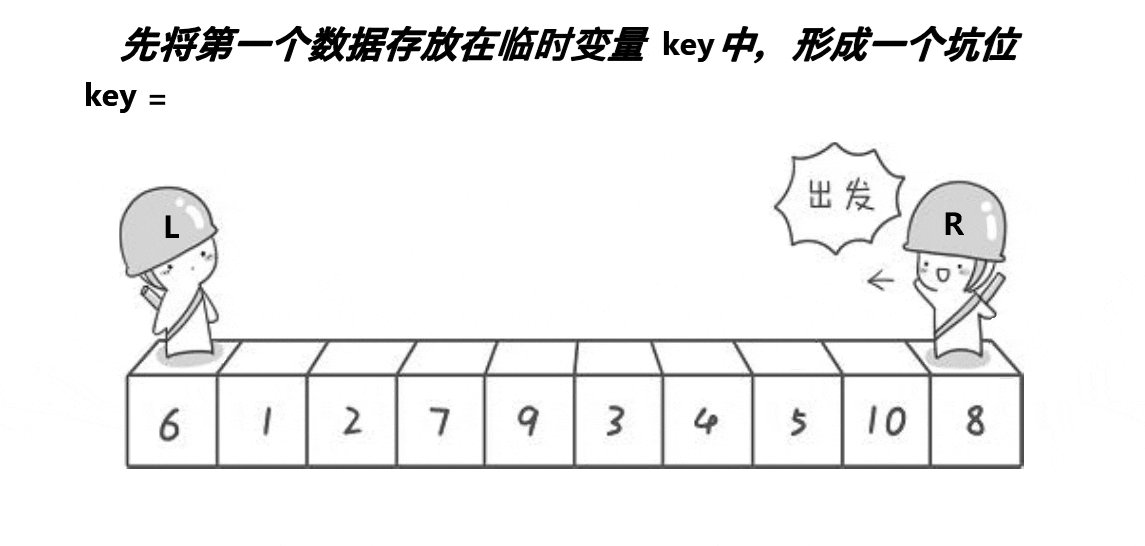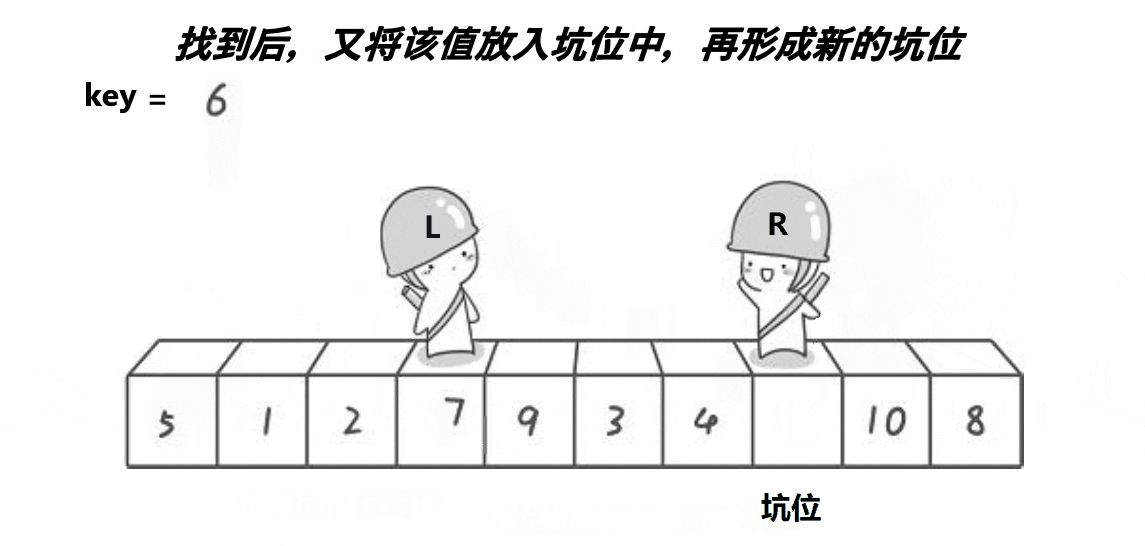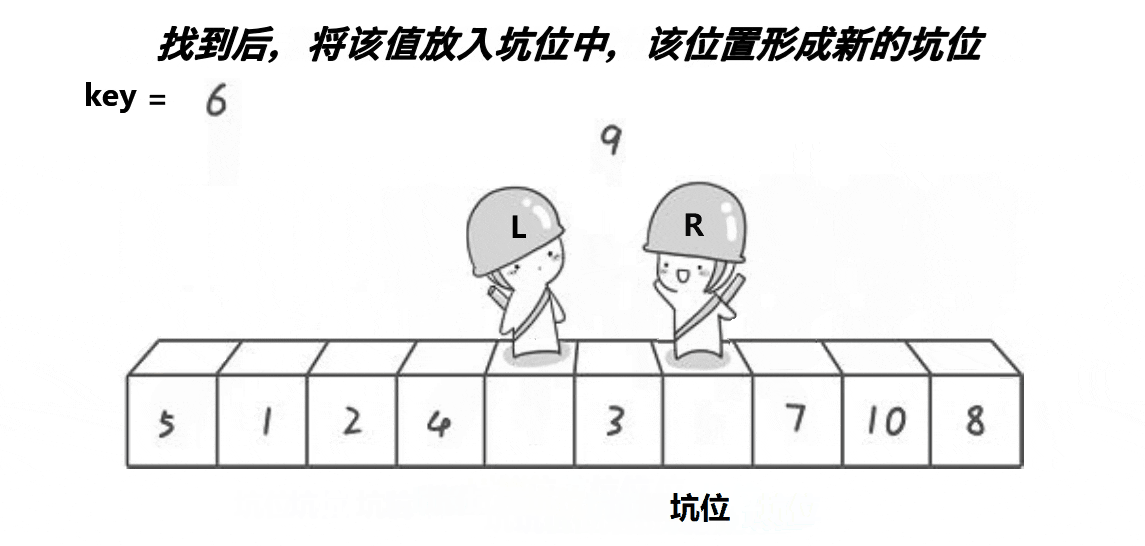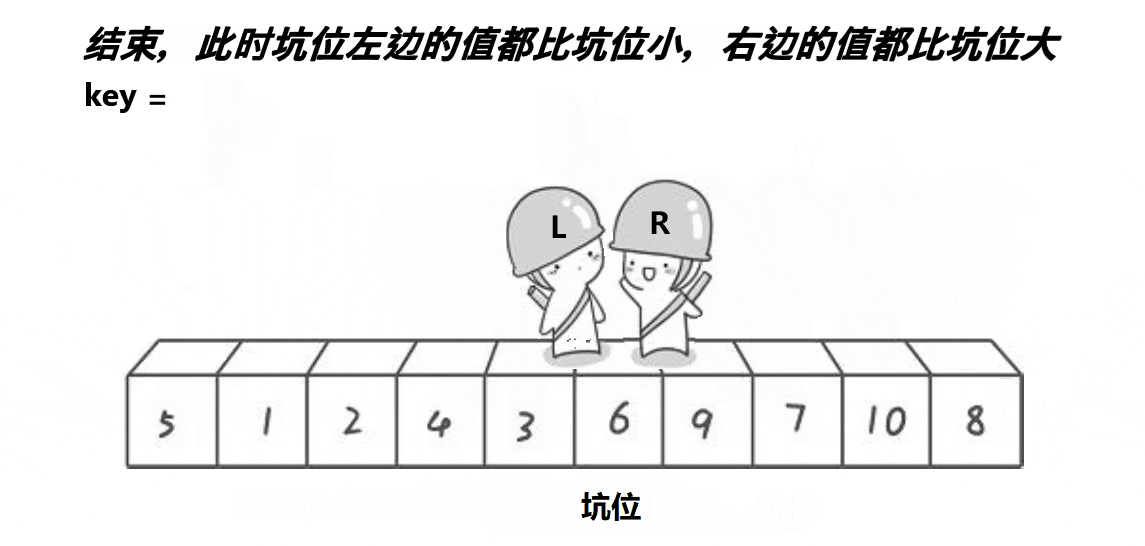

代码实现：?

void QuickSortLomuto(int* a, int begin, int end)
{
    if (begin >= end)
    {
        return; // 递归结束条件：子数组只有一个元素或为空，不需要排序
    }
    
    int curi = begin; // 当前坑位的索引
    int temp = a[begin]; // 枢轴元素的值
    int left = begin; // 左指针
    int right = end; // 右指针

    while (left < right)
    {
        // 从右侧开始，找到第一个比枢轴小的元素的索引
        while (a[right] >= temp && left < right)
        {
            right--;
        }
        a[curi] = a[right]; // 将右指针指向的元素填入当前坑位
        curi = right; // 更新当前坑位的索引
        // 从左侧开始，找到第一个比枢轴大的元素的索引
        while (a[left] <= temp && left < right)
        {
            left++;
        }
        a[curi] = a[left]; // 将左指针指向的元素填入当前坑位
        curi = left; // 更新当前坑位的索引
    }
    
    a[curi] = temp; // 将枢轴元素填入最后一个坑位，确保枢轴元素的位置被确定
    
    // 对枢轴左侧和右侧的子数组进行递归调用
    QuickSortLomuto(a, begin, left - 1);
    QuickSortLomuto(a, left + 1, end);
}

---

3、前后指针法?

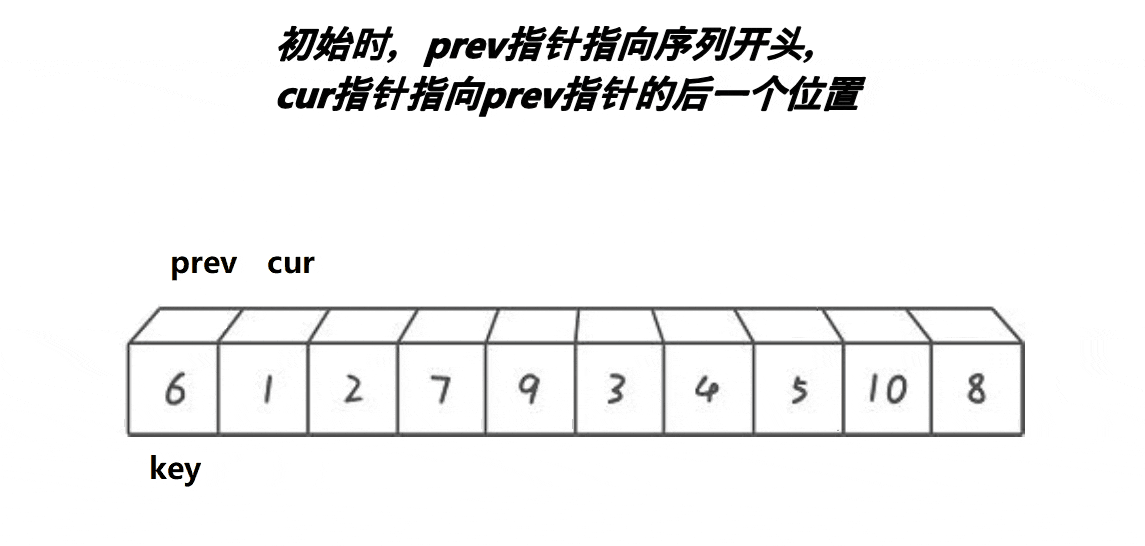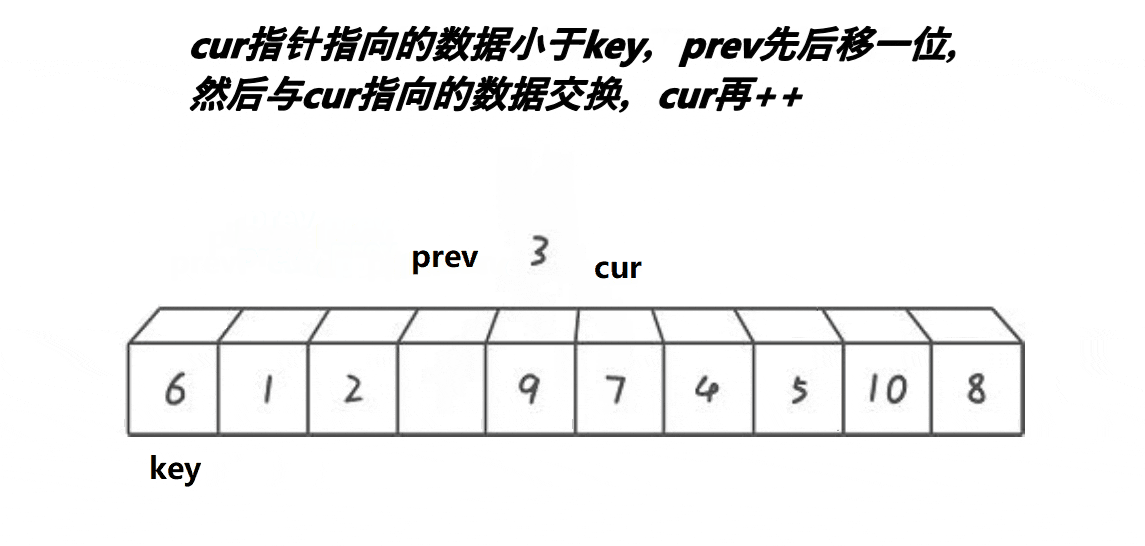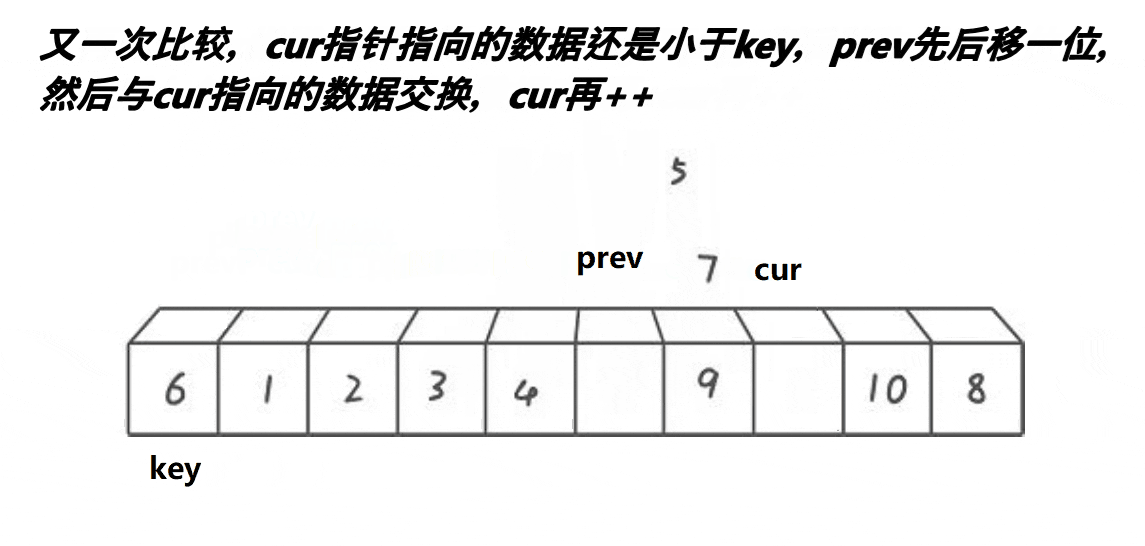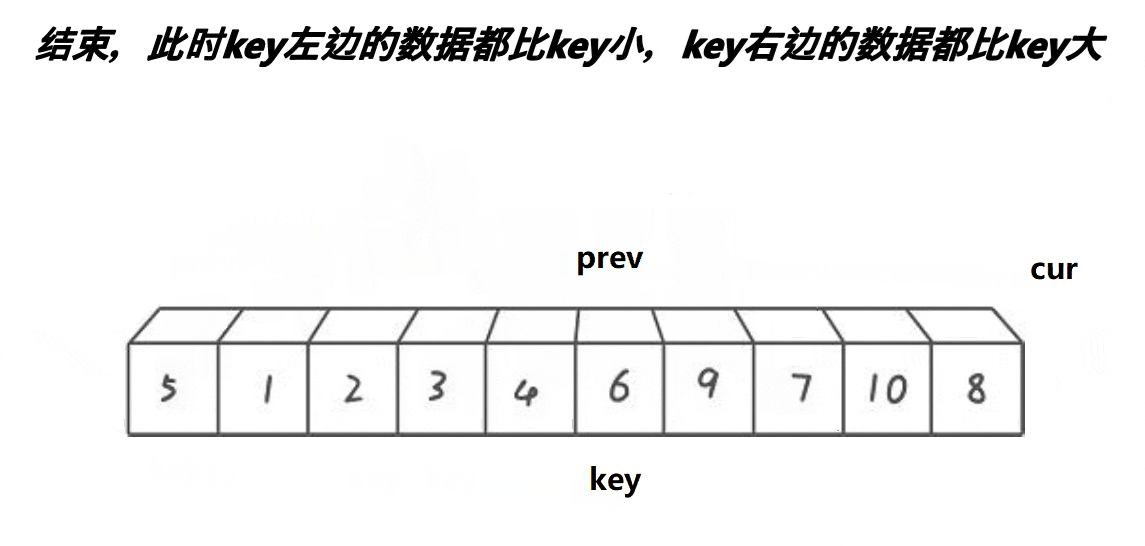
?代码实现：

void QuickSortPB(int* a, int begin, int end)
{
    if(begin > end)
    {
        return; // 递归结束条件：子数组为空，不需要排序
    }
    
    int prev = begin; // prev指针指向枢轴元素的位置
    int cur = prev + 1; // cur指针指向待比较元素的位置
    int key = begin; // 枢轴元素的位置

    // 遍历数组，将小于等于枢轴元素的元素放在prev指针的后面
    while(cur <= end)
    {
        if(a[cur] <= a[key])
        {
            prev++;
            if(cur != prev)
            {
                swap(&a[prev], &a[cur]); // 交换prev指针和cur指针指向的元素
            }
        }
        cur++;
    }
    
    swap(&a[begin], &a[prev]); // 将枢轴元素放到prev指针的位置
    
    // 对枢轴左侧和右侧的子数组进行递归调用
    QuickSortPB(a, begin, prev-1);
    QuickSortPB(a, prev+1, end);
}

---

二、快速排序优化?

"三数取中"的方法是从待排序数组中随机选择三个元素，然后取这三个元素的中间值作为枢轴元素。具体步骤如下：

1. 选择开始位置?begin、结束位置?end?和中间位置?mid，计算?mid = (begin + end) / 2。
2. 比较?a[begin]、a[mid]?和?a[end]?的大小，确定其中的中间值。
3. 将选出的中间值与?a[begin]?进行交换，将中间值放在数组开始的位置，作为枢轴元素。
4. 进行正常的快速排序算法。

通过使用"三数取中"的方法选择枢轴元素，可以尽量避免了最坏情况的发生。最坏的情况是枢轴元素选择的不好，导致每次划分只将数组分成一个很小的部分和一个很大的部分，使得快速排序的时间复杂度退化为O(n^2)。而"三数取中"的方法通过选择一个近似于中位数的元素作为枢轴，能够更平衡地划分数组，减少这种最坏情况的发生，从而提高快速排序的效率。

int GetMidi(int* a, int begin, int end)
{
	int midi = (begin + end) / 2;  // 计算中间位置
	// begin midi end 三个数选中位数
	if (a[begin] < a[midi])  // 如果begin位置的值小于midi位置的值
	{
		if (a[midi] < a[end])  // 如果midi位置的值小于end位置的值
			return midi;  // 返回midi位置
		else if (a[begin] > a[end])  // 如果begin位置的值大于end位置的值
			return begin;  // 返回begin位置
		else
			return end;  // 返回end位置
	}
	else 
	{
		if (a[midi] > a[end])  // 如果midi位置的值大于end位置的值
			return midi;  // 返回midi位置
		else if (a[begin] < a[end])  // 如果begin位置的值小于end位置的值
			return begin;  // 返回begin位置
		else
			return end;  // 返回end位置
	}
}

int QuickSortHoare(int* a, int begin, int end)
{
	int midi = GetMidi(a, begin, end);  // 找到中间位置的索引
	Swap(&a[midi], &a[begin]);  // 交换中间位置的值和起始位置的值

	int left = begin, right = end;  // 设置左右指针
	int keyi = begin;  // 设置基准值索引

	while (left < right)
	{
		// 右边找小
		while (left < right && a[right] >= a[keyi])  // 从右边开始找小于基准值的数
		{
			--right;
		}

		// 左边找大
		while (left < right && a[left] <= a[keyi])  // 从左边开始找大于基准值的数
		{
			++left;
		}

		Swap(&a[left], &a[right]);  // 交换左右指针所指位置的值
	}

	Swap(&a[left], &a[keyi]);  // 将基准值放到中间位置

	return left;  // 返回中间位置的索引
}


void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
		return;  // 如果起始位置大于等于终止位置，则返回

	int keyi = QuickSortHoare(a, begin, end);  // 使用快速排序的Hoare分区函数找到基准值的索引
	QuickSort(a, begin, keyi - 1);  // 对基准值左边的数组进行快速排序
	QuickSort(a, keyi+1, end);  // 对基准值右边的数组进行快速排序
}

---

三、快速排序的非递归实现?

快速排序的非递归实现使用了栈来模拟递归的过程，这样可以避免使用系统栈导致的递归调用过深的问题。

非递归实现的思想如下：

1. 创建一个栈，用于存储待处理子数组的边界。初始时，将整个数组的开始位置和结束位置入栈。

2. 进行循环，直到栈为空。循环的目的是处理栈中的每个子数组。

3. 弹出栈顶的子数组边界，得到开始位置和结束位置。

4. 在子数组中选择枢轴元素，并使用 Hoare 划分方式将子数组划分成两个部分。将划分点的下标入栈，保证后续对其进行排序。

5. 根据划分点的下标更新子数组边界，将左侧子数组的开始位置和结束位置入栈，再将右侧子数组的开始位置和结束位置入栈。注意保证先处理左侧子数组，再处理右侧子数组。

6. 重复步骤 3 到步骤 5，直到栈为空，即所有子数组都被处理完毕。

通过上述步骤，可以将递归的快速排序算法转化为非递归的实现。该实现使用栈来保存待处理的子数组边界，以模拟递归过程。每次处理子数组时，选择一个枢轴元素进行划分，并将划分点的下标入栈。然后根据划分点将子数组分成两部分，分别将左侧和右侧的子数组边界入栈。这样可以确保先处理左侧子数组，再处理右侧子数组，达到快速排序的效果。

代码实现：

typedef int StackDataType;
typedef struct StackNode
{
    StackDataType data;
    struct StackNode* next;
}StackNode;

typedef struct Stack
{
    StackNode* q;
    int size;
}Stack;

void StackInit(Stack* s)
{
    StackNode* head=(StackNode*)malloc(sizeof(StackNode));
    head->next=NULL;
    s->q=head;
    s->size=0;
}

void StackPush(Stack* s,StackDataType x)
{
    StackNode* newnode=(StackNode*)malloc(sizeof(StackNode));
    newnode->data=x;
    newnode->next=s->q->next;
    s->q->next=newnode;  
    s->size++;  
}

int StackEmpty(Stack* s)
{
    if(s->q->next==NULL)
    {
        return 1;
    }
    return 0;
}

StackDataType StackTop(Stack* s)
{
    if(!StackEmpty(s))
    {
        return s->q->next->data;
    }
    else 
    {
        return -1;
    }
}

void StackPop(Stack* s)
{
    if(!StackEmpty(s))
    {
        StackNode* temp=s->q->next;
        s->q->next=s->q->next->next;
        free(temp);
        s->size--;
    }
}

int get_keyi(int *a, int begin, int end)
{
    int left = begin;
    int right = end;
    int key = begin;
    
    while (left < right)
    {
        // 从右侧开始，找到第一个小于 key 的元素
        while (a[right] >= a[key] && left < right)
        {
            right--;
        }
        
        // 从左侧开始，找到第一个大于 key 的元素
        while (a[left] <= a[key] && left < right)
        {
            left++;
        }
        
        // 交换找到的两个元素
        swap(&a[right], &a[left]);
    }
    
    // 将基准值放到中间位置
    swap(&a[key], &a[left]);
    
    return left; // 返回中间位置的索引
}

void QuickSortNR(int* a, int begin, int end)
{
    Stack s;
    StackInit(&s);
    
    // 入栈起始和结束位置
    StackPush(&s, end);
    StackPush(&s, begin);
    
    int left, mid, right;
    
    // 当栈不为空时，循环执行
    while (!StackEmpty(&s))
    {
        left = StackTop(&s);
        StackPop(&s);
        right = StackTop(&s);
        StackPop(&s);
        
        // 如果左边界小于右边界，进行划分
        if (left < right)
        {
            mid = get_keyi(a, left, right);
        }
        
        // 将左边未排序的部分入栈
        if (left < mid - 1)
        {
            StackPush(&s, mid - 1);
            StackPush(&s, left);
        }
        
        // 将右边未排序的部分入栈
        if (right > mid + 1)
        {
            StackPush(&s, right);
            StackPush(&s, mid + 1);
        }
    }
}