MATLAB - 移动机器人运动学方程

发布时间：2024年01月18日

系列文章目录

前言

详细了解移动机器人运动学方程，包括独轮车、自行车、差动驱动和阿克曼模型。本主题涵盖了每种运动模型的变量和特定方程 [1]。有关使用这些模型模拟不同移动机器人的示例，请参阅模拟移动机器人的不同运动模型。

一、变量概述

机器人状态用三元素向量表示： [x y θ]。

对于给定的机器人状态

x: 以米为单位的全局车辆 x 位置
y: 全局车辆的 y 位置，以米为单位
θ: 全局车辆航向，单位为弧度

对于阿克曼运动学，状态还包括转向角：

ψ: 车辆转向角，单位为弧度

独轮车、自行车和差速驱动模型共享一个通用控制输入，该输入接受以下内容：

v: 车辆速度，单位为米/秒
ω: 车辆角速度，单位为弧度/秒

运动学方程中的其他变量包括

r: 车轮半径，单位米
$\dot{\phi }$ ?: 车轮速度（弧度/秒
d: 轨道宽度（米
l: 轮距（米
ψ: 车辆转向角，单位为弧度

二、独轮车运动学

独轮车运动学方程使用 unicycleKinematics 对象对围绕中心轴转动的单个滚动车轮进行建模。

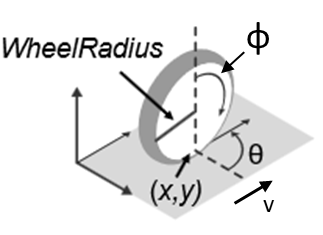
单车模型状态为 [x y θ]。

2.1 变量

x: 以米为单位的全局车辆 x 位置
y: 全局车辆的 y 位置，以米为单位
θ: 全局车辆航向，单位为弧度
$\dot{\phi }$ : 车轮速度（米/秒
r: 车轮半径（米
v: 车速（米/秒
ω: 车辆航向角速度（弧度/秒

2.2 运动方程

根据 VehicleInputs 的名-值参数，您可以只输入车轮速度，也可以输入车辆速度和航向角速度。输入的这种变化会影响方程。

车轮速度方程

$\begin{bmatrix}\dot{x}\\\dot{y}\\\dot{\theta}\end{bmatrix}=\begin{bmatrix}r\cos(\theta)&0\\r\sin(\theta)&0\\0&1\end{bmatrix}\begin{bmatrix}\dot{\phi}\\\omega\end{bmatrix}$

车速和转向率方程（广义）

当一般化输入为速度 v=r $\dot{\phi }$ ?和车辆航向角速度 ω 时，方程简化为

$\begin{bmatrix}\dot{x}\\\dot{y}\\\dot{\theta}\end{bmatrix}=\begin{bmatrix}\cos(\theta)&0\\\sin(\theta)&0\\0&1\end{bmatrix}\begin{bmatrix}\nu\\\omega\end{bmatrix}$

三、自行车运动学

自行车运动学方程模拟的是一种类似汽车的车辆，它使用 bicycleKinematics 对象将前转向角作为控制输入。

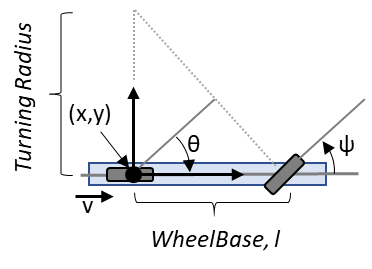
自行车模型状态为 [x y θ]。

3.1 变量

x: 以米为单位的全局车辆 x 位置
y: 全局车辆 y 位置，以米为单位
θ: 全局车辆航向，单位为弧度
l: 轮距，单位米
ψ: 车辆转向角，单位为弧度
v: 车辆速度（米/秒
ω: 车辆航向角速度（弧度/秒

3.2 运动方程

根据 VehicleInputs 的名-值参数，您可以将车速输入为转向角或航向角速度。输入的这种变化会影响方程。

转向角方程

$\begin{bmatrix}\dot{x}\\\dot{y}\\\dot{\theta}\end{bmatrix}=\begin{bmatrix}cos(\theta)&0\\sin(\theta)&0\\\frac{\tan(\psi)}l&1\end{bmatrix}\begin{bmatrix}\nu\\\omega\end{bmatrix}$

车速与航向率公式（通用格式）

在这种广义格式中，航向率 ω 与转向角 ψ 的关系式为 $\omega=\frac{\nu}{l}\mathrm{tan}\psi$ . 然后，ODE 简化为

$\begin{bmatrix}\dot{x}\\\dot{y}\\\dot{\theta}\end{bmatrix}=\begin{bmatrix}\cos(\theta)&0\\\sin(\theta)&0\\0&1\end{bmatrix}\begin{bmatrix}v\\\omega\end{bmatrix}$ ?

四、差动驱动运动学

差速驱动运动学方程使用差速驱动运动学对象对车辆进行建模，其中左右两侧的车轮可以独立旋转。?

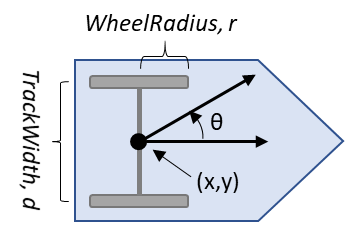
差分驱动模型状态为 [x y θ]。

4.1 变量

x: 全局车辆 x 位置，以米为单位
y: 全局车辆 y 位置，以米为单位
θ: 全局车辆航向，单位为弧度
$\dot{\phi}_L$ : 左轮速度（米/秒
$\dot{\phi}_R$ : 右轮速度（米/秒
r: 车轮半径（米
d: 轨道宽度（米
v: 车速（米/秒
ω: 车辆航向角速度（弧度/秒

4.2 运动方程

根据 VehicleInputs 的名-值参数，您可以将车轮速度输入为转向角或航向角速度。这种输入变化会影响方程。

车轮速度方程

$\begin{bmatrix}\dot{x}\\\dot{y}\\\dot{\theta}\end{bmatrix}=\begin{bmatrix}\dfrac{r}{2}\cos(\theta)&\dfrac{r}{2}\cos(\theta)\\\dfrac{r}{2}\sin(\theta)&\dfrac{r}{2}\sin(\theta)\\-r/2d&r/2d\end{bmatrix}\begin{bmatrix}\dot{\phi}_L\\\dot{\phi}_R\end{bmatrix}$

车速和转向率公式（通用格式）

在广义格式中，输入为速度 $\nu=\frac{r}{2}\left(\dot{\phi}R+\dot{\phi}_{L}\right)$ 和车辆航向角速度 $\omega=\frac{r}{2d}(\dot{\phi}R-\dot{\phi}L)$ 。 ODE 简化为：

$\begin{bmatrix}\dot{x}\\\dot{y}\\\dot{\theta}\end{bmatrix}=\begin{bmatrix}\cos(\theta)&0\\\sin(\theta)&0\\0&1\end{bmatrix}\begin{bmatrix}\nu\\\omega\end{bmatrix}$

五、阿克曼运动学

阿克曼运动学方程使用阿克曼运动学对象对带有阿克曼转向机构的汽车模型进行建模。该方程根据轨道宽度调整车轴轮胎的位置，使轮胎沿着同心圆运动。在数学上，这意味着输入必须是转向航向角速度? $\dot{\psi }$ 没有通用格式。

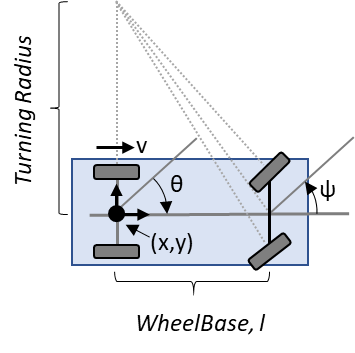
阿克曼模型的状态是 [x y θ ψ]。

5.1 变量

x: 以米为单位的全局车辆 x 位置
y: 全局车辆的 y 位置，以米为单位
θ: 全局车辆航向，单位为弧度
ψ: 车辆转向角，单位为弧度
l: 轮距（米
v: 车辆速度（米/秒

5.2 运动学方程

对于阿克曼运动学模型，ODE 为

$\begin{bmatrix}\dot{x}\\\dot{y}\\\dot{\theta}\\\dot{\psi}\end{bmatrix}=\begin{bmatrix}\cos(\theta)&0\\\sin(\theta)&0\\\tan(\psi)/l&0\\0&1\end{bmatrix}\begin{bmatrix}\nu\\\dot{\psi}\end{bmatrix}$

参考资料

[1] Lynch, Kevin M., and Frank C. Park.?Modern Robotics: Mechanics, Planning, and Control. Cambridge University Press, 2017.

文章来源:https://blog.csdn.net/weixin_46300916/article/details/135591619
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！