Dirichlet Process 4
发布时间:2024年01月23日
每一个样本都有自己对应的,有多少个样本就有多少个
如果有a个相等,那么我们能够相信这a个对应的样本x属于同一类的
要保证能够相等,所以
要从一个离散的分布,即G中产生
所以有如下关系
图模型如下:
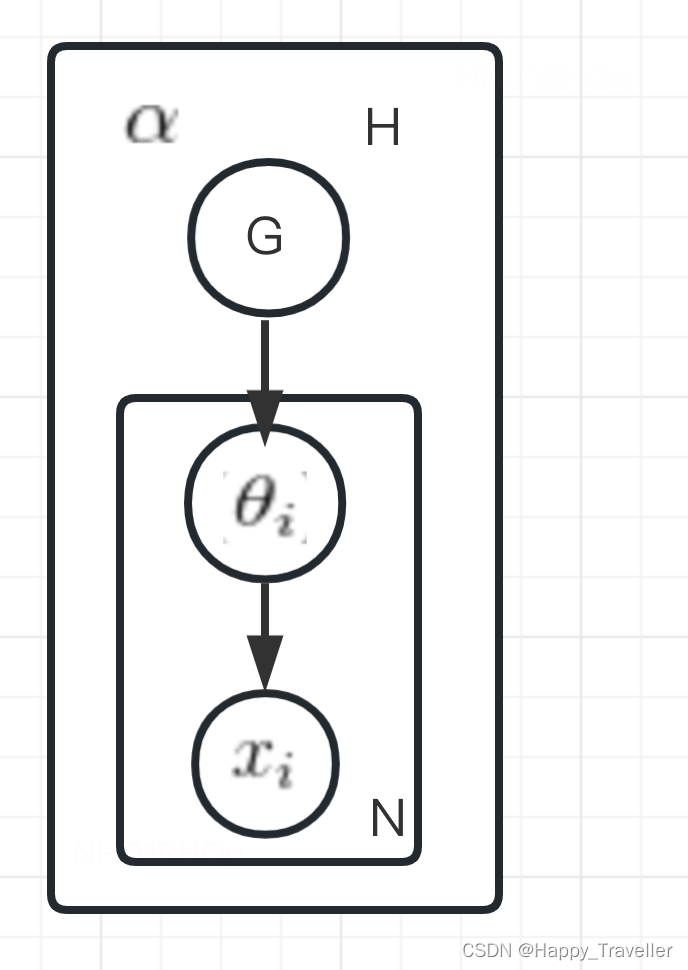
,这里面
,直接将G带入有些困难,这里面使用了狄利克雷分布和多项式分布共轭的性质
可以看到新的DP的base measure?,和之前的H相比,新加了一个离散的项。
文章来源:https://blog.csdn.net/zhangsj1007/article/details/130992626
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 关于标准那些事——第八篇 起步
- 嵌入式软件工程师面试题——2025校招社招通用(二十二)
- 【网络工程师】三层交换机与HSRP
- 如何解决HTTP 404错误,这里给出详细解决办法
- v-if与v-show的区别
- 【Linux install】Ubuntu和win双系统安装及可能遇到的所有问题
- 排序之快速排序
- JAVA|PHP|c#爬虫-1688官网自动以图搜图API接口功能实现
- CAN信号发送与APP SWC组件的Port接口映射与连接
- FreeBSD下安装Jenkins(软件测试集成工具)记录