excel统计分析——CVM正态性检验

发布时间：2023年12月26日

马兴华,张晋昕.数值变量正态性检验常用方法的对比[J].循证医学,2014,14(02):123-128

? ? ? ? CVM检验的思想基本与K-S检验一致，与K-S检验相比，CVM检验统计量度量的是经验累积分布函数和目标累积分布函数的平方距离的积分。就是把每个数据点的差求平方以后相加，得到总的分布偏差，这样就考虑了所有的差异点，而不是像K-S检验那样只考虑一个最大的。实际应用中CVM检验比K-S检验更容易拒绝正态分布假定。要求样本量大于7。

计算步骤如下：

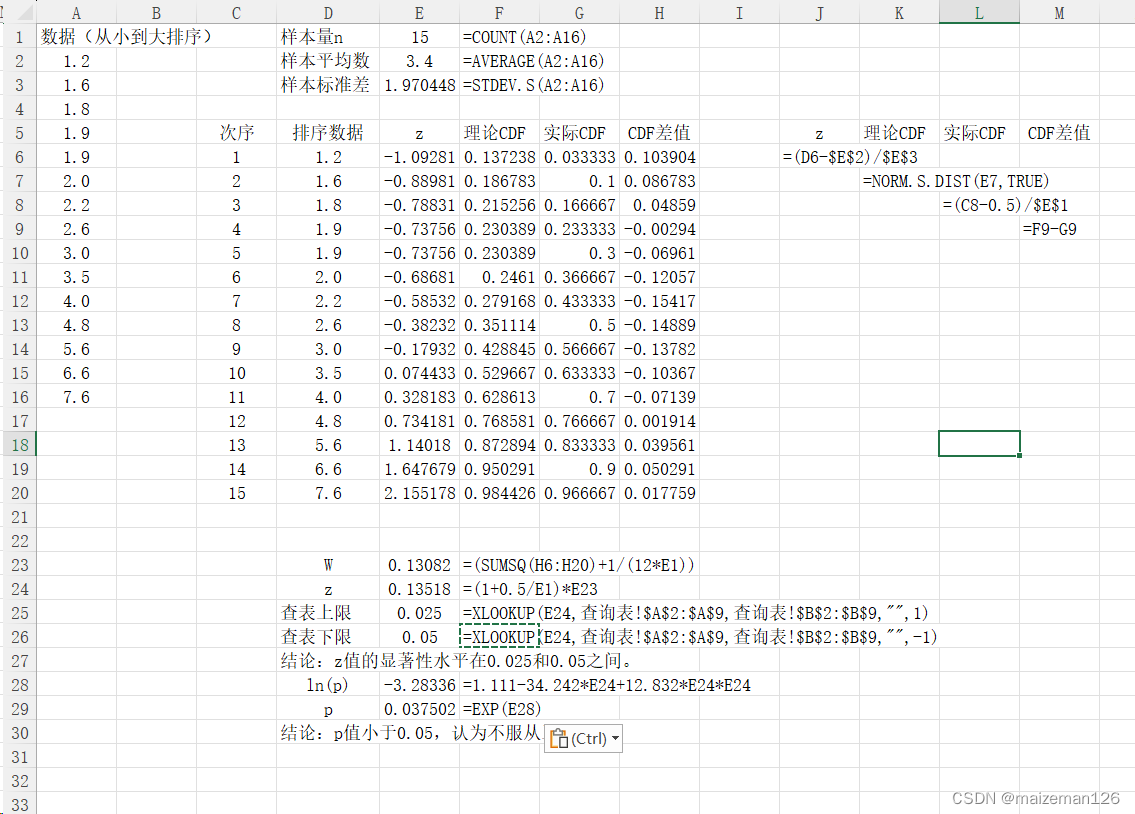
1、将数据从小到大进行排序，形成x1<x2<...<xn。

2、计算统计量：

$W=\sum_{i=1}^{n}(x_{i}-\frac{i-1/2}{n})^{2}+\frac{1}{12n}$

3、将样本数据调整为标准正态分布数据，如下（像R中nortest程序包中cvm.test函数）：

$W=\sum_{i=1}^{n}(\Phi (\frac{x_{i}-\bar{x}}{\sqrt{S^{2}}})-\frac{i-1/2}{n})^{2}+\frac{1}{12n}$

其中，Φ(.)为标准正态分布的累计分布函数， $\frac{i-1/2}{n}$ 为经验分布函数。

4、计算修正统计量z

$z=(1+\frac{0.5}{n})\times W$

5、根据z值计算p值

当z<0.0275时：

$\mathrm{ln}\,(1-p)=-13.953+775.5z-12542.61z^2$

$p=1-e^{-13.953+775.5z-12542.61z^2}$

当0.0275<z<0.051时：

$\mathrm{ln}\,(1-p)=-5.903+179.546z-1515.29z^2$

$p=1-e^{-5.903+179.546z-1515.29z^2}$

当0.051<z<0.092时：

$\textup{\textrm{}ln}\,p=0.886-31.62z+10.897z^2$

$p=e^{0.886-31.62z+10.897z^2}$

当z>0.092时：

$\mathrm{ln}\,p=1.111-34.242z+12.832z^2$

$p=e^{1.111-34.242z+12.832z^2}$

excel操作步骤如下：

文章来源:https://blog.csdn.net/maizeman126/article/details/135219131
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！