二分算法--x的平方根

?个人主页：Lei宝啊?

愿所有美好如期而遇

---

二分算法前言

二分算法原理超详细讲解(包括暴力求解，朴素二分查找，二分查找左右端点)：二分查找(非朴素)--在排序数组中查找元素的第一个和最后一个位置https://blog.csdn.net/m0_74824254/article/details/135306648?spm=1001.2014.3001.5501

本题链接?

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

输入描述

输入一个数，求其平方根，不允许使用sqrt库函数，因为我们要模拟sqrt，

接口为int mySqrt(int x)

输出描述

我们以8为例子，要求8的平方根，根号2明显求不整，所以要去掉小数部分，返回整数部分。

算法分析

算法一：暴力求解

我们直接定义变量 i 从 0 开始for循环遍历，直到平方大于x，我们返回 i - 1。

算法二：二分算法

这个属于查找右端点

我们首先要分区间，一个区间内下标的平方小于等于x，一个区间内下标的平方大于x，我们要的是小于等于区间的最右边那个数的下标。(lhs意为left side hand即左手边，rhs意为right side hand即右手边)

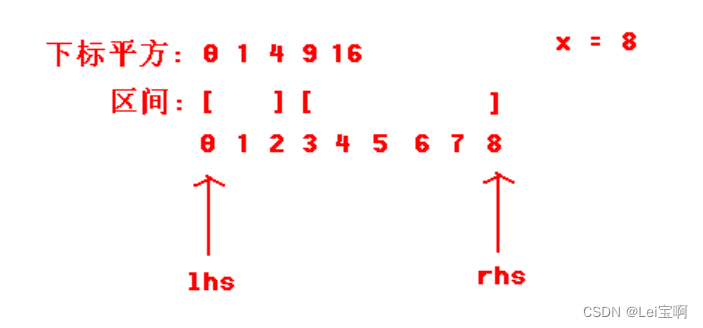
我们定义mid以及num，num = mid * mid代表平方，所以有

• 小于等于区间 ，if(num <= x) lhs = mid;
• 大于区间，if(num > x ) rhs = mid - 1;

那么为什么lhs 不是 mid + 1呢？当我们的mid位于小于等于区间的右边界处，此时lhs = mid + 1,那么lhs就出了小于等于区间，我们也就得不到想要的下标了。

要知道我们可以预见的一个事实就是，lhs是不会越过小于等于区间的，因为只有num <= x，lhs才会更新到mid处，而这样的mid都在区间内，也就是说，只有等到rhs越过大于区间使得lhs == rhs，此时我们循环结束，得到我们想要的下标，我们将其返回。

我们将上面分区间理解后，还没有完，二分算法有一些细节，如果不注意，那么就会出现死循环。

细节一:

while循环,不同于朴素的二分算法，这里循环结束的条件是lhs < rhs，一个原因是没有必要，另一个原因是如果我们选择去判断相等，会出现死循环。

细节二:

mid的值，不同于朴素二分算法，如果我们选择mid = lhs + (rhs - lhs) / 2；同样会出现死循环。

上述两个细节的详细原因我们在二分算法前言的链接里详细提到，这里不多赘述。

解题源码

class Solution {
public:
    int mySqrt(int x) 
    {
        //注意范围
        long long lhs = 0, rhs = x;
        long long mid = lhs + (rhs - lhs + 1) / 2, num = mid * mid;
        
        //细节一
        while(lhs < rhs)
        {
            //分区间
            if(num <= x) lhs = mid;
            else rhs = mid - 1;

            //细节二
            mid = lhs + (rhs - lhs + 1) / 2;
            num = mid * mid;
        }

        return lhs;
    }
};