1.2LeetCode两个链表相加，两数之和（map映射），滑动窗口，链表相交，前K个出现的数，三数之和，对链表进行排序（插入，归并）

两个链表相加?

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode *head = nullptr, *tail = nullptr;
        int carry = 0;
        while (l1 || l2) {
            int n1 = l1 ? l1->val: 0;
            int n2 = l2 ? l2->val: 0;
            int sum = n1 + n2 + carry;
            if (!head) {
                head = tail = new ListNode(sum % 10);
            } else {
                tail->next = new ListNode(sum % 10);
                tail = tail->next;
            }
            carry = sum / 10;
            if (l1) {
                l1 = l1->next;
            }
            if (l2) {
                l2 = l2->next;
            }
        }
        if (carry > 0) {
            tail->next = new ListNode(carry);
        }
        return head;
    }
};

两数之和

auto返回map，返回的是一个键值对，要用下标还要指定first以及second

m[nums[i]]=i构建映射关系

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        map<int,int>m;
        for(int i=0;i<nums.size();i++){
            auto it=m.find(target-nums[i]);
            if(it!=m.end())return{it->second,i};
            m[nums[i]]=i;
        }
        return{};
    }
};

滑动窗口 （队列）

这道题主要用到思路是：滑动窗口

什么是滑动窗口？

其实就是一个队列,比如例题中的 abcabcbb，进入这个队列（窗口）为 abc 满足题目要求，当再进入 a，队列变成了 abca，这时候不满足要求。所以，我们要移动这个队列！

如何移动？

我们只要把队列的左边的元素移出就行了，直到满足题目要求！

一直维持这样的队列，找出队列出现最长的长度时候，求出解！

时间复杂度：O(n)

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        if(s.size() == 0) return 0;
        unordered_set<char> lookup;
        int maxStr = 0;
        int left = 0;
        for(int i = 0; i < s.size(); i++){
            while (lookup.find(s[i]) != lookup.end()){
                lookup.erase(s[left]);
                left ++;
            }
            maxStr = max(maxStr,i-left+1);
            lookup.insert(s[i]);
    }
        return maxStr;
        
    }
};

之所以用set而不用queue，是因为来了新元素后，queue无法第一时间确定队列窗口里是否有这个元素，必须要遍历完队列才能直到有没有，所以就用哈希表，就可以直接查询到到底有没有

链表相交

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if(headA==nullptr||headB==nullptr)return nullptr;
        ListNode* pa=headA,*pb=headB;
        while(pa!=pb){
            pa=pa==nullptr?headB:pa->next;
            pb=pb==nullptr?headA:pb->next;
        }
        return pa;
    }
};

前K个出现的数

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        map<int,int>m;
        for(int i=0;i<nums.size();i++)m[nums[i]]++;
        struct cmp{
            bool operator()(pair<int,int>&p1,pair<int,int>&p2){
                return p1.second>p2.second;
            }
        };
        priority_queue<pair<int,int>,vector<pair<int,int>>,cmp>q;
        for(auto a:m){
            q.push(a);
            if(q.size()>k){q.pop();}
        }
        vector<int>res;
        while(!q.empty()){
            res.push_back(q.top().first);
            q.pop();
        }
        return res;
    }
};

三数之和

特判，对于数组长度 nnn，如果数组为 nullnullnull 或者数组长度小于 333，返回 [][][]。
对数组进行排序。
遍历排序后数组：
若 nums[i]>0nums[i]>0nums[i]>0：因为已经排序好，所以后面不可能有三个数加和等于 000，直接返回结果。
对于重复元素：跳过，避免出现重复解
令左指针 L=i+1L=i+1L=i+1，右指针 R=n?1R=n-1R=n?1，当 L<RL<RL<R 时，执行循环：
当 nums[i]+nums[L]+nums[R]==0nums[i]+nums[L]+nums[R]==0nums[i]+nums[L]+nums[R]==0，执行循环，判断左界和右界是否和下一位置重复，去除重复解。并同时将 L,RL,RL,R 移到下一位置，寻找新的解
若和大于 000，说明 nums[R]nums[R]nums[R] 太大，RRR 左移
若和小于 000，说明 nums[L]nums[L]nums[L] 太小，LLL 右移

三指针，一个指针确定一个数，先动一个指针，由那个指针确定一个区间（在右边），然后左右指针分别在那个区间的两侧，开始扫描

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        vector<vector<int>> ans;
        // 枚举 a
        for (int first = 0; first < n; ++first) {
            // 需要和上一次枚举的数不相同
            if (first > 0 && nums[first] == nums[first - 1]) {
                continue;
            }
            // c 对应的指针初始指向数组的最右端
            int third = n - 1;
            int target = -nums[first];
            // 枚举 b
            for (int second = first + 1; second < n; ++second) {
                // 需要和上一次枚举的数不相同
                if (second > first + 1 && nums[second] == nums[second - 1]) {
                    continue;
                }
                // 需要保证 b 的指针在 c 的指针的左侧
                while (second < third && nums[second] + nums[third] > target) {
                    --third;
                }
                // 如果指针重合，随着 b 后续的增加
                // 就不会有满足 a+b+c=0 并且 b<c 的 c 了，可以退出循环
                if (second == third) {
                    break;
                }
                if (nums[second] + nums[third] == target) {
                    ans.push_back({nums[first], nums[second], nums[third]});
                }
            }
        }
        return ans;
    }
};

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        
        n=len(nums)
        res=[]
        if(not nums or n<3):
            return []
        nums.sort()
        res=[]
        for i in range(n):
            if(nums[i]>0):
                return res
            if(i>0 and nums[i]==nums[i-1]):
                continue
            L=i+1
            R=n-1
            while(L<R):
                if(nums[i]+nums[L]+nums[R]==0):
                    res.append([nums[i],nums[L],nums[R]])
                    while(L<R and nums[L]==nums[L+1]):
                        L=L+1
                    while(L<R and nums[R]==nums[R-1]):
                        R=R-1
                    L=L+1
                    R=R-1
                elif(nums[i]+nums[L]+nums[R]>0):
                    R=R-1
                else:
                    L=L+1
        return res

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int n=nums.size();
        sort(nums.begin(),nums.end());
        vector<vector<int>>ans;
        for(int first=0;first<n;first++){
            if(nums[first]>0)break;
            if(first>0&&nums[first]==nums[first-1])continue;
            int third=n-1,target=-nums[first];
            for(int second=first+1;second<n;second++){
                if(second>first+1&&nums[second]==nums[second-1])continue;
                while(second<third&&nums[second]+nums[third]>target){
                    third--;
                }
                if(nums[second]+nums[third]==target){
                    ans.push_back({nums[first],nums[second],nums[third]});
                }
                if(second==third)break;
            }
        }
        return ans;
    }
};

对联表进行插入排序

class Solution {
public:
    ListNode* insertionSortList(ListNode* head) {
        if (head == nullptr) {
            return head;
        }
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* lastSorted = head;
        ListNode* curr = head->next;
        while (curr != nullptr) {
            if (lastSorted->val <= curr->val) {
                lastSorted = lastSorted->next;
            } else {
                ListNode *prev = dummyHead;
                while (prev->next->val <= curr->val) {
                    prev = prev->next;
                }
                lastSorted->next = curr->next;
                curr->next = prev->next;
                prev->next = curr;
            }
            curr = lastSorted->next;
        }
        return dummyHead->next;
    }
};

对链表进行插入排序的具体过程如下。

首先判断给定的链表是否为空，若为空，则不需要进行排序，直接返回。

创建哑节点 dummyHead，令 dummyHead.next = head。引入哑节点是为了便于在 head 节点之前插入节点。

维护 lastSorted 为链表的已排序部分的最后一个节点，初始时 lastSorted = head。

维护 curr 为待插入的元素，初始时 curr = head.next。

比较 lastSorted 和 curr 的节点值。

若 lastSorted.val <= curr.val，说明 curr 应该位于 lastSorted 之后，将 lastSorted 后移一位，curr 变成新的 lastSorted。

否则，从链表的头节点开始往后遍历链表中的节点，寻找插入 curr 的位置。令 prev 为插入 curr 的位置的前一个节点，进行如下操作，完成对 curr 的插入：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* insertionSortList(ListNode* head) {
        if(head==nullptr){return nullptr;}
        ListNode*phead=new ListNode(0);
        phead->next=head;//phead的目的是能够在链表的最前面插入元素
        ListNode*last=head;
        ListNode*curr=head->next;
        while(curr!=nullptr){
            if(last->val<=curr->val){
                last=last->next;//原本在逻辑以及物理上就是连续的，所以可以直接移位
            }else{
                ListNode*prev=phead;
                while(prev->next->val<=curr->val){
                    prev=prev->next;
                }//循环条件是p->next,这样停止时，p是小于的，p->next是大于的，那么中间就是应该在的位置
                last->next=curr->next;
                curr->next=prev->next;
                prev->next=curr;
            }
            curr=last->next;//curr逻辑上就应该是Last的下一个位置，即未排序的下一个位置
        }
        return phead->next;
    }
};

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* insertionSortList(ListNode* head) {
        if(!head)return head;
        ListNode*phead=new ListNode(0);
        phead->next=head;
        ListNode*last=head;
        ListNode*curr=head->next;
        while(curr){
            if(last->val<=curr->val){
                last=last->next;
            }else{
                ListNode*prev=phead;
                while(prev->next->val<=curr->val){
                    prev=prev->next;
                }
                last->next=curr->next;//last在物理上是没动的，只是在逻辑上动了，即因为此时的curr前移了，所以last在逻辑上后退了
                curr->next=prev->next;
                prev->next=curr;
            }
            curr=last->next;//curr就是last逻辑上的后一个

        }
        return phead->next;
    }
};

last指向的，应该是已排序序列当中最大的那个元素

排序链表

用插入排序的结果：

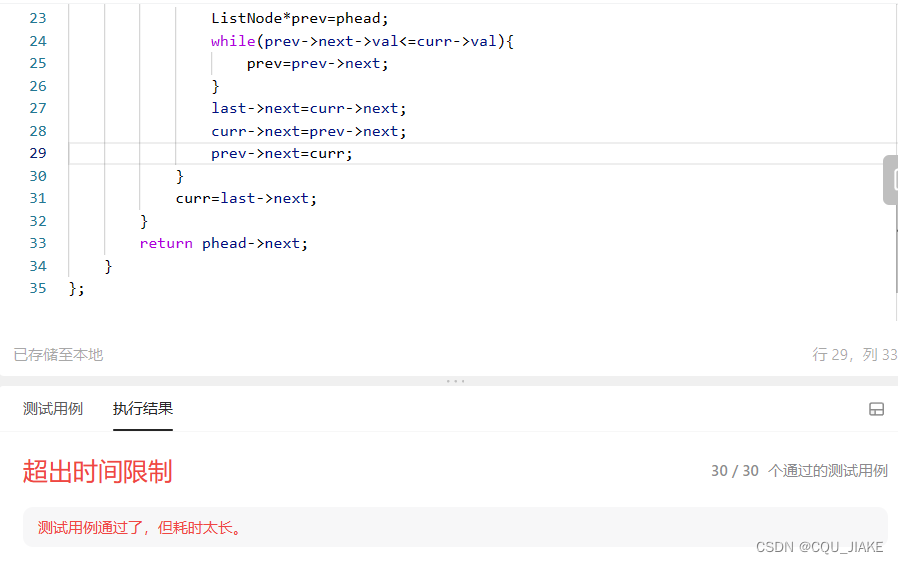
?用归并排序

class Solution {
public:
    ListNode* sortList(ListNode* head) {
        return sortList(head, nullptr);
    }

    ListNode* sortList(ListNode* head, ListNode* tail) {
        if (head == nullptr) {
            return head;
        }
        if (head->next == tail) {
            head->next = nullptr;
            return head;
        }
        ListNode* slow = head, *fast = head;
        while (fast != tail) {
            slow = slow->next;
            fast = fast->next;
            if (fast != tail) {
                fast = fast->next;
            }
        }
        ListNode* mid = slow;
        return merge(sortList(head, mid), sortList(mid, tail));
    }

    ListNode* merge(ListNode* head1, ListNode* head2) {
        ListNode* dummyHead = new ListNode(0);
        ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
        while (temp1 != nullptr && temp2 != nullptr) {
            if (temp1->val <= temp2->val) {
                temp->next = temp1;
                temp1 = temp1->next;
            } else {
                temp->next = temp2;
                temp2 = temp2->next;
            }
            temp = temp->next;
        }
        if (temp1 != nullptr) {
            temp->next = temp1;
        } else if (temp2 != nullptr) {
            temp->next = temp2;
        }
        return dummyHead->next;
    }
};