基于HyperOpt实现TPE优化

基于HyperOpt实现TPE优化

Hyperopt是目前最为通用的贝叶斯优化器之一，它集成了随机搜索、模拟退火和TPE（Tree-structured Parzen Estimator Approach）等多种优化算法。相较于Bayes_opt，Hyperopt更先进、更现代、维护更好，也是我们最常用来实现TPE方法的优化器。在实际应用中，基于高斯混合模型的TPE通常比基于高斯过程的贝叶斯优化更高效地获得更优结果，在AutoML领域也得到了广泛应用。

1 定义目标函数

Notes:

1. 目标函数的输入必须是符合hyperopt规定的字典;
2. Hyperopt只支持寻找𝑓(𝑥)的最小值，不支持寻找最大值。

def hyperopt_objective(params):
    
    #定义评估器
    #需要搜索的参数需要从输入的字典中索引出来
    #不需要搜索的参数，可以是设置好的某个值
    #在需要整数的参数前调整参数类型
    reg = RFR(n_estimators = int(params["n_estimators"])
              ,max_depth = int(params["max_depth"])
              ,max_features = int(params["max_features"])
              ,min_impurity_decrease = params["min_impurity_decrease"]
              ,random_state=1412
              ,verbose=False
              ,n_jobs=-1)
    
    #交叉验证结果，输出负根均方误差（-RMSE）
    cv = KFold(n_splits=5,shuffle=True,random_state=1412)
    validation_loss = cross_validate(reg,X,y
                                     ,scoring="neg_root_mean_squared_error"
                                     ,cv=cv
                                     ,verbose=False
                                     ,n_jobs=-1
                                     ,error_score='raise'
                                    )
    
    #最终输出结果，由于只能取最小值，所以必须对（-RMSE）求绝对值
    #以求解最小RMSE所对应的参数组合
    return np.mean(abs(validation_loss["test_score"]))

2 定义参数空间

在hyperopt中，我们使用特殊的字典形式来定义参数空间，其中键值对上的键可以任意设置，只要与目标函数中索引参数的键一致即可，键值对的值则是hyperopt独有的hp函数，包括了：
hp.quniform(“参数名称”, 下界, 上界, 步长) - 适用于均匀分布的浮点数

hp.uniform(“参数名称”,下界, 上界) - 适用于随机分布的浮点数


hp.randint(“参数名称”,上界) - 适用于[0,上界)的整数，区间为前闭后开


hp.choice(“参数名称”,[“字符串1”,“字符串2”,…]) - 适用于字符串类型，最优参数由索引表示


hp.choice(“参数名称”,[*range(下界，上界，步长)]) - 适用于整数型，最优参数由索引表示


hp.choice(“参数名称”,[整数1,整数2,整数3,…]) - 适用于整数型，最优参数由索引表示


hp.choice(“参数名称”,[“字符串1”,整数1,…]) - 适用于字符与整数混合，最优参数由索引表示

在hyperopt的说明当中，并未明确参数取值范围空间的开闭，根据实验，如无特殊说明，hp中的参数空间定义方法应当都为前闭后开区间。

param_grid_simple = {'n_estimators': hp.quniform("n_estimators",80,100,1)
                     , 'max_depth': hp.quniform("max_depth",10,25,1)
                     , "max_features": hp.quniform("max_features",10,20,1)
                     , "min_impurity_decrease":hp.quniform("min_impurity_decrease",0,5,1)
                    }

由于hp.choice最终会返回最优参数的索引，容易与数值型参数的具体值混淆，而hp.randint又只能够支持从0开始进行计数，因此我们常常会使用quniform获得均匀分布的浮点数来替代整数。对于需要取整数的参数值，如果采用quniform方式构筑参数空间，则需要在目标函数中使用int函数限定输入类型。例如，在范围[0,5]中取值时，可以取出[0.0, 1.0, 2.0, 3.0,…]这种均匀浮点数，在输入目标函数时，则必须确保参数值前存在int函数。当然，如果使用hp.choice则不会存在该问题。

3 定义优化目标函数的具体流程

一旦我们确定了目标函数和参数空间，就可以开始优化过程了。在Hyperopt中，我们使用的优化基础功能是fmin。在fmin中，我们可以自定义使用的代理模型（参数algo），通常有两种选择：tpe.suggest代表TPE方法，rand.suggest代表随机网格搜索方法。我们还可以使用partial功能来修改算法涉及的具体参数，包括模型使用的初始观测值数量（参数n_start_jobs）以及在计算采集函数值时考虑的样本数量（参数n_EI_candidates）。当然，我们也可以不填写这些参数，使用默认值。

此外，Hyperopt还有两个值得注意的功能：trials和early_stop_fn。trials记录了整个迭代过程中的实验信息，我们通常会使用从hyperopt库导入的Trials()方法来初始化。优化完成后，我们可以从保存好的trials中查看损失、参数等各种中间信息。early_stop_fn通常使用从hyperopt库导入的no_progress_loss()方法，其中可以输入一个数字n，表示当损失连续n次没有下降时，让算法提前停止。由于贝叶斯方法的随机性较高，当样本量不足时需要多次迭代才能够找到最优解，因此一般no_progress_loss()中的数值不会设置得太高。由于数据量较少，我设置了一个较高的值来避免迭代停止太早。

def param_hyperopt(max_evals=100):
    
    #保存迭代过程
    trials = Trials()
    
    #设置提前停止
    early_stop_fn = no_progress_loss(100)
    
    #定义代理模型
    #algo = partial(tpe.suggest, n_startup_jobs=20, n_EI_candidates=50)
    params_best = fmin(hyperopt_objective #目标函数
                       , space = param_grid_simple #参数空间
                       , algo = tpe.suggest #代理模型你要哪个呢？
                       #, algo = algo
                       , max_evals = max_evals #允许的迭代次数
                       , verbose=True
                       , trials = trials
                       , early_stop_fn = early_stop_fn
                      )
    
    #打印最优参数，fmin会自动打印最佳分数
    print("\n","\n","best params: ", params_best,
          "\n")
    return params_best, trials

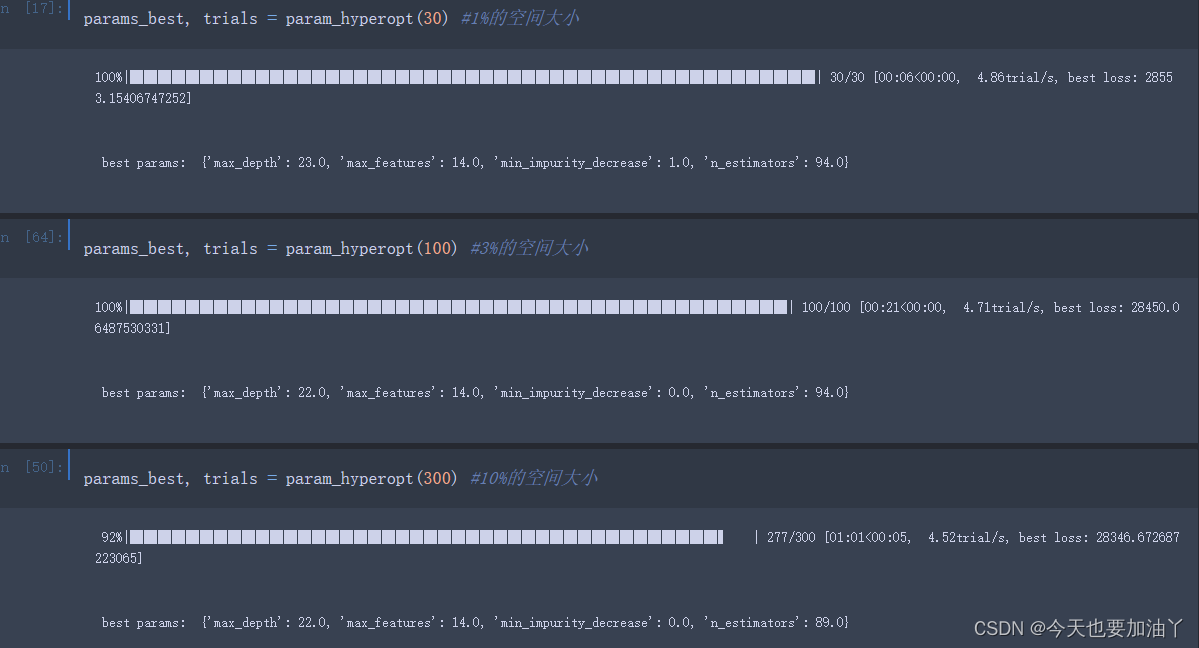
5 执行实际优化流程

计算参数空间