算法 递推 杭州电子科技大学考研机试题 acwing3643上楼梯
发布时间:2023年12月28日
是什么?
? ? ? ?是一种通过利用已知的初始条件和递推关系,逐步推导出更复杂情况的算法。它通常用于解决数列、数值序列或逻辑问题等。
关键要素
-
初始条件:确定初始情况下的解。这是递推算法中的基础情况,通常是已知或容易计算的情况。
-
递推关系:确定如何通过已知的解推导出更复杂情况的解。递推关系通常是一个数学公式或算法规则,描述了问题的演进或变化规律。
-
终止条件:确定递推的结束条件。一旦终止条件满足,算法就会停止递推,并返回最终的解。
例子
计算斐波那契数列的第n项。递推关系:斐波那契数列的第n项(记作F(n))等于前两项的和,即 F(n) = F(n-1)+ F(n-2),其中 F(1) = 1,F(2) = 1。
杭州电子科技大学考研机试题 acwing3643 上楼梯
一个楼梯共有?n级台阶,每次可以走一级或者两级或者三级,问从第?0?级台阶走到第?n级台阶一共有多少种方案。
输入格式
一个整数?N。
输出格式
一个整数,表示方案总数。
数据范围
1≤N≤20
输入样例:
4
输出样例:
7代码
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int a[30]={1,1,2};
int main()
{
int N;
cin>>N;
for(int i= 3;i<=N;i++)
{
a[i]=a[i-1]+a[i-2]+a[i-3];
}
cout<<a[N];
return 0;
}为什么用递推?
多写几级台阶和对应的方法,i为级数,m=方法数,不难发现
i为0,m=1;
i为1,m=1;
i为2,m=2;
i为3,m=4;
i为4,m=7;
i为5,m=13;推出规律 第i级台阶到达的方法数位前三层方法数之和,代码体现如下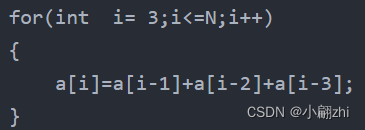
文章来源:https://blog.csdn.net/m0_62793538/article/details/135256789
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- SIT3491ISO具有隔离功能,256 节点,全双工 RS422/RS485 芯片
- 自然语言处理1——探索自然语言处理的基础 - Python入门篇
- 【算法题】2. 两数相加
- Docker网络
- 腾讯云发送短信接口
- uniapp+vue3打包问题记录
- RK3568平台 PWM Backlight控制背光亮度
- YOLOv5:指定类别进行评估验证
- POI-tl 知识整理:整理4 自定义渲染策略生成动态表格
- GrayLog日志平台的基本使用-Windows日志接入