数据结构之堆——学习笔记

1.堆的简介：

?

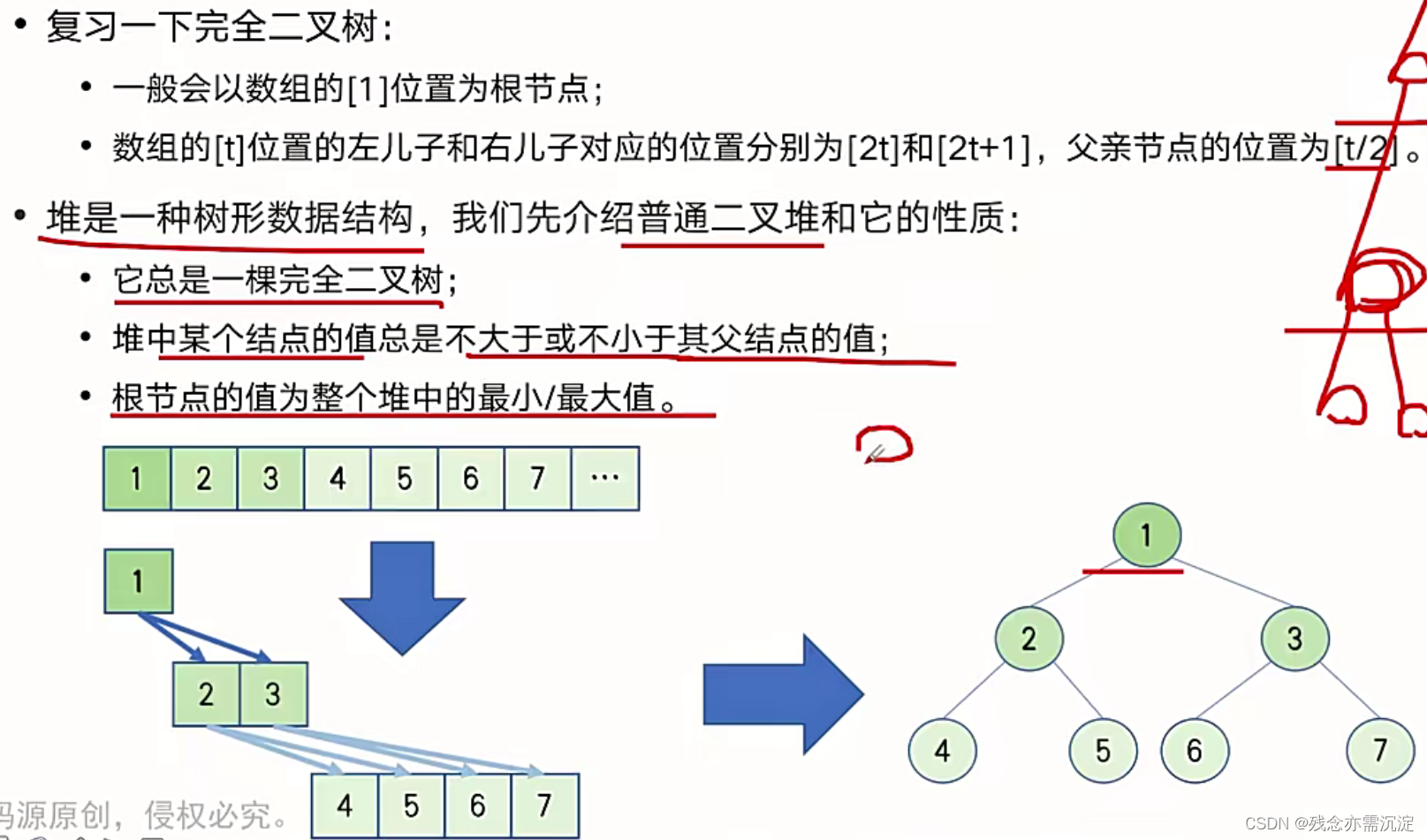
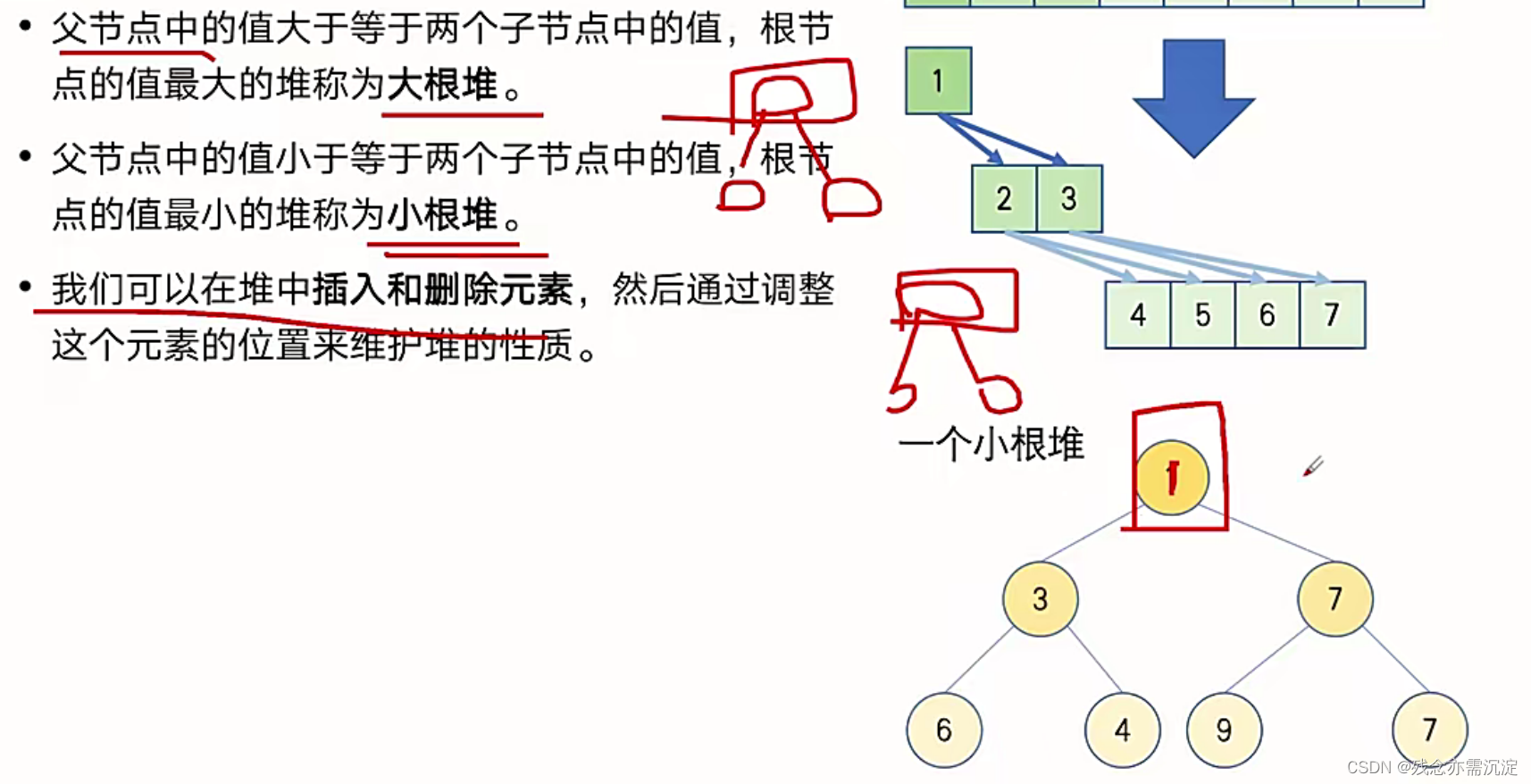接下来看一下堆的建立；

?

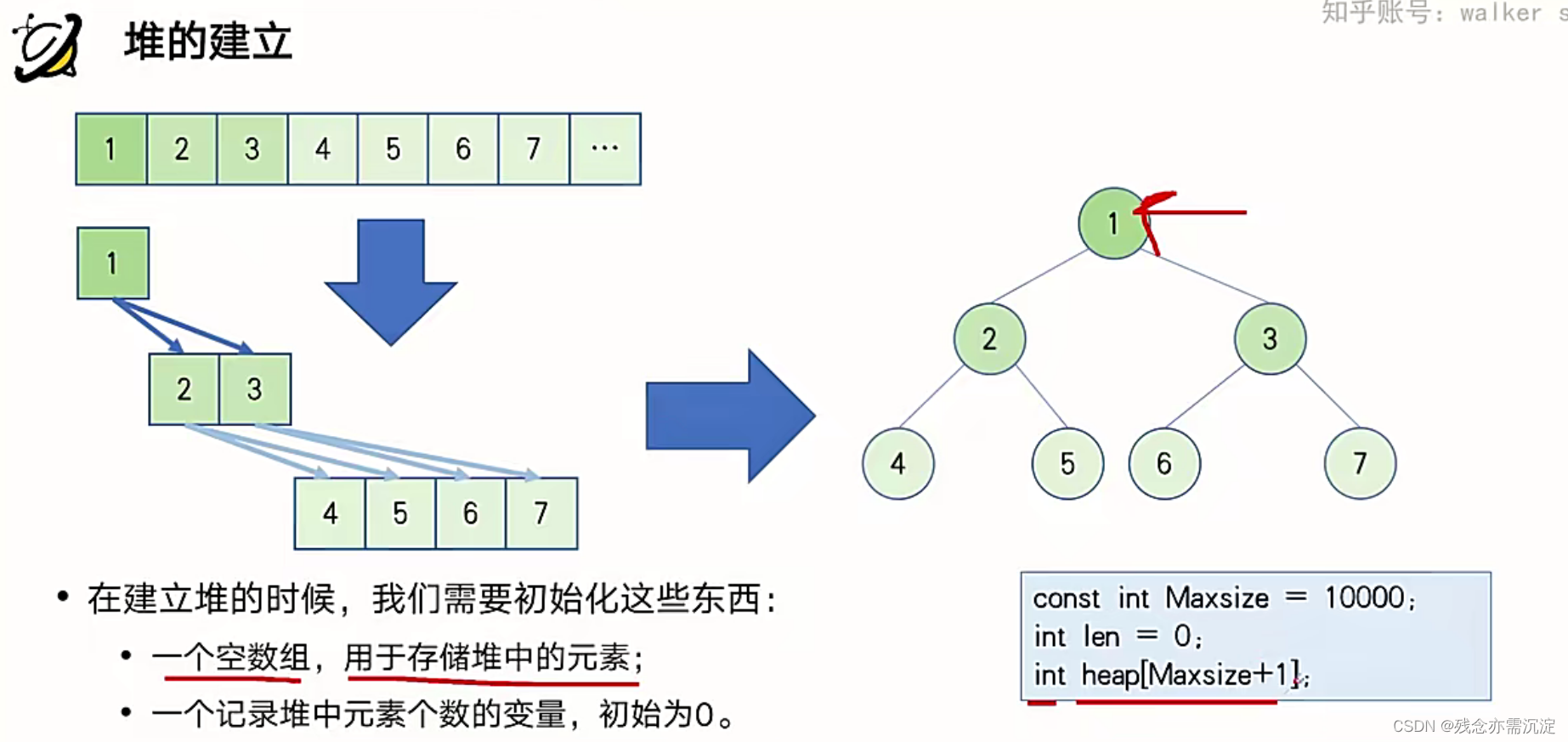接下来是如何在堆中插入数据以及删除数据：

?

?

?

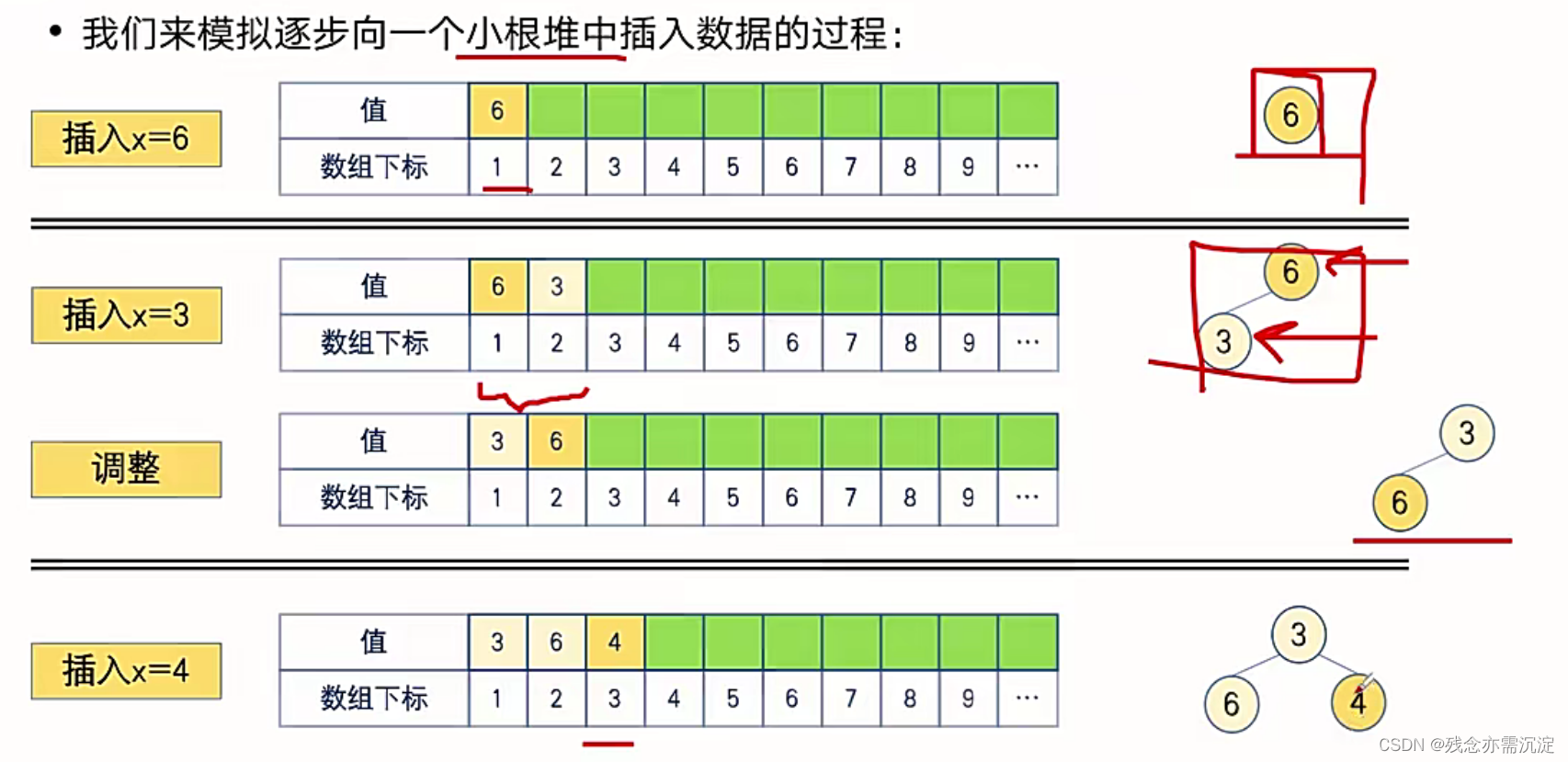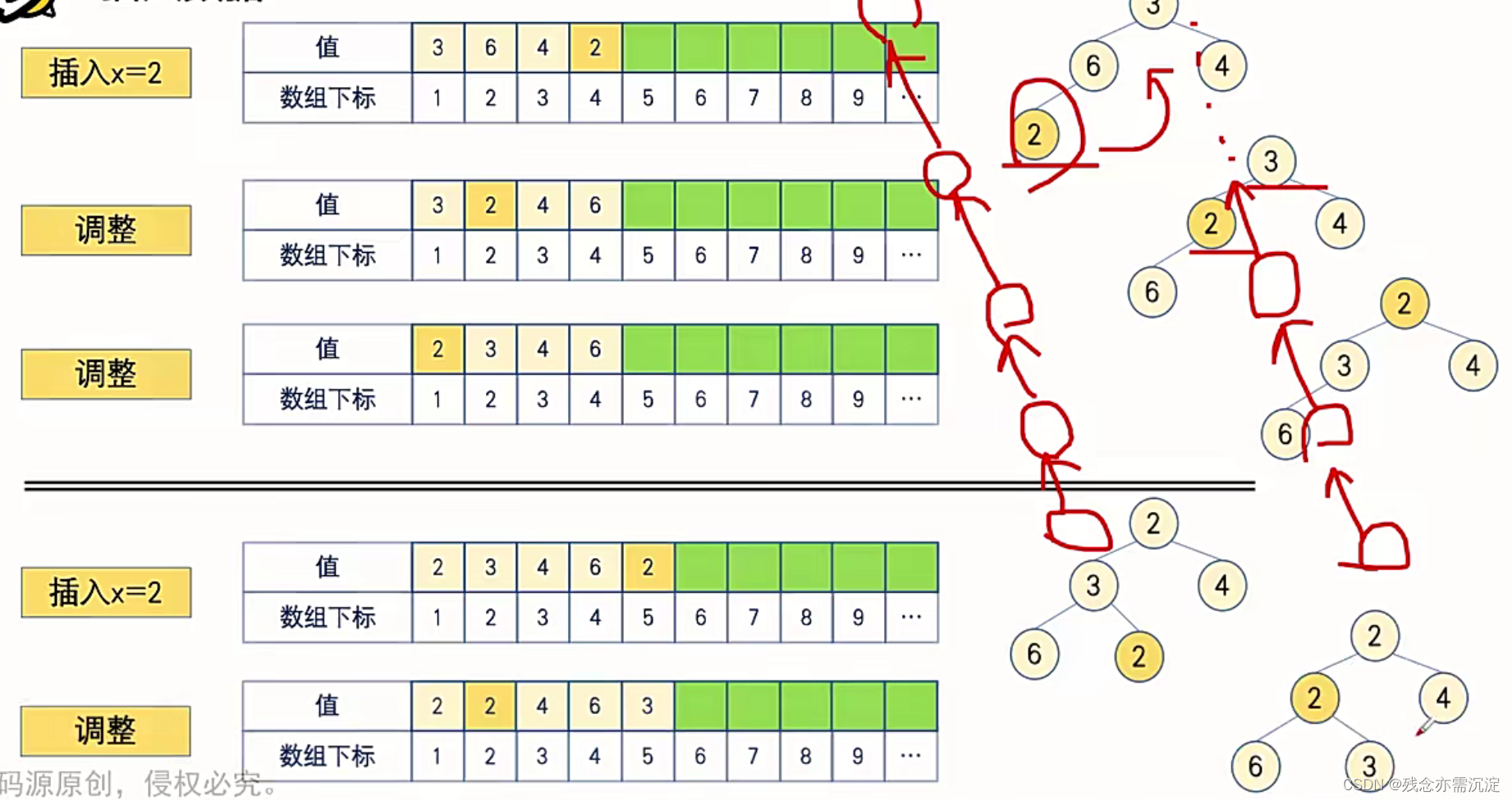
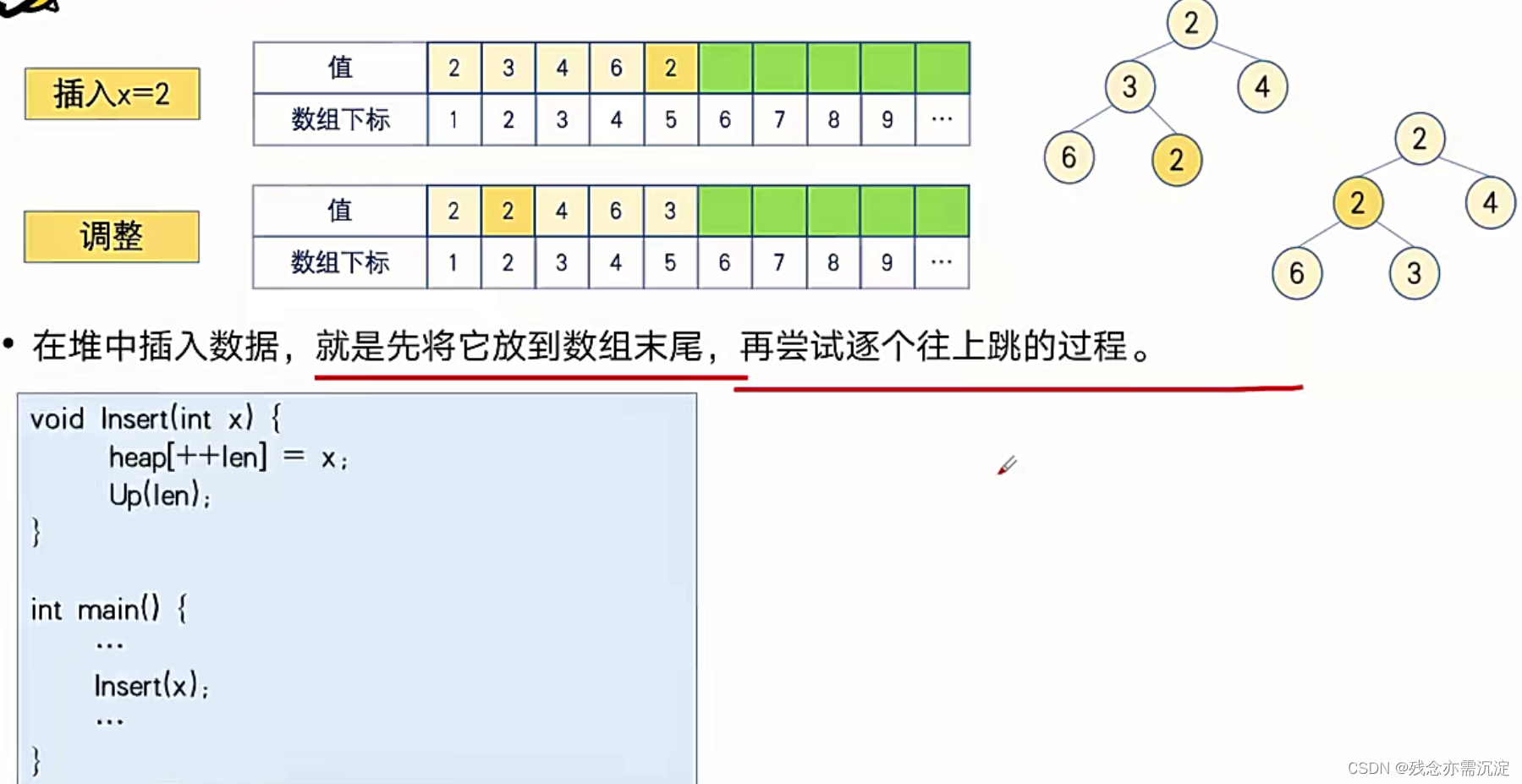大根堆的插入操作类似只是改变了一下大于和小于符号，同时插入操作的时间复杂度为O（logn）。

?

?

?

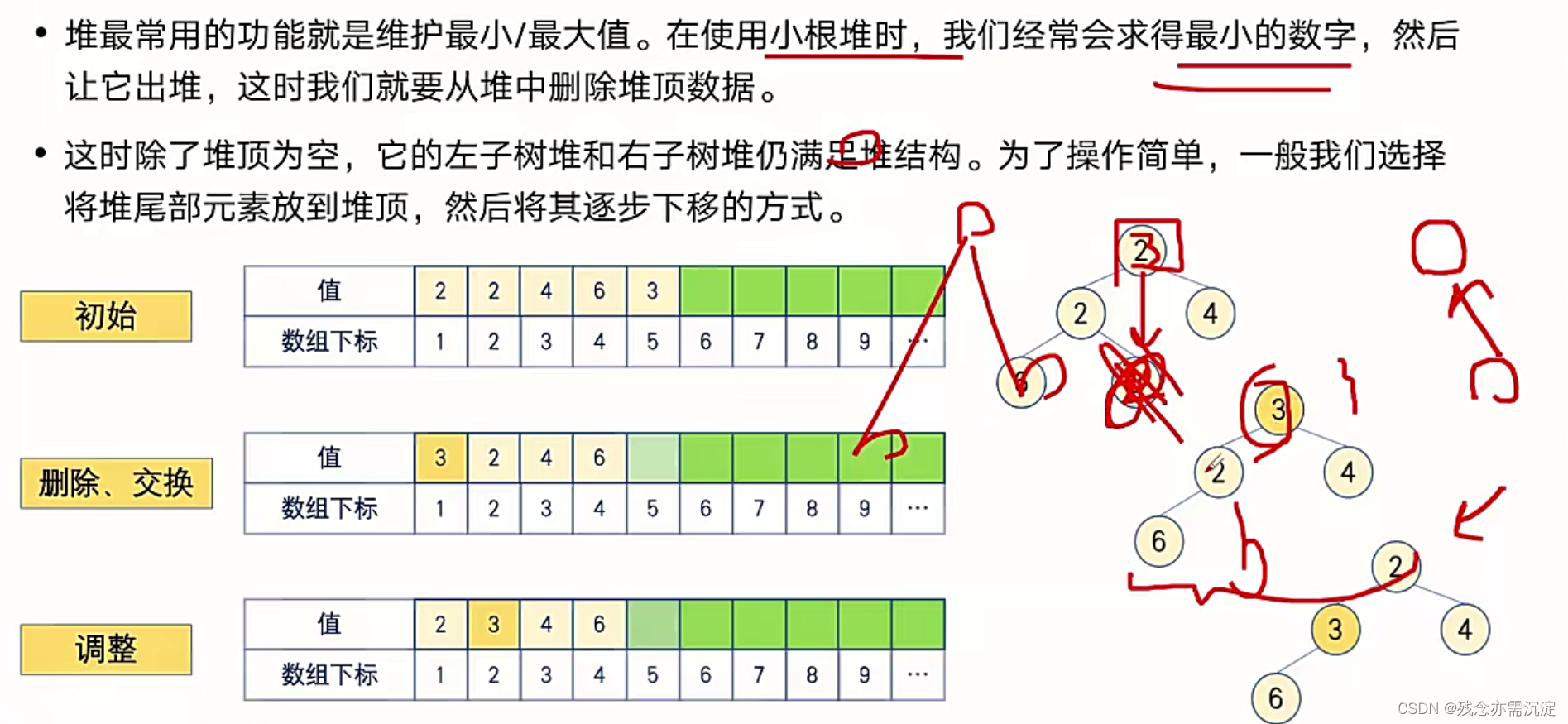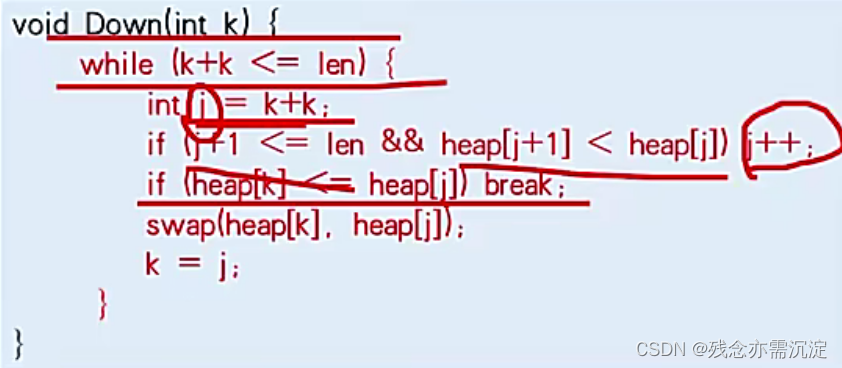?来看几个问题：

答案当然是不可以：

?

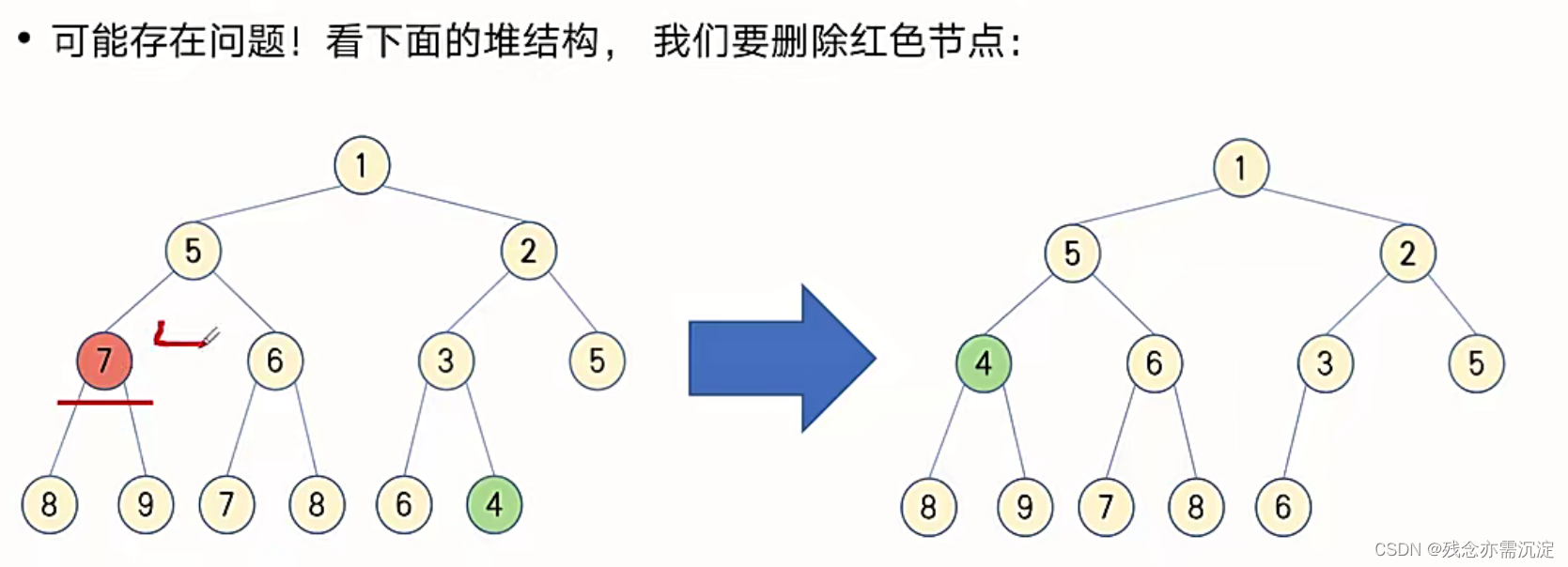这样的话就能根据原堆的末尾数字的大小来判断是应该尝试将它往上还是下进行移动。

?来看看STL里面的优先队列：

?

?

?值得注意的是 用优先队列是没有clear操作的。

接下来看几道例题：

1.堆排序：

?

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+100;
int n,heap[N],x,len=0;
inline void up(int x){
	while(x>1 && heap[x]<heap[x/2]){
	swap(heap[x],heap[x/2]);
	x/=2;
	}
}
inline void down(int k){
	while(k+k<=len){
		int j=k+k;
		if(j+1<=len && heap[j+1]<heap[j]) ++j;
		if(heap[j]>=heap[k]) break;
		swap(heap[k],heap[j]);
		k=j;
	}
} 
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>x;
		heap[++len]=x;
		up(len);
	}
	for(int i=1;i<=n;i++){
		cout<<heap[1]<<' ';
		swap(heap[1],heap[len]);
		--len;
		down(1);
	}
	return 0;
}

事实上用优先队列来做会非常的简单：

#include<bits/stdc++.h>
using namespace std;
priority_queue<int,vector<int>,greater<int>>q;
const int N=1e5+100;
int n;
/*inline void up(int x){
	while(x>1 && heap[x]<=heap[x/2]){
		swap(heap[x],heap[x/2]);
		x/=2;
	}
}
inline void down(int x){
	while(x+x<=len){
		int y=x+x;
		if(y+1<=len && heap[y+1]<heap[y])  ++y;
		if(heap[y]>=heap[x]) break;
		swap(heap[y],heap[x]);
		x=y;
	}
}*/
int main(){
    cin>>n;
	for(int i=1;i<=n;i++){
		int x;
		cin>>x;
		q.push(x);
	}	
	for(int i=1;i<=n;i++){
		cout<<q.top()<<' ';
		q.pop();
	}
	return 0;
}

使用小根堆的话是需要背一下优先队列的写法，有一点长。

接下来看一下第二题：

合并数列：

?这道题目的数据范围如果给的很小的话其实可以直接考虑模拟做法，但是实际上这道题目并没有那么的简单，接下来看代码，我在上面给了注释。

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;//这里的N要比序列的个数上限设置的更大
int n,len,m;//n个序列，len代表当前读入的堆的序列的个数，m是最后要输出的数字个数
struct xulie{
	int v,delta;//v代表某一序列当前的堆顶元素，delta代表对应序列的k值
}heap[N];
//对新读入的序列试着将他往上面排的函数
inline void up(int x){
	while(x>1 && heap[x].v<=heap[x/2].v){
		swap(heap[x],heap[x/2]);
		x/=2;
	}
}
//将堆首的元素试着往下排
inline void down(int x){
	while(x+x<=len){
		int y=x+x;
		if(y+1<=len && heap[y+1].v<heap[y].v)  ++y;
		if(heap[y].v>=heap[x].v) break;
		swap(heap[y],heap[x]);
		x=y;
	}
}
int main(){
   cin>>n;
   for(int i=1;i<=n;i++){
       int k,b;
       cin>>k>>b;
       heap[++len].v=b;
       heap[len].delta=k;
       up(len);
   }
   cin>>m;
   for(int i=1;i<=m;i++){
   	cout<<heap[1].v<<' ';
   	heap[1].v+=heap[1].delta;
   	//输出堆顶序列这时候的值之后，对该序列的v值加一个delta并将加了之后的堆顶序列试着往下排
   	down(1);
   }
   return 0;
}

这道题的做法还是很有意思的。

接下来看一下第三个题：

大富翁游戏：

?费了九牛二虎之力，可算是搞明白了。。。

代码如下：

#include<bits/stdc++.h>
using namespace std;
struct Info{
	int v,pos;
}heap1[100001],heap2[100001];
int n,m,len1,len2,s1[100001],s2[100001];
inline void up1(int k){
	while(k>1 && heap1[k].v<heap1[k/2].v){
		swap(heap1[k],heap1[k/2]);
		s1[heap1[k].pos]=k;
		s1[heap1[k/2].pos]=k/2;
		k/=2;
	}
}
inline void down1(int k){
	while(k+k<=len1){
		int j=k+k;
		if(j+1<=len1 && heap1[j+1].v<heap1[j].v)
		++j;
		if(heap1[k].v<=heap1[j].v) break;
		swap(heap1[k],heap1[j]);
		s1[heap1[k].pos]=k;
		s1[heap1[j].pos]=j;
		k=j;
	}
}
inline void up2(int k){
	while(k>1 && heap2[k].v>heap2[k/2].v){
		swap(heap2[k],heap2[k/2]);
		s2[heap2[k].pos]=k;
		s2[heap2[k/2].pos]=k/2;
		k/=2;
	}
}
inline void down2(int k){
	while(k+k<=len2){
		int j=k+k;
		if(j+1<=len2 && heap2[j+1].v>heap2[j].v)
		++j;
		if(heap2[k].v>=heap2[j].v) break;
		swap(heap2[k],heap2[j]);
		s2[heap2[k].pos]=k;
		s2[heap2[j].pos]=j;
		k=j;
	}
}
int main(){
	cin>>n;
	len1=len2=0;
	for(int i=1;i<=n;i++){
		heap1[++len1].v=100;
		heap1[len1].pos=i;
		s1[i]=len1;
		up1(len1);
		heap2[++len2].v=100;
		heap2[len2].pos=i;
		s2[i]=len2;
		up2(len2);
	}
	cin>>m;
	for(int i=1;i<=m;i++){
		int x;
		cin>>x;
		if(x==1){
			int y,z;
			cin>>y>>z;
			heap1[s1[y]].v+=z;
			up1(s1[y]);
			down1(s1[y]);
			heap2[s2[y]].v+=z;
			up2(s2[y]);
			down2(s2[y]);
		}
		else{
			cout<<heap2[1].v<<' '<<heap1[1].v<<endl;
		}
	}
	return 0;
}

这里代码中使用了两个堆，heap1 和 heap2，分别用来维护最小堆和最大堆。s1 和 s2 数组用来记录每个人在堆中的位置。代码中的堆结构的使用主要是为了在O(log n)的时间复杂度内找到当前最高和最低资金，以提高效率。在每次资金变动后，通过调整堆，保证堆顶元素分别是当前最小和最大资金。

最后一个题：动态中位数

这里是代码：

#include<bits/stdc++.h>
using namespace std;
int n;
priority_queue<int>a,b;
int main(){
	cin>>n;
	int x;
	cin>>x;
	a.push(x);
	cout<<a.top()<<' ';
	for(int i=1;i<=n/2;i++){
		int x,y,z=a.top();
		cin>>x>>y;
		if(x<z)
		a.push(x);
		else 
		b.push(-x);
		if(y<z)
		a.push(y);
		else 
		b.push(-y);
		if(a.size()-b.size()==3){
			b.push(-a.top());
			a.pop();
		} else 
		if(b.size()-a.size()==1){
			a.push(-b.top());
			b.pop();
		}
		cout<<a.top()<<' ';
	}
	return 0;
}

?

1. priority_queue 的使用：定义了两个优先队列（堆），a 和 b。它们用于存储输入数字，其中 a 是最大堆，b 是最小堆。

2. 第一个数字的处理：从输入中读取第一个数字 x，将其压入最大堆 a 中，然后输出当前中位数（即最大堆的堆顶元素）。

3. 循环处理每个数字对（x，y）：

   • 如果 x 小于当前中位数（即最大堆的堆顶元素 a.top()），则将 x 压入最大堆 a。
   • 否则，将 -x（x 的相反数）压入最小堆 b。
   • 如果 y 小于当前中位数，则将 y 压入最大堆 a。
   • 否则，将 -y（y 的相反数）压入最小堆 b。

4. 调整堆大小：在每次插入后，检查两个堆的大小关系：

   • 如果最大堆 a 的大小比最小堆 b 大 3，将最大堆的堆顶元素弹出并压入最小堆 b。
   • 如果最小堆 b 的大小比最大堆 a 大 1，将最小堆的堆顶元素弹出并取其相反数压入最大堆 a。

5. 输出中位数：每次插入后，输出当前中位数（即最大堆的堆顶元素 a.top()）。

6. 这段代码通过维护最大堆和最小堆，根据输入的数字实时调整堆，以便高效地计算中位数。在中位数的计算过程中，通过在两个堆之间调整元素，确保了两个堆的大小差距在一个合理的范围内。这样做的目的是为了避免在求中位数时需要对所有数据进行排序的开销，从而实现更加高效的中位数计算

希望这一篇学习笔记对读者有所帮助，让我们共同进步。