二叉搜索树第大K节点，剑指offer,力扣

目录

题目地址：

题目：

我们直接看题解吧：

解题方法：

难度分析：

审题目+事例+提示：

解题分析：

解题思路：

代码实现：

代码补充：

代码实现（非递归） ：

---

题目地址：

LCR 174. 寻找二叉搜索树中的目标节点 - 力扣（LeetCode）

难度：简单

今天刷寻找二叉搜索树第大K节点，大家有兴趣可以点上看看题目要求，试着做一下。

题目：

剑指 Offer 54.?二叉搜索树的第k大节点

给定一棵二叉搜索树，请找出其中第?k?大的节点的值。

我们直接看题解吧：

解题方法：

利用递归+中序遍历方法

难度分析：

主要考察二叉搜索树性质与中序遍历特点

审题目+事例+提示：

题目中序列是以二叉搜索树方式存储

解题分析：

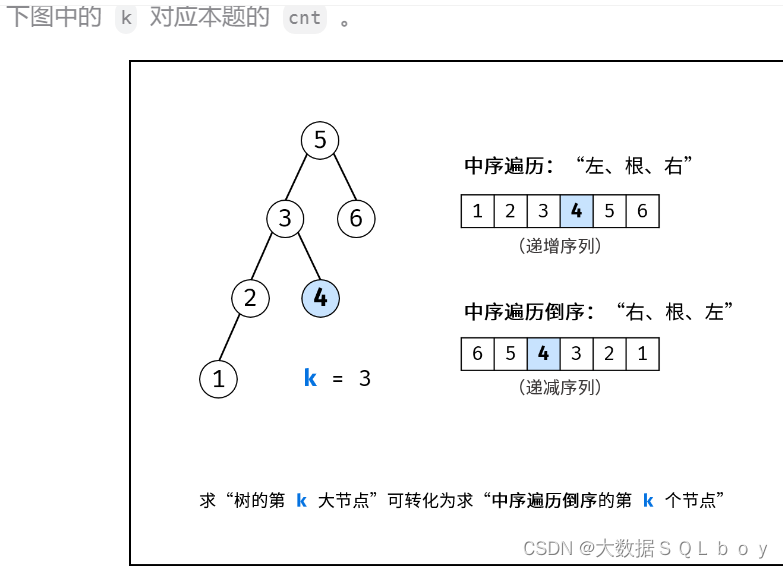
二叉搜索树的中序遍历为?递增序列?，根据此性质，易得二叉搜索树的?中序遍历倒序?为?递减序列?。

因此，求 “二叉搜索树第 cnt大的节点” 可转化为求 “此树的中序遍历倒序的第 cnt个节点”。

中序遍历?为 “左、根、右” 顺序，递归法代码如下：

// 打印中序遍历
void dfs(TreeNode root) {
    if(root == null) return;
    dfs(root.left); // 左
    System.out.println(root.val); // 根
    dfs(root.right); // 右
}

中序遍历的倒序?为 “右、根、左” 顺序，递归法代码如下：

// 打印中序遍历倒序
void dfs(TreeNode root) {
    if(root == null) return;
    dfs(root.right); // 右
    System.out.println(root.val); // 根
    dfs(root.left); // 左
}

参考题解：LCR 174. 寻找二叉搜索树中的目标节点 - 力扣（LeetCode）

解题思路：

为求第 k个节点，需要实现以下 三项工作 ：

? ? ? ·递归遍历时计数，统计当前节点的序号；
? ? ?· 递归到第 cnt?个节点时，应记录结果 res ；
? ? ? ·记录结果后，后续的遍历即失去意义，应提前终止（即返回）。

?递归解析：

? ? ? ?终止条件： 当节点 root 为空（越过叶节点），则直接返回；
? ? ? ?递归右子树： 即 dfs(root.right)；
? ? ? 三项工作：
? ? ? ? ? ? 提前返回： 若 cnt=0，代表已找到目标节点，无需继续遍历，因此直接返回；
? ? ? ? ? ? 统计序号： 执行 cnt=cnt?1 （即从 cnt?减至 0?）；
? ? ? ? ? ? 记录结果： 若 cnt=0，代表当前节点为第 cnt大的节点，因此记录 res=root.val;
? ? ? 递归左子树： 即 dfs(root.left) ；
?

代码实现：

class Solution {
    int res, count;//由于下面形参cnt不能随着dfs的迭代而不断变化，
                 //因此为了记录迭代进程和结果，引入类变量count和res
    public int findTargetNode(TreeNode root, int cnt) {
        count = cnt;//将形参值cnt对类变量count进行初始化
        dfs(root);//这里不需要引入形参cnt，dfs中直接使用的是初始值为cnt的类变量count
        return res;
    }
    void dfs(TreeNode root) {
        if(root == null) return;//当root为空，终止递归
        dfs(root.right);
        if(cnt == 0) return;//当count=0即找到目标res，终止递归
        if(--count==0){//先--，再判断
            res = root.val;
            return;//这里的return可以避免之后的无效迭代dfs(root.left);
        }
        dfs(root.left);
    }
}

代码补充：

1、

题目指出：1≤cnt≤N（二叉搜索树节点个数）；因此无需考虑 cnt>Nc 的情况。
若考虑，可以在中序遍历完成后判断 cnt>0 是否成立，若成立则说明 cnt>N 。

2、

count==0的判断条件是否可以并到第一个if(root==null)中？

count==0得放在--count之前才有效，回溯的过程可能会继续--，导致count<0，并没有起到剪枝效果，打印下count的值你就发现了

代码实现（非递归） ：

class Solution { 
    public int findTargetNode(TreeNode root, int cnt) {
          // reverse-inorder （逆向中序排序 找到需要的第cut个就好了）
        LinkedList<TreeNode> stack = new LinkedList<>();
        TreeNode node = root;
        int count = 0;
        while(node != null || !stack.isEmpty()){
            if (node != null){
                stack.push(node);
                node = node.right;
            }else{
                // 说明是空了向左边走
                TreeNode pop = stack.pop();
                count++;
                if(count == cnt){
                    return pop.val;
                }
                node = pop.left;
            }
        }
        // 这里其实是没有必要的 但是必须要返回值
        return -1;
    }
}