假设检验(超详细)
假设检验
什么是假设检验
假设检验( hypothesis testing)是指从对总体参数所做的一个假设开始,然后搜集样本数据,计算出样本统计量,进而运用这些数据测定假设的总体参数在多大程度上是可靠的,并做出承认还是拒绝该假设的判断。
为什么要用假设检验
我们在生活中经常会遇到对一个总体数据进行评估的问题,但我们又不能直接统计全部数据,这时就需要从总体中抽出一部分样本,用样本来估计总体情况。这时候就可以用到假设检验,它可以有助于评估出现正确结果的可能性。
假设检验的定义和原理
定义:假设检验是先对总体参数提出一个假设值,然后利用样本信息判断这一假设是否成立。
原理:小概率原理即小概率事件在一次抽样中不发生。
由定义可知,我们需要对结果进行假设,然后拿样本数据去验证这个假设。
所以做假设检验时会设置两个假设:
一种叫原假设,也叫零假设,用H0表示。【希望原假设被接受】
另外一种叫备择假设,用H1表示。【与原假设对立】
接受H0与拒绝H0的方法:看小概率事件是否发生。
假设检验步骤
1先假设H0是真的,然后判别小概率事件是否发生,如果发生,就拒绝H0,接受H1,如果没有发生,就接受H0。解释:整体的思想为小概率事件在一次抽样中不发生,小概率事件不发生是极大概率事件,所以上面的假设就是合理的。
2深入思考,如果小概率事件发生了,此时却拒绝了H0,就是拒绝了真实的情况,那么就犯了第一类错误,即拒真;拒真的概率就是我们所定的α,即显著性水平,一般为0.05。
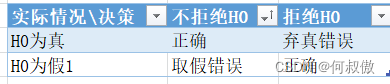
第一类错误:P(拒绝H0|H0真)=α
第二类错误:P(接受HO|H0假)=β
F检验与T检验
F检验【线性关系检验】
目的:
检验自变量x与因变量y之间的线性关系是否显著,或者说,他们之间能否用一个线性模型来表示。【对于整个方程显著性的检验】
T检验【回归系数检验】
目的:
通过对回归系数β与0的检验,看其是否有显著性差异,来判断回归系数是否显著。【检验系数是否显著】
代码解读
广告投入与销售额是否符合线性回归模型
import pandas as pd
data = pd.read_csv("data.csv")
x = data[['广告投入']]
y = data[['销售额']]
这是所需要的数据
data,csv
因为要使用T检验和F检验,所以我们要新添加一个库
import statsmodels.api as sm
y=x0β0+x1β1因为在statsmodels库中x0的值不会自动填充为1所以要加上
X = sm.add_constant(x)
用最小二乘法计算出X,y的值从而得到系数
model = sm.OLS(y, X)
result = model.fit()
params = result.params
汇总结果,观察T检验与F检验的值是否符合要求
print(result.summary())
这是得到的结果
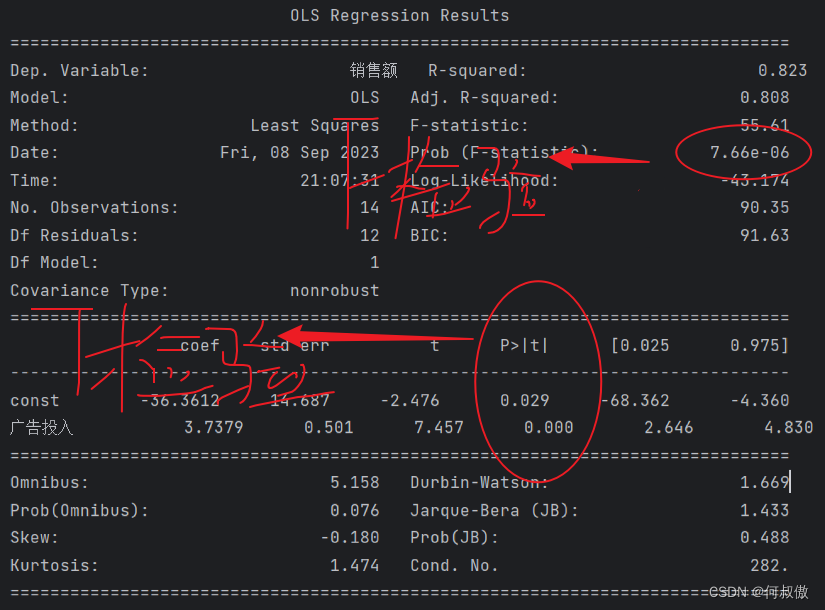
观察可得T检验和F检验都符合,其值均小于0.05,符合结果。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 二叉树的基本操作
- K8s 源码剖析及debug实战(一):Minikube 安装及源码准备
- MongoDB
- vue使用elementui 的 table且自定义某列表头时,添加的点击事件和自带的筛选功能有类似冒泡行为
- 怎样存值以及取值
- 一文读懂 $mash 通证 “Fair Launch” 规则(幸运池玩法解读篇)
- vue3通过ref调用子组件方法,第一次点击报找不到该方法,ref和v-if冲突
- 企业公众号如何排版,排版技巧分享
- Java不使用框架,简单使用JDBC封装MySQL连接【新手向】
- 深陷制裁风波后,禾赛科技激光雷达再创新纪录 | 百能云芯