图分割算法之贪心算法
发布时间:2023年12月28日
1 贪心算法的思想
????????Linear Deterministic Greedy partitioning (LDG)考虑在分割的时候将邻居结点放置在一起,以减少切割边。它采用贪心算法将一个结点放置在包含其邻居最多的子图中,同时保证每个子图的结点负载均衡,整个算法流程图如下 其中 C 表示每个分区的期望值,w(i)? 表示当前子图在平衡状态下剩余容量,g(v,Pi)? 表示再考虑负载的情况下结点 v 和子图 Pi 中结点邻居个数的交集,该打分函数作为将结点 v 分配到最大分数的子图中
其中 C 表示每个分区的期望值,w(i)? 表示当前子图在平衡状态下剩余容量,g(v,Pi)? 表示再考虑负载的情况下结点 v 和子图 Pi 中结点邻居个数的交集,该打分函数作为将结点 v 分配到最大分数的子图中
2 代码设计
父类设计Partitioner
#ifndef PARTITION_H
#define PARTITION_H
#include <vector>
#include <algorithm>
#include <numeric>
#include <random>
class Partitioner
{
public:
/// <summary>
/// 图分区的构造函数
/// </summary>
/// <param name="adjMatrix_">临界矩阵</param>
Partitioner(std::vector<std::vector<int>> adjMatrix_);
/// <summary>
/// 图分割算法
/// </summary>
/// <param name="partNums">分区个数</param>
virtual void execute(int partNums) = 0;
/// <summary>
/// 评估图分割算法
/// </summary>
virtual void evaluate() = 0;
/// <summary>
/// 返回分区结果
/// </summary>
std::vector<int> getResults() const;
/// <summary>
/// 获取顶点总数
/// </summary>
int getNumVertics() const;
/// <summary>
/// 获取图的便的总数
/// </summary>
int getNumEdges() const;
private:
protected:
/// <summary>
/// 邻接表存储的图数据
/// </summary>
std::vector<std::vector<int>> adjMatrix;
/// <summary>
/// 分区结果
/// </summary>
std::vector<int> partResults;
int numVertices;
int numEdges;
};
#endif // !PARTITION_H
#include "Partitioner.h"
Partitioner::Partitioner(std::vector<std::vector<int>> adjMatrix_) : adjMatrix(adjMatrix_)
{
numVertices = adjMatrix_.size();
numEdges = 0;
std::for_each(adjMatrix_.begin(), adjMatrix_.end(), [&](const std::vector<int>& edges) {
numEdges += edges.size();
});
}
std::vector<int> Partitioner::getResults() const
{
return partResults;
}
int Partitioner::getNumVertics() const
{
return numVertices;
}
int Partitioner::getNumEdges() const
{
return numEdges;
}
LDGPartitioner的设计
#ifndef LDG_PARTITIONER_H
#define LDG_PARTITIONER_H
#include "Partitioner.h"
#include <unordered_set>
class LDGPartitioner : public Partitioner
{
public:
LDGPartitioner(std::vector<std::vector<int>> adjMatrix_) : Partitioner(adjMatrix_) {};
void execute(int partNums) override;
void evaluate() override;
private:
/// <summary>
/// 计算节点index的邻居和已分配的邻居相交的元素个数
/// </summary>
/// <param name="index">节点的下表</param>
/// <param name="curVec">已分配的邻居</param>
/// <returns></returns>
int intersect(const int index, const std::unordered_set<int>& curVec);
/// <summary>
/// 已分配的集合
/// </summary>
std::vector<std::unordered_set<int>> curParts;
};
#endif // !LDG_PARTITIONER_H
#include "LDGPartitioner.h"
void LDGPartitioner::execute(int partNums)
{
//初始化
std::vector<int> order(numVertices); //节点id的集合
curParts.resize(numVertices);
partResults.resize(numVertices);
// 随机打乱id
std::iota(order.begin(), order.end(), 0);
std::random_shuffle(order.begin(),order.end());
//将前partNums的节点分配给每个分区作为第一个元素
for (int i = 0; i < partNums; i++)
{
curParts[i].insert(order[i]);
partResults[order[i]] = i;
}
// 每个分区的期望值
double expectant = static_cast<double>(numVertices / partNums);
//便利剩余的元素
for (int ii = partNums; ii < numVertices; ii++)
{
//当前节点的id
int vertex = order[ii];
// 每个分区的得分
std::vector<double> scores(partNums, 0);
for (int jj = 0; jj < partNums; jj++)
{
double curSize = curParts[jj].size();
double weight = static_cast<double>(1 - (curSize / expectant));
double neighbors = intersect(vertex, curParts[jj]);
scores[jj] = neighbors * weight;
}
//节点需要分配给得分最高的节点
int maxIndex = std::distance(scores.begin(), std::max_element(scores.begin(), scores.end()));
curParts[maxIndex].insert(vertex);
partResults[vertex] = maxIndex;
}
}
void LDGPartitioner::evaluate()
{
}
int LDGPartitioner::intersect(const int index,const std::unordered_set<int>& curVec)
{
int count = 0;
for (const auto& element : adjMatrix[index])
{
if (curVec.count(element))
count++;
}
return count;
}
主函数测试:
#include <iostream>
#include <vector>
#include <list>
#include <algorithm>
#include <memory>
#include "LDGPartitioner.h"
using namespace std;
// 定义图的邻接表类型
typedef vector<vector<int>> AdjacencyList;
int main() {
// 构造示例图的邻接表
AdjacencyList graph = {
{1, 2, 4},
{0, 2, 4},
{0, 1, 3},
{2, 4},
{0, 1, 3}
};
//Partitioner* ptr = new LDGPartitioner(graph);
unique_ptr<Partitioner> ptr = make_unique<LDGPartitioner>(graph);
ptr->execute(3);
// 初始化划分
vector<int> partition = ptr->getResults();
// 输出划分结果
for (int i = 0; i < partition.size(); i++) {
cout << "Vertex " << i << " belongs to Partition " << partition[i] << endl;
}
return 0;
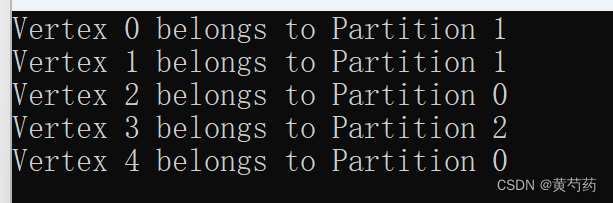
}3 执行结果
????????
文章来源:https://blog.csdn.net/qq_39591612/article/details/135277788
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 第八章[字符串]:8.2:字符串format()函数
- Day30 78子集 90子集II 491非递减子序列
- 设计模式之-3种常见的工厂模式简单工厂模式、工厂方法模式和抽象工厂模式,每一种模式的概念、使用场景和优缺点。
- DolphinDB 高可用集群迁移指南
- element-ui组件DatePicker日期选择器移动端兼容
- livox avia平台搭建
- 毅速:一文说清3D打印随形水路的优势
- 浅谈 ST 表
- Hive02_基本使用,常用命令
- 基于mt19937_64的字符串哈希(板子整理)