【算法】队列+bfs算法 解决树的相关算法题（C++）

1. 前言

队列 与 宽度优先算法（BFS）是解决很多算法问题的常见工具。

BFS通过逐层遍历图或树的节点来寻找解决问题的最短路径或最短步骤。使用队列可以很好地支持BFS算法的实现。

下面是一个使用队列和宽度优先算法解决问题的一般步骤：

1. 创建一个空队列，并将起始节点放入队列中。
2. 创建一个集合用于记录已经访问过的节点，防止重复访问。(visited数组，一般用于路径、迷宫问题)
3. 初始化其他必要的辅助数据结构，例如距离数组或状态数组等。
4. 开始循环，直到队列为空：
   • 从队列中取出一个节点作为当前节点。
   • 如果当前节点是目标节点，说明找到了解，结束搜索。
   • 否则，将当前节点的所有未访问过的邻居节点加入队列，并将这些节点标记为已访问。
5. 如果需要记录路径或其他信息，可以在搜索过程中相应地更新辅助数据结构。
6. 如果队列为空，说明不存在解。

使用队列和宽度优先算法可以解决许多问题，例如迷宫问题、最短路径问题、连通性问题等。具体的实现方式可能因问题而异，但基本思路是相似的。

---

2. 算法题

429.N叉树的层序遍历

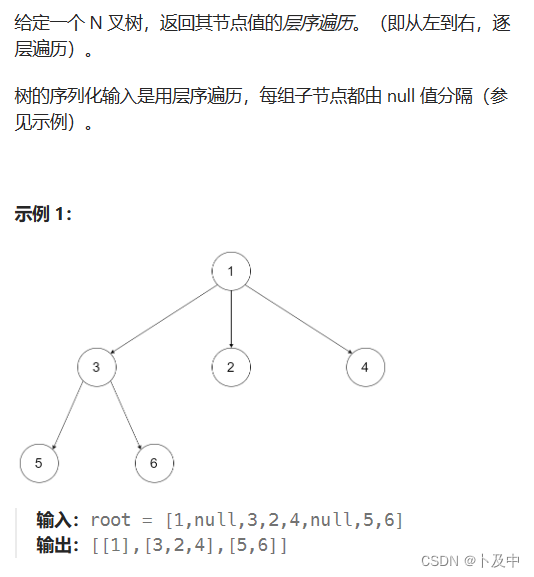
思路

• 解法：队列，宽度优先搜索
  

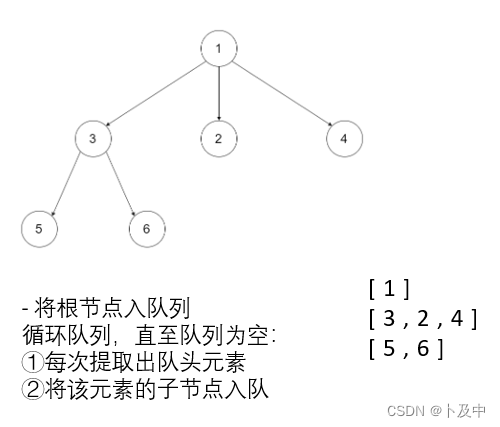
  1. 如上图所写，首先将根节点入队
  2. 循环队列，直至队列为空：
     3. q.size即为该层节点数，循环q.size次：提取出队头节点，并将该节点的所有子节点入队
  3. 每遍历一层，将结果加入到结果数组ret中

代码

vector<vector<int>> levelOrder(Node* root) {
    vector<vector<int>> ret; // 最终结果
    queue<Node*> q; // 用队列记录节点
    // 将本层元素放入队列，提取出值后出队，将子节点入队
    if(root) q.push(root);
    else    return ret;
    while(q.size())
    {
        int sz = q.size(); // 记录本层元素个数
        vector<int> tmp; // 用于存储本层元素值
        for(int i = 0; i < sz; ++i)
        {
            Node* t = q.front();
            q.pop();
            tmp.push_back(t->val); // tmp记录该层节点值
            for(Node* child : t->children) // 当前节点的子节点入队
            {
                if(child) // 不为空
                    q.push(child);
            }
        }
        ret.push_back(tmp); // 更新结果
    }
    return ret;
}

---

103.二叉树的锯齿形层序遍历

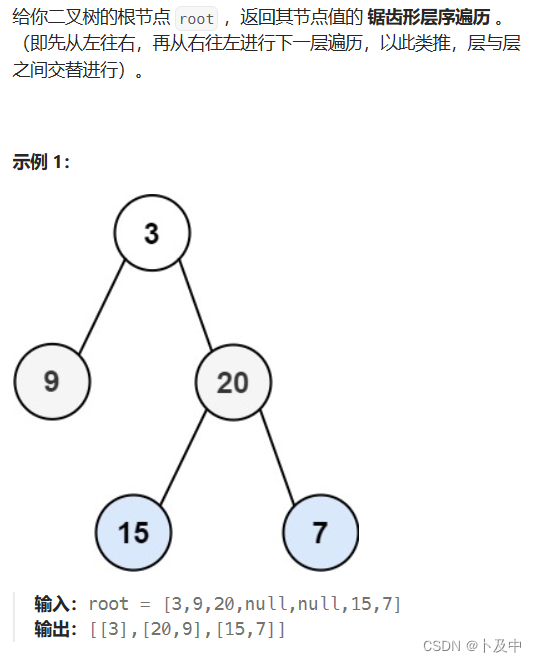
思路

• 题意分析：要求按照先从左往右进行一层遍历、再从左往右进行下一层遍历，重复遍历完二叉树
  • 我们可以将其理解为奇数层正序遍历（从左向右），偶数层逆序遍历
• 解法：队列，宽度优先搜索
• 该题与上一道很类似，只需要添加一个遍历用于标记当前层为奇数还是偶数，用于判断逆序还是正序
  1. 使用一个队列来存储当前层的所有节点，同时记录当前层的节点数。
  2. 依次从队列中取出节点，将其值加入到当前层的结果集tmp中，并将其左右子节点加入队列中。
  3. 如果当前层为偶数层，则需要将tmp逆序后再加入到结果集ret中。
  4. 最后返回结果集ret。

代码

vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
    // 锯齿形层序遍历：偶数层逆序遍历，奇数层正常遍历
    vector<vector<int>> ret;
    queue<TreeNode*> q;
    if(!root) return ret;
    else q.push(root);
    int level = 1; // 根据flag判断是否逆序
    while(q.size())
    {
        int sz = q.size(); // 记录本层个数
        vector<int> tmp;
        for(int i = 0; i < sz; ++i)
        {
            TreeNode* t = q.front();
            q.pop();
            tmp.push_back(t->val);
            if(t->left) q.push(t->left);
            if(t->right) q.push(t->right);
        }
        if(level % 2 == 0)   reverse(tmp.begin(), tmp.end());
        ret.push_back(tmp);
        ++level;
    }
    
    return ret;
}

---

662.二叉树最大宽度

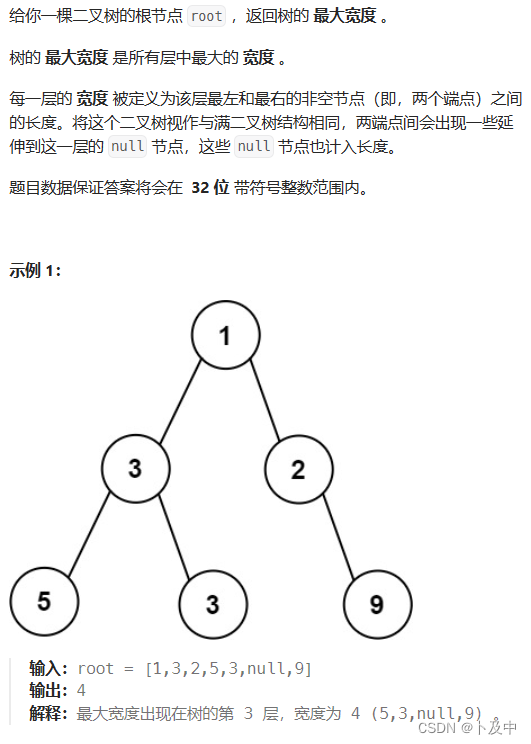
思路

• 题意分析：即返回二叉树的最大宽度，即最大层的宽度
• 解法：记录节点下标、数组表示队列
  
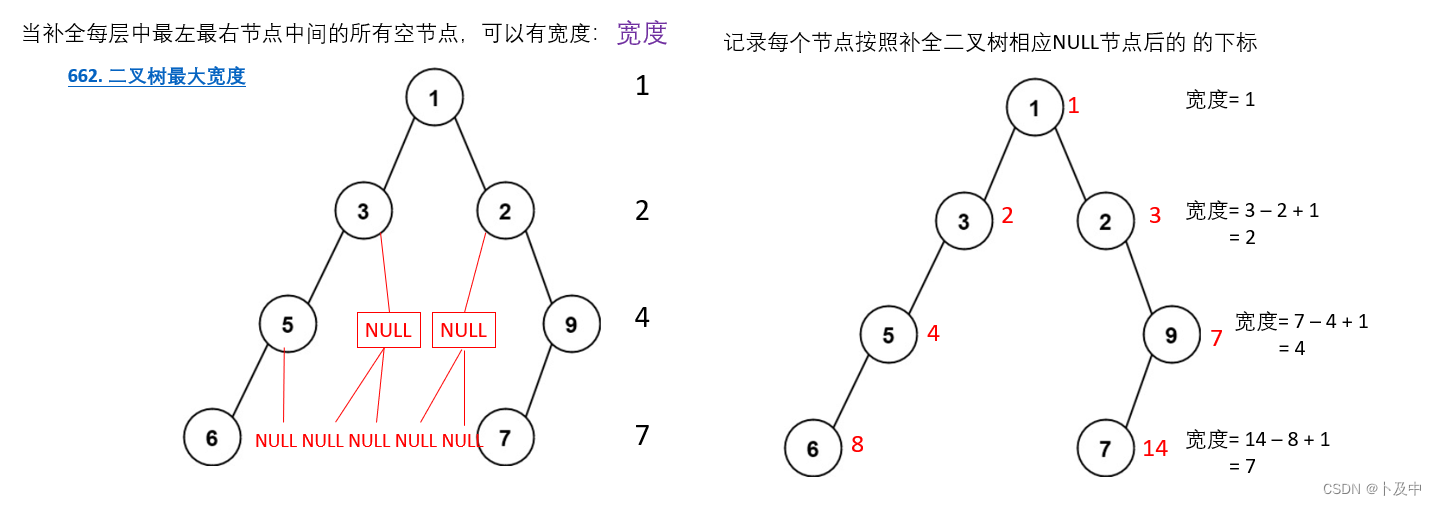
  • 如上图的思路，我们用数组表示队列，队列中存放pair类型，分别为节点和其对应的下标
  1. 将根节点及其下标1插入队列，进行循环，直至队列为空
  2. 提取队尾和队头两元素（即为该层的最左最有的节点）并记录 / 更新结果
  3. 将该层的所有子节点入队
  4. 最后返回结果ret

代码

int widthOfBinaryTree(TreeNode* root) {
    // 队列（数组）存储节点及其下标（补全null节点后的下标）
    vector<pair<TreeNode*, unsigned int>> q;
    // q.push_back(make_pair<nullptr, 0>); 
    if(!root) return 0;
    else q.push_back({root, 1}); // // 根节点从1下标开始
    unsigned int ret = 0; // 最终结果

    while(q.size())
    {
        // 计算本层宽度
        auto [node1, x1] = q[0]; // 提取一个pair类型
        auto [node2, x2] = q.back();
        ret = max(ret, x2 - x1 + 1);

        vector<pair<TreeNode*, unsigned int>> tmp; // tmp存储下一层节点信息，覆盖q
        for(auto& [node, x] : q)
        {
            // 左孩子下标：2x 右孩子下标:2x+1
            if(node->left) tmp.push_back({node->left, 2*x});
            if(node->right) tmp.push_back({node->right, 2*x + 1});
        }

        q = tmp;
    }
    return ret;
}

---

515.在每个树行中找最大值

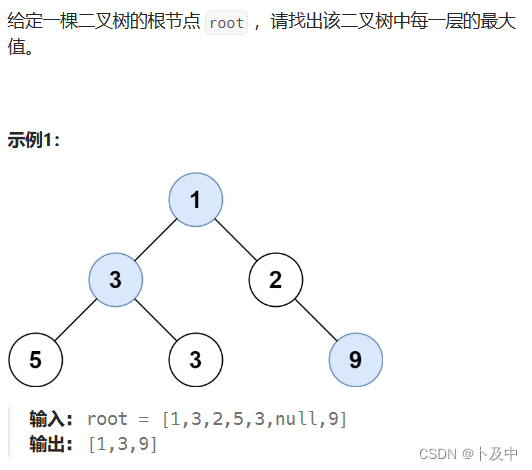
思路

• 解法：队列 + 层序遍历
• 直接利用队列队树进行层序遍历即可
• 每层循环定义一次变量maxVal用于寻找最大值

代码

vector<int> largestValues(TreeNode* root) {
    vector<int> ret; // 结果数组
    queue<TreeNode*> q; // 队列用于层序遍历
    if(!root) return ret;
    else q.push(root);
    
    while(!q.empty())
    {
        int sz = q.size();
        int maxVal = INT_MIN; // 用于比较节点大小 
        while(sz--)
        {
            auto t = q.front(); // 提取当前节点
            q.pop();
            maxVal = max(maxVal, t->val);
            if(t->left) q.push(t->left);
            if(t->right) q.push(t->right);
        }
        ret.push_back(maxVal);
    }

    return ret;
}