【模式识别】探秘聚类奥秘：K-均值聚类算法解密与实战
?🌈个人主页：Sarapines Programmer
🔥?系列专栏：《模式之谜 | 数据奇迹解码》
?诗赋清音：云生高巅梦远游， 星光点缀碧海愁。 山川深邃情难晤， 剑气凌云志自修。
目录
🌌1 初识模式识别
模式识别是一种通过对数据进行分析和学习，从中提取模式并做出决策的技术。这一领域涵盖了多种技术和方法，可用于处理各种类型的数据，包括图像、语音、文本等。以下是一些常见的模式识别技术：
图像识别：
计算机视觉：使用计算机和算法模拟人类视觉，使机器能够理解和解释图像内容。常见的应用包括人脸识别、物体检测、图像分类等。
卷积神经网络（CNN）：一种专门用于图像识别的深度学习模型，通过卷积层、池化层等结构提取图像中的特征。
语音识别：
自然语言处理（NLP）：涉及对人类语言进行处理和理解的技术。包括文本分析、情感分析、命名实体识别等。
语音识别：将语音信号转换为文本，使机器能够理解和处理语音命令。常见应用包括语音助手和语音搜索。
模式识别在生物医学领域的应用：
生物特征识别：包括指纹识别、虹膜识别、基因序列分析等，用于生物医学研究和安全身份验证。
医学图像分析：利用模式识别技术分析医学影像，如MRI、CT扫描等，以辅助医生进行诊断。
时间序列分析：
- 时间序列模式识别：对时间序列数据进行建模和分析，用于预测趋势、检测异常等。在金融、气象、股票市场等领域有广泛应用。
数据挖掘和机器学习：
聚类算法：将数据集中的相似对象分组，常用于无监督学习，如K均值聚类。
分类算法：建立模型来对数据进行分类，如决策树、支持向量机等。
回归分析：用于建立输入和输出之间的关系，用于预测数值型结果。
深度学习：通过多层神经网络学习数据的表示，适用于处理大规模和复杂的数据。
模式识别在安全领域的应用：
行为分析：监测和识别异常行为，如入侵检测系统。
生物特征识别：用于身份验证和访问控制，如指纹、面部识别。
这些技术通常不是孤立存在的，而是相互交叉和融合的，以解决更复杂的问题。在实际应用中，根据具体的问题和数据特点选择合适的模式识别技术是至关重要的。
🌌2?K-均值聚类
🌍2.1 研究目的
- 理解K-均值聚类算法的核心原理，包括初始化、数据点分配和聚类中心更新。
- 掌握在Visual Studio Code中使用C++实现K-均值聚类算法的基本技能，包括项目搭建、数据处理和算法实现。
- 通过选择挑战性数据集，实际应用K-均值聚类算法并分析不同K值对聚类效果的影响，以及聚类结果的可视化展示。
🌍2.2?研究环境
-
C++编程语言及其相关库：
- 语言支持： VSCode具备强大的C++语言支持，提供代码高亮、自动完成等功能，使得编码更加高效。
- Eigen库： 作为线性代数的重要工具，Eigen库被集成用于进行高效的线性代数运算，为数学计算提供了强大的支持。
-
OpenCV库：
- 图像处理： OpenCV库作为计算机视觉领域的重要工具，为图像处理和可视化提供了广泛的功能。包括图像读取、处理、特征提取等一系列操作，为图像相关的应用提供了基础支持。
- 可视化： OpenCV还支持直观的图像可视化，使开发者能够直观地观察图像处理的效果，有助于调试和优化。
-
C++编译器配置：
- GCC配置： 在使用VSCode进行C++开发时，确保已配置好C++编译器，常用的是GNU Compiler Collection（GCC）。正确的配置保证了代码的正确编译和执行。
-
硬件环境：
- 计算资源： 为了处理图像数据，需要充足的计算资源，包括足够的内存和强大的CPU/GPU。这保障了对大规模图像数据进行高效处理和运算。
- 内存管理： 在处理大规模图像数据时，合理的内存管理变得至关重要，以防止内存溢出和提高程序运行效率。
🌍2.3?研究内容
🌕2.3.1 算法原理介绍
K-均值聚类（K-means）是一种常用的无监督学习算法，用于将数据集中的样本分成K个不同的类别或簇。其主要目标是通过最小化簇内样本的方差来实现数据的分组。
以下是K-均值聚类的算法原理：
初始化： 首先，选择K个初始的聚类中心，这些中心可以是随机选择的数据点，或者通过其他方法得到。这些中心将作为簇的代表。
分配数据点： 对于每个数据点，将其分配到距离最近的聚类中心所属的簇。这里通常使用欧氏距离来度量数据点与聚类中心之间的距离。
更新聚类中心： 对于每个簇，计算其中所有数据点的平均值，将该平均值作为新的聚类中心。这一步相当于重新调整簇的位置，以使得簇内样本的方差最小化。
重复迭代： 重复步骤2和步骤3，直到满足停止条件。停止条件可以是达到预定的迭代次数，或者当聚类中心的变化很小时，即收敛到稳定的簇分配。
整个过程可以总结为以下步骤：
- 初始化： 选择K个初始聚类中心。
- 分配： 将每个数据点分配到最近的聚类中心所属的簇。
- 更新： 计算每个簇的新中心，以簇内样本的平均值表示。
- 迭代： 重复分配和更新步骤，直到满足停止条件。
K-均值聚类的优点包括简单易实现、计算效率高，但也有一些缺点，例如对初始聚类中心的选择敏感，对异常值敏感等。在应用K-均值聚类时，通常需要对数据进行标准化，以确保不同特征的尺度不会影响聚类结果。
🌕2.3.2?数据集准备
选择含20个样本的数据集，以便能够明显展示K-均值聚类的效果。
🌕2.3.3?实验步骤
a. 项目搭建： 在VSCODE中创建一个C++项目，配置编译环境，建立项目文件结构。
b. 数据加载与预处理： 读取数据集，进行必要的数据预处理，确保数据格式符合K-均值聚类的要求。
c. 算法实现： 使用C++实现K-均值聚类算法，包括聚类中心初始化、数据点分配、聚类中心更新等关键步骤。
d. 参数调优： 尝试不同的K值，通过评估指标（如簇内平方和）选择最优的K值。
C语言程序：
// c_means.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
#include "math.h"
#define NUM 2
#define NN 20
#define cnum 2
typedef struct {
double x[NUM];
} PATTERN;
PATTERN p[NN]={
//第一题
// {0,0},{1,0},{0,1},{1,1},{2,1},{1,2},{2,2},{3,2},{6,6},{7,6},
// {8,6},{6,7},{7,7},{8,7},{9,7},{7,8},{8,8},{9,8},{8,9},{9,9}
//第二题
// {8,9},{9,9},{0,1},{1,1},{2,1},{1,2},{2,2},{3,2},{6,6},{7,6},
// {8,6},{6,7},{7,7},{8,7},{9,7},{7,8},{8,8},{9,8},{0,0},{1,0}
//第三题
{1,1},{9,9},{1,0},{0,1},{2,1},{1,2},{2,2},{3,2},{6,6},{7,6},
{8,6},{6,7},{7,7},{8,7},{9,7},{7,8},{8,8},{9,8},{8,9},{0,0}
};
PATTERN z[cnum],oldz[cnum];
int nj[cnum];
int cindex[cnum][NN];
double Eucliden(PATTERN x,PATTERN y)
{
int i;
double d;
d=0.0;
for (i=0;i<NUM;i++) {
d+=(x.x[i]-y.x[i])*(x.x[i]-y.x[i]);
}
d=sqrt(d);
return d;
}
bool zequal(PATTERN z1[],PATTERN z2[])
{
int j;
double d;
d=0.0;
for (j=0;j<cnum;j++) {
d+=Eucliden(z1[j],z2[j]);
}
if (d<0.00001) return true;
else return false;
}
void C_mean()
{
int i,j,l;
double d,dmin;
for (j=0;j<cnum;j++) {
z[j]=p[j];
}
do {
for (j=0;j<cnum;j++) {
nj[j]=0;
oldz[j]=z[j];
}
for (i=0;i<NN;i++) {
for (j=0;j<cnum;j++) {
d=Eucliden(z[j],p[i]);
if (j==0) {dmin=d;l=0;}
else {
if (d<dmin) {
dmin=d;
l=j;
}
}
}
cindex[l][nj[l]]=i;
nj[l]++;
}
for (j=0;j<cnum;j++) {
if (nj[j]==0) continue;
for (i=0;i<NUM;i++) {
d=0.0;
for (l=0;l<nj[j];l++) {
d+=p[cindex[j][l]].x[i];
}
d/=nj[j];
z[j].x[i]=d;
}
}
} while (!zequal(z,oldz));
}
void Out_Result()
{
int i,j;
printf("Result: \n");
for (j=0;j<cnum;j++) {
printf("nj[%d]=%d\n",j,nj[j]);
for (i=0;i<nj[j];i++) {
printf("%d,",cindex[j][i]);
}
printf("\n");
}
}
int main(int argc, char* argv[])
{
C_mean();
Out_Result();
return 0;
}程序分析：
这段代码实现了K-均值聚类算法，用于将一组数据点分成两个簇。以下是代码的详细分析：
数据结构定义：
typedef struct { double x[NUM]; } PATTERN;: 定义了一个结构体PATTERN，每个结构体包含一个长度为NUM的数组，用于存储数据点的坐标。
PATTERN p[NN] = {...};: 定义了一个包含NN个数据点的数组p，其中每个数据点的坐标存储在x[NUM]数组中。数据点的数量和坐标是通过修改结构体和数组进行指定的。
PATTERN z[cnum], oldz[cnum];: 定义了两个数组z和oldz，分别用于存储当前聚类中心和上一轮迭代的聚类中心。
int nj[cnum];: 定义了一个整型数组nj，用于存储每个簇的数据点数量。
int cindex[cnum][NN];: 定义了一个二维整型数组cindex，用于存储每个簇的数据点在原始数据集中的索引。距离计算函数：
double Euclidean(PATTERN x, PATTERN y): 计算两个数据点之间的欧氏距离。该函数通过遍历坐标数组计算每个维度上的差值平方和，然后取平方根得到欧氏距离。判断两个聚类中心是否相等的函数：
bool zequal(PATTERN z1[], PATTERN z2[]): 判断两组聚类中心是否相等，通过计算两组中心之间的欧氏距离之和，如果小于一个很小的阈值（0.00001），则认为相等。K-均值聚类算法主体函数：
void C_mean(): 该函数实现了K-均值聚类的主要逻辑。初始化聚类中心，然后通过迭代过程不断更新聚类中心，直到聚类中心不再改变（收敛）为止。结果输出函数：
void Out_Result(): 输出最终的聚类结果，包括每个簇的数据点数量和数据点在原始数据集中的索引。主函数：
int main(int argc, char* argv[]): 主函数调用C_mean()进行聚类，然后调用Out_Result()输出结果。注释：
- 在代码中有三组数据点的注释，分别代表三个不同的数据集。根据需求，你可以选择其中一组数据点集合进行聚类测试。
总体而言，这是一个简单的K-均值聚类实现，适用于二维数据点，可以通过修改
NUM、NN和cnum以及数据点的坐标来适应不同的问题。在实际应用中，可能需要根据具体情况调整算法参数或进行更复杂的扩展。
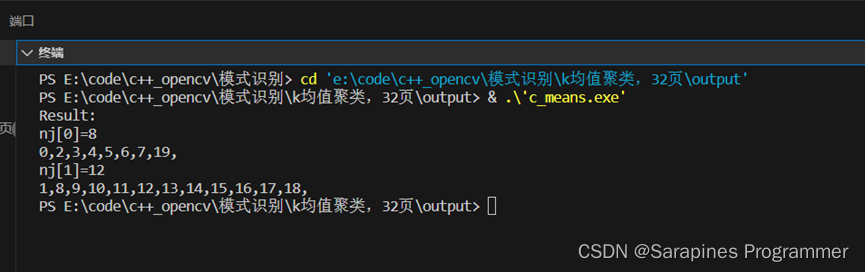
🌕2.3.4?结果分析
输出聚类结果，通过图表展示聚类效果。
🌍2.4?研究体会
-
项目搭建和数据处理：
- 在C++语言的实践中，深入学习了基本结构和语法，掌握了在Visual Studio Code环境下创建C++项目的步骤。
- 对代码组织结构和模块化设计有了更清晰的认识，为后续算法实现提供了基础性支撑。
- 学会使用C++标准库对数据进行加载和预处理，确保数据在K-均值聚类算法中能够被正确处理。
-
算法实现：
- 深入研究了K-均值聚类的核心步骤，包括聚类中心的初始化、数据点的分配和聚类中心的更新。
- 利用C++的强类型特性更好地理解了算法中涉及的数据结构和操作。
- 通过实践提高了编程技能，同时加深了对聚类算法中的数学原理的理解。
-
调优过程和结果分析：
- 意识到K-均值聚类对K值的敏感性，在调优过程中通过尝试不同的K值，更好地理解了聚类数目对算法效果的影响。
- 运用可视化工具直观地了解了聚类效果，对数据点的分布和不同簇之间的关系有了更深刻的认识。
- 这样的深度分析有助于更好地理解数据集的结构和特征，为后续的数据挖掘和分析提供了丰富的信息。
?📝总结
模式匹配领域就像一片未被勘探的信息大海，引领你勇敢踏入数据科学的神秘领域。这是一场独特的学习冒险，从基本概念到算法实现，逐步揭示更深层次的模式分析、匹配算法和智能模式识别的奥秘。渴望挑战模式匹配的学习路径和掌握信息领域的技术？不妨点击下方链接，一同探讨更多数据科学的奇迹吧。我们推出了引领趋势的💻 数据科学专栏：《模式之谜 | 数据奇迹解码》，旨在深度探索模式匹配技术的实际应用和创新。🌐🔍
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Wireshark-win64
- 萨姆·奥尔特曼的预言
- 前段js解决文本框录入保留多位小数设置
- 2024年【G2电站锅炉司炉】考试报名及G2电站锅炉司炉复审考试
- 如何选择合适的4G远程温湿度传感器？
- 资产侦查灯塔系统ARL部署
- Vue以弹窗形式实现导入功能
- 9.1 Maven项目管理（????）
- Python如何操作RabbitMQ实现direct关键字发布订阅模式？有录播直播私教课视频教程
- Linux———ifconfig命令详解