力扣111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。
示例 1：

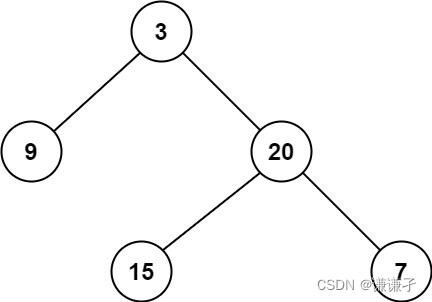
输入：root = [3,9,20,null,null,15,7]
输出：2
示例 2：
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5
提示：
树中节点数的范围在 [0, 105] 内
-1000 <= Node.val <= 1000

方法一：深度优先搜索 思路及解法
首先可以想到使用深度优先搜索的方法，遍历整棵树，记录最小深度。
对于每一个非叶子节点，我们只需要分别计算其左右子树的最小叶子节点深度。这样就将一个大问题转化为了小问题，可以递归地解决该问题。

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }

        if (root.left == null && root.right == null) {
            return 1;
        }

        int min_depth = Integer.MAX_VALUE;
        if (root.left != null) {
            min_depth = Math.min(minDepth(root.left), min_depth);
        }
        if (root.right != null) {
            min_depth = Math.min(minDepth(root.right), min_depth);
        }

        return min_depth + 1;
    }
}

复杂度分析

时间复杂度：O(N)，其中 N 是树的节点数。对每个节点访问一次。

空间复杂度：O(H)，其中 H 是树的高度。空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 O(log?N)。

方法二：广度优先搜索 思路及解法 同样，我们可以想到使用广度优先搜索的方法，遍历整棵树。
当我们找到一个叶子节点时，直接返回这个叶子节点的深度。广度优先搜索的性质保证了最先搜索到的叶子节点的深度一定最小。

class Solution {
    class QueueNode {
        TreeNode node;
        int depth;

        public QueueNode(TreeNode node, int depth) {
            this.node = node;
            this.depth = depth;
        }
    }

    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }

        Queue<QueueNode> queue = new LinkedList<QueueNode>();
        queue.offer(new QueueNode(root, 1));
        while (!queue.isEmpty()) {
            QueueNode nodeDepth = queue.poll();
            TreeNode node = nodeDepth.node;
            int depth = nodeDepth.depth;
            if (node.left == null && node.right == null) {
                return depth;
            }
            if (node.left != null) {
                queue.offer(new QueueNode(node.left, depth + 1));
            }
            if (node.right != null) {
                queue.offer(new QueueNode(node.right, depth + 1));
            }
        }

        return 0;
    }
}