谭浩强【C语言程序设计】第二章习题详解

---

?

目录

?编辑

1，什么是算法？试从日常生活中找3个例子，描述它们的算法。

2，什么叫结构化的算法？为什么要提倡结构化的算法？

3，试述3种基本结构的特点，请另外设计两种基本结构（要符合基本结构的特点）。

4，用传统流程图表示求解以下问题的算法。

（1）有两个瓶子A和B，分别盛放醋和酱油，要求将它们互换。

（2）依次将10个数输入，要求输出其中最大的数。

（3）有3个数a,b,c，要求按大小顺序把它们输出。

（4）求1+2+3+...+100。

（5）判断一个数n能否同时被3和5整除。

（6） 将100~200之间的素数输出

（7）求两个数m和n的最大公约数

（8）求方程ax^2 + bx + c = 0的根。分别考虑：

a.有两个不相等的实根

b.有两个相等的实根?

5.用N-S图表示第4题中各题的算法。

（1）有两个瓶子A和B，分别盛放醋和酱油，要求将它们互换。

（2）依次将10个数输入，要求输出其中最大的数。

（3）有3个数a,b,c，要求按大小顺序把它们输出。

（4）求1+2+3+...+100。

（5）判断一个数n能否同时被3和5整除。

（6） 将100~200之间的素数输出。

（7）求两个数m和n的最大公约数

（8）求方程ax^2 + bx + c = 0的根。分别考虑：

a.有两个不相等的实根

b.有两个相等的实根?

6.用伪代码表示第4题中各题的算法。

（1）有两个瓶子A和B，分别盛放醋和酱油，要求将它们互换。

（2）依次将10个数输入，要求输出其中最大的数。

（3）有3个数a,b,c，要求按大小顺序把它们输出。

（4）求1+2+3+...+100。

（5）判断一个数n能否同时被3和5整除。

（6） 将100~200之间的素数输出。

（7）求两个数m和n的最大公约数

（8）求方程ax^2 + bx + c = 0的根。分别考虑：

a.有两个不相等的实根

b.有两个相等的实根?

7.什么叫结构化程序设计？它的主要内容是什么？

8.用自顶向下，逐步细化的方法进行以下算法的设计：

（1）输出1900 --- 2000年中是闰年的年份，符合下面两个条件之一的年份是闰年。

a、能被4整除但不能被100整除

b、能被100整除且能被400整除

（2）求ax^2 + bx + c = 0的根。分别考虑d = b^2 - 4ac 大于0、等于0和小于0的情况。

（3）输入10个数，输出其中最大的一个数。

---

1，什么是算法？试从日常生活中找3个例子，描述它们的算法。

算法：简而言之就是求解问题的步骤，对特定问题求解步骤的一种描述。比如：菜谱，上面清楚的描述了每道美食需要什么食材，按照什么方式步骤进行烹饪，最后就可以得到香气喷喷的菜肴。

比如生活中的例子：

1.刷牙

• 取出牙膏和牙刷
• 挤牙膏
• 把牙膏抹在牙刷上
• 洗刷刷洗刷刷，哦啊，哦啊
• 漱口
• 放好牙刷

?2.从家到学校

• 出门右拐
• 步行5分钟到公交站
• 坐5站公交车
• 沿人行道步行100米后右转
• 到达学校门

3.找女朋友

• 苦心钻研编程
• 参加各种编程大赛成为大神
• 给心仪的女神讲编程题获取好感
• 用程序写浪漫的表白软件
• 女神同意，升级为女朋友

2，什么叫结构化的算法？为什么要提倡结构化的算法？

结构化算法：由一些顺序，选择，循环等基本结构按照顺序组成，在基本结构之间不存在向前或向后的跳转，流程的控制只存在于一个基本的范围之内。

非结构化算法，流程不受限制的随意跳来跳去，使流程图毫无规律。使人在阅读的时候难以理解算法的逻辑。难以阅读，也难以修改。从而使算法的可靠性和可维护性难以保证。

而结构化算法便于编写，可读性高，修改和维护起来简单，可以减少程序出错的机会，提高了程序的可靠性，保证了程序的质量，因此提倡结构化的算法。

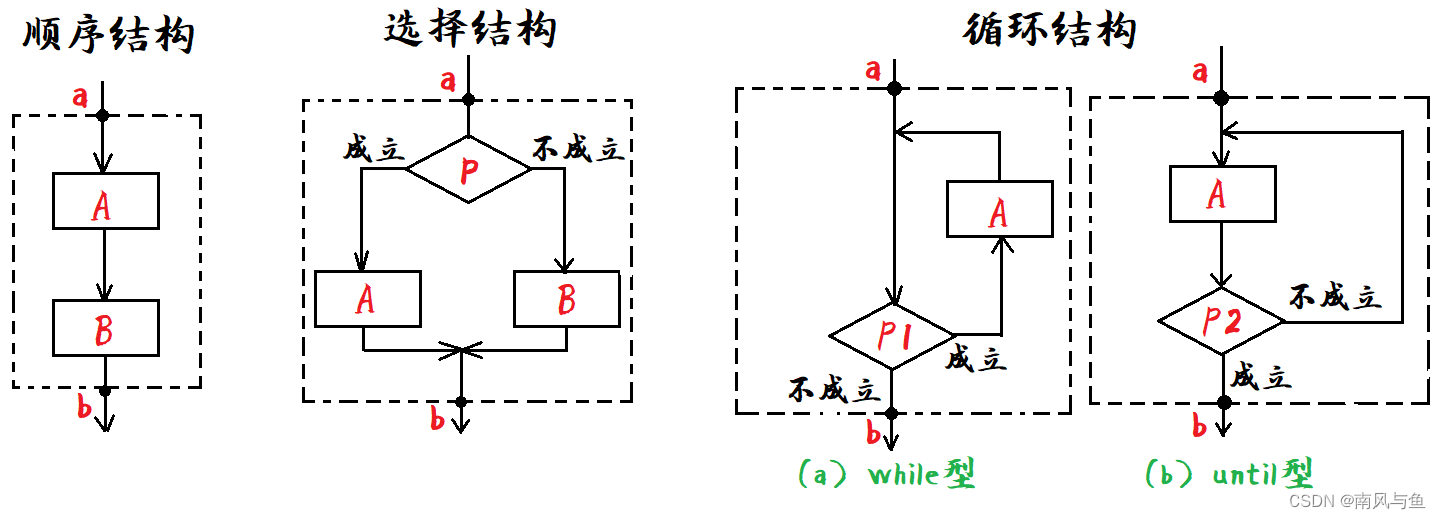
3，试述3种基本结构的特点，请另外设计两种基本结构（要符合基本结构的特点）。

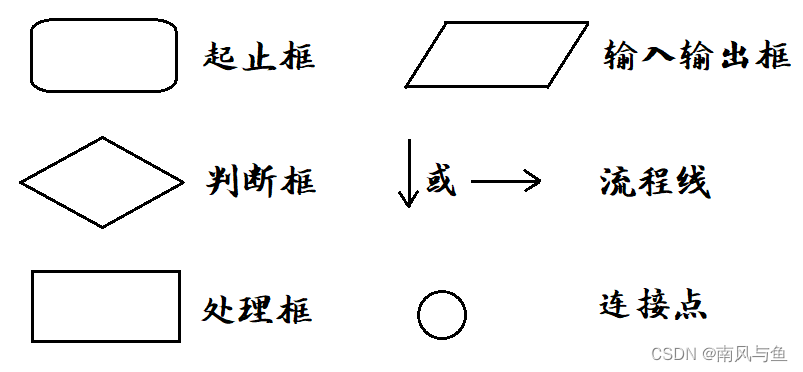
结构化程序设计方法主要由以下三种基本结构组成：

1.顺序结构：顺序结构是一种线性，有序的结构，它依次执行各语句模块。

比如：娶了媳妇之后，才能生娃。

2.选择结构：选择结构是根据条件成立与否选择程序执行的通路。

比如：如果天上掉馅饼，我就做你的女朋友，否则你找你的傻白甜，我找我的高富帅。

3.循环结构：循环结构是重复执行一个或几个模块，直到满足某一条件位置。

比如：你连续给我讲100天笑话我就答应做你女朋友。

网上一个循环的笑话：

总裁对秘书说：这几天我带你去北京走走，你准备下。

秘书打电话给老公：这几天我要和老总去北京开会，你自己照顾自己。

老公给情人打电话：我老婆这几天要去北京出差，我们也出来玩吧。

情人给辅导功课的小男孩打电话：这几天不用上课，我有事情。

小男孩给爷爷打电话：爷爷，这几天老师有事，不用上课，你陪我玩吧。

爷爷给秘书打电话：我这几天要陪孙子玩，不能去北京了。

秘书给老公打电话：这几天老总有急事，我们不去北京开会了。

老公给情人打电话：这几天不能出来玩，我老婆不去北京了。

情人给辅导功课的小男孩打电话：这几天继续正常上课。

小男孩给爷爷打电话：爷爷，这几天还是要上课，我不能陪你玩了。

爷爷给秘书打电话：这几天我还是带你去北京走走的，你准备下。

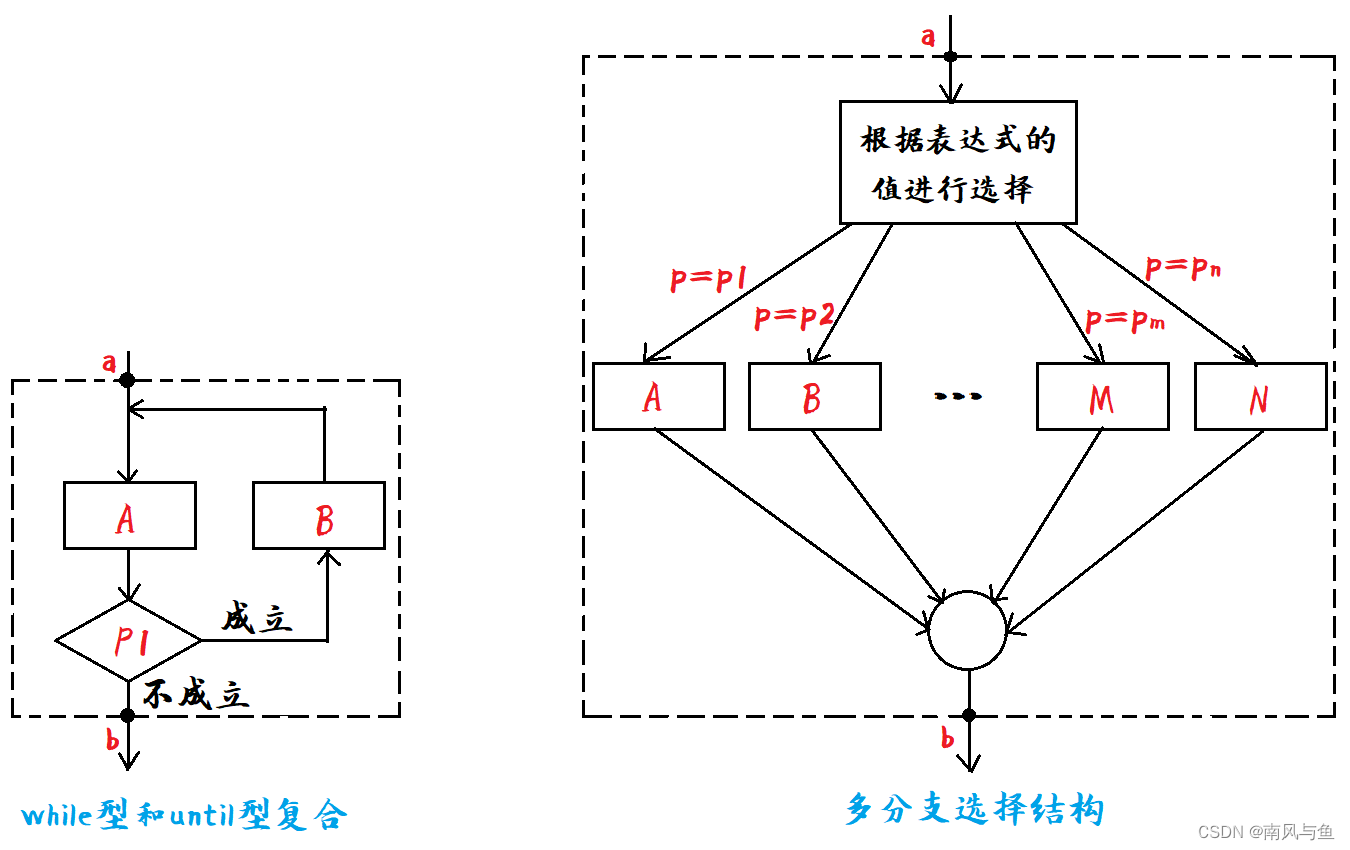
重新设计基本结构要满足以下几点：

1. 只有一个入口
2. 只有一个出口
3. 结构内的每一部分都有机会执行到
4. 结构内不存在死循环

因此给出以下结构：while型和until型循环复合结构以及多分支选择结构

4，用传统流程图表示求解以下问题的算法。

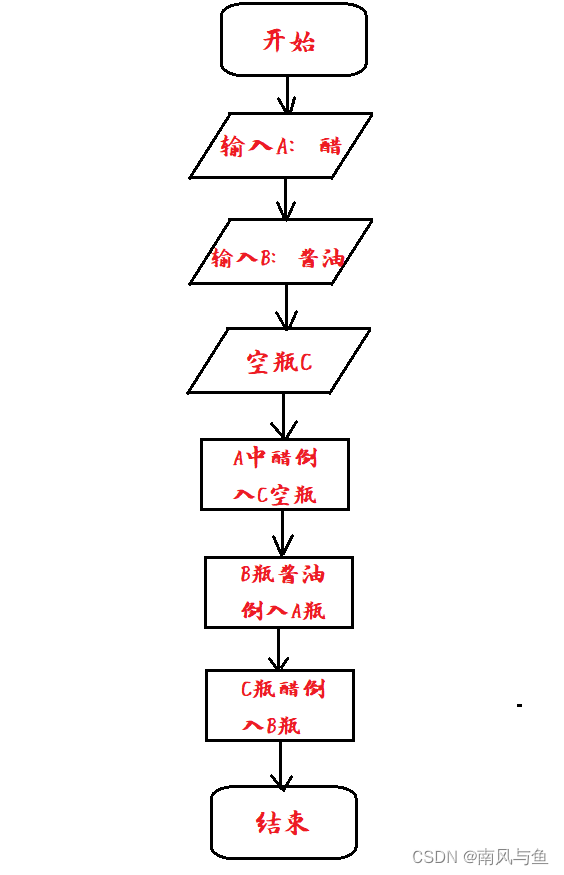
（1）有两个瓶子A和B，分别盛放醋和酱油，要求将它们互换。

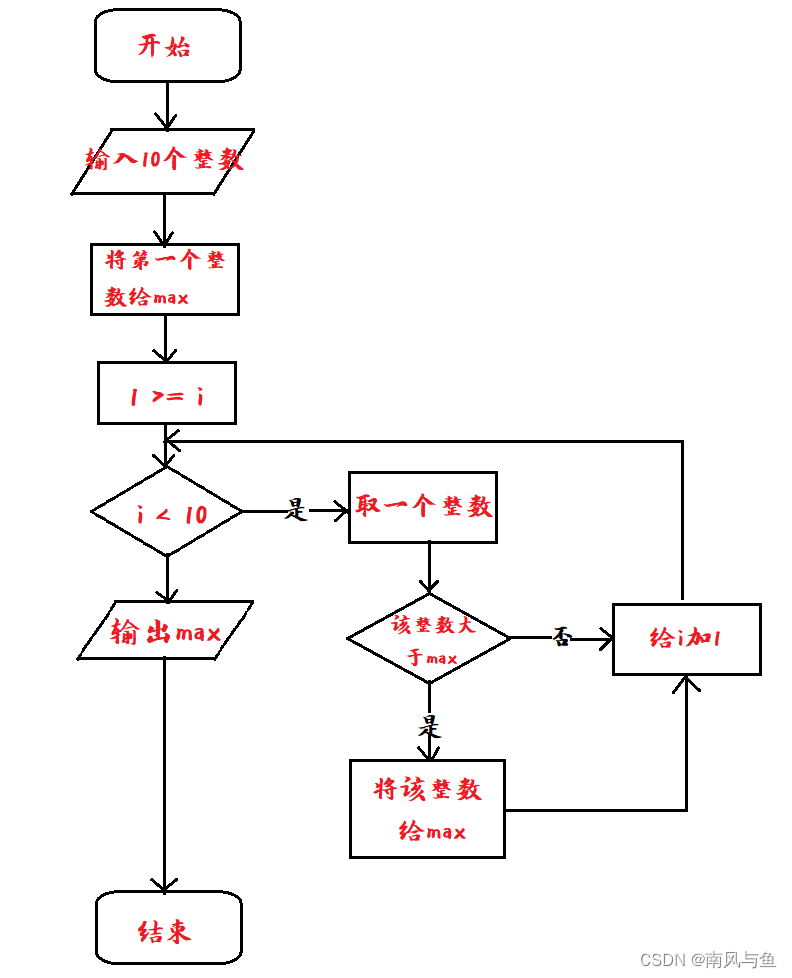
（2）依次将10个数输入，要求输出其中最大的数。

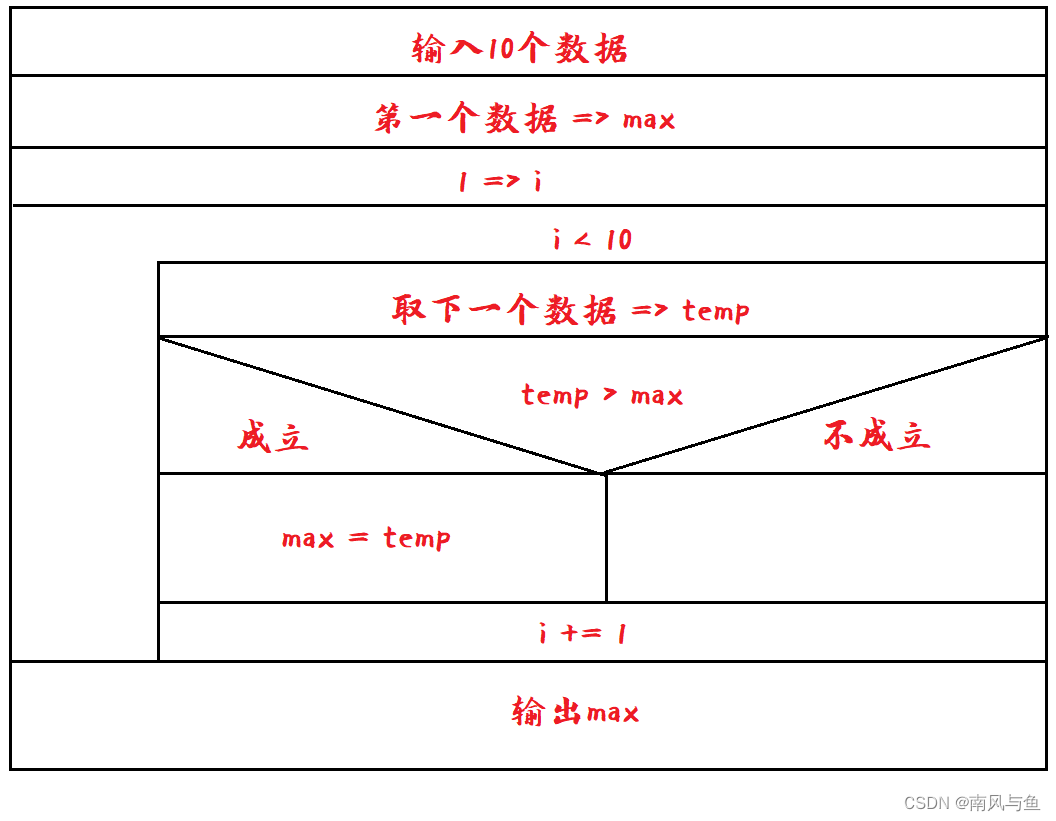
解析：先输入10个整数，将第一个整数给max，然后依次取剩余整数与max进行比较，如果某个整数大于max，将该整数交给max，直到所有剩余整数全部比较完，max中保存的即为最大整数，将max值输出。

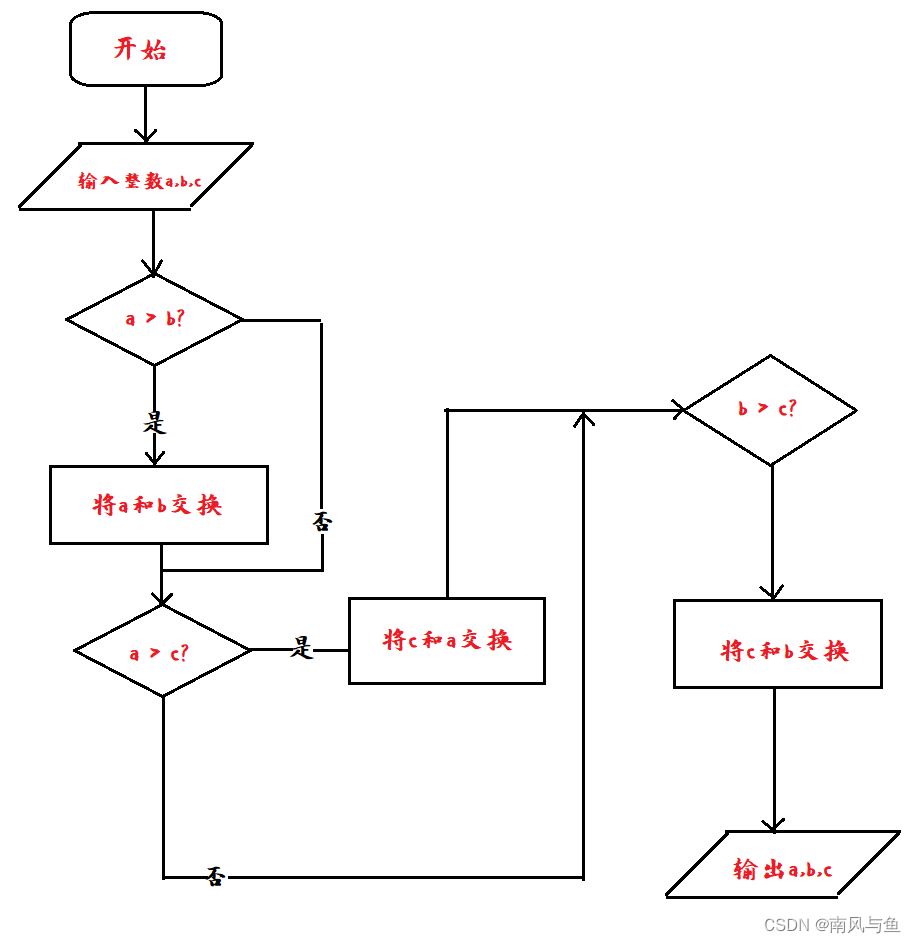
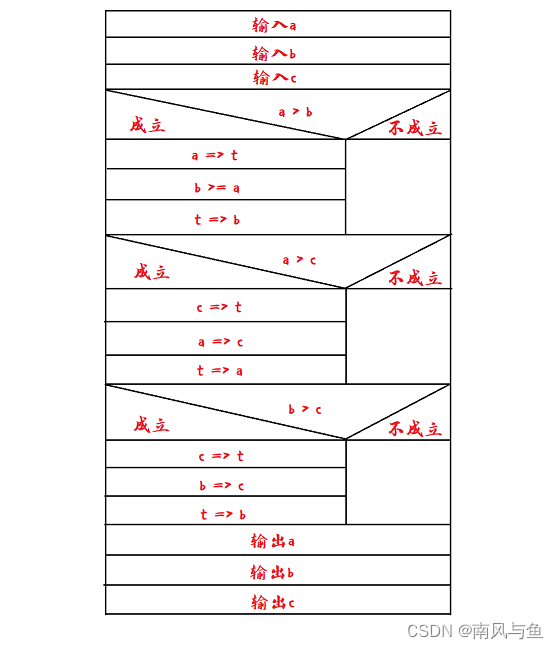
（3）有3个数a,b,c，要求按大小顺序把它们输出。

解析：

1. 先用a和b比较，如果a大于b，将a与b内容交换（a是a,b较小者），否则进行第二步
2. 用c和a比较，如果a大于c，将a和c交换（a是a和c中较小者，即a,b,c中最小），否则进行第四步
3. 用c和b比较，如果b大于c，将c和b交换（b是b,c中的小者，也是三者中次小者），否则进行第四步
4. 输出a,b,c，结束

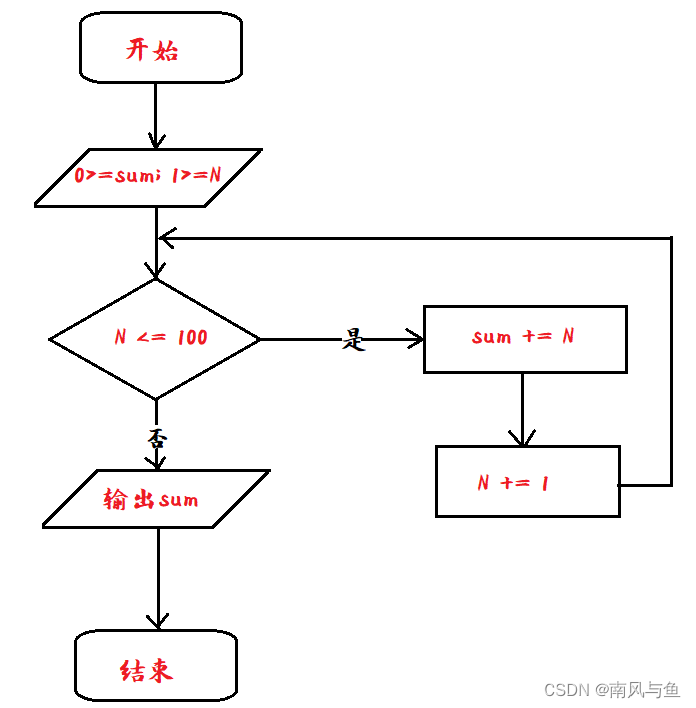
（4）求1+2+3+...+100。

解析：

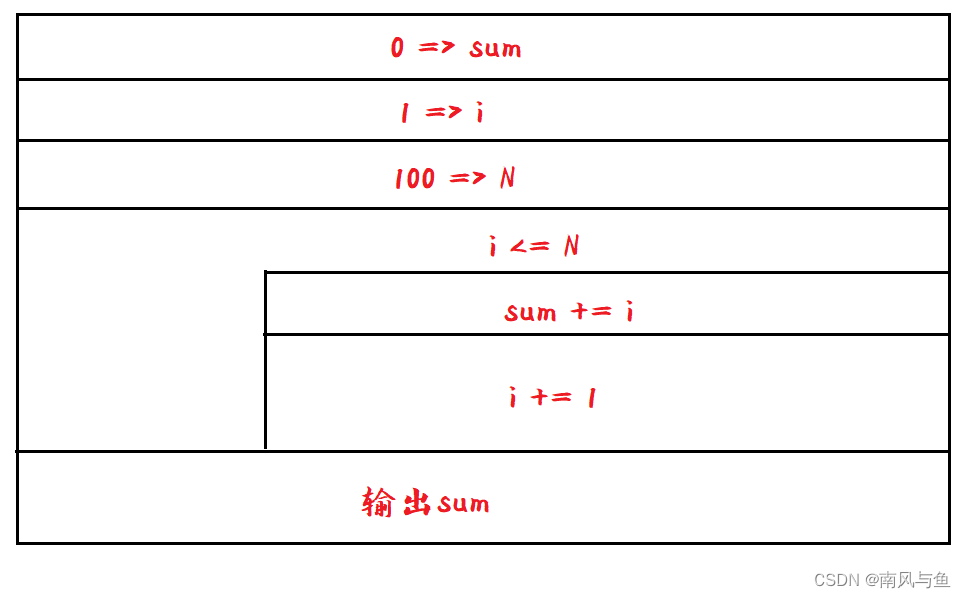
给定N为1，sum为0，如果N小于等于100时，进行sum += N，直到N超过100，循环操作完成后sum即为从1加到100的结果。

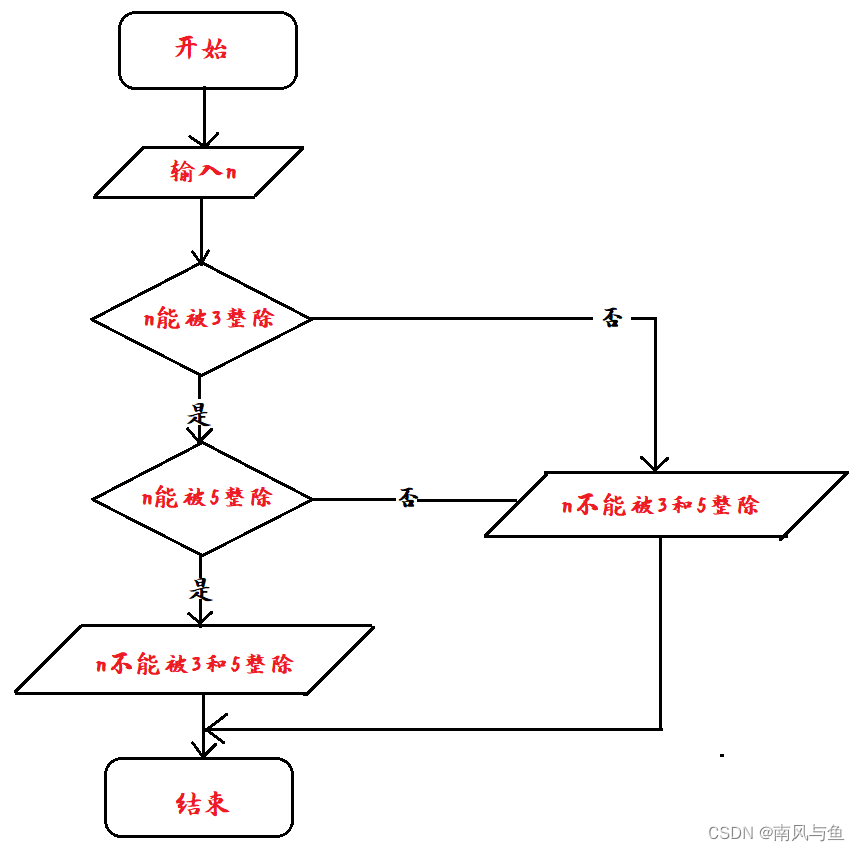
（5）判断一个数n能否同时被3和5整除。

解析：

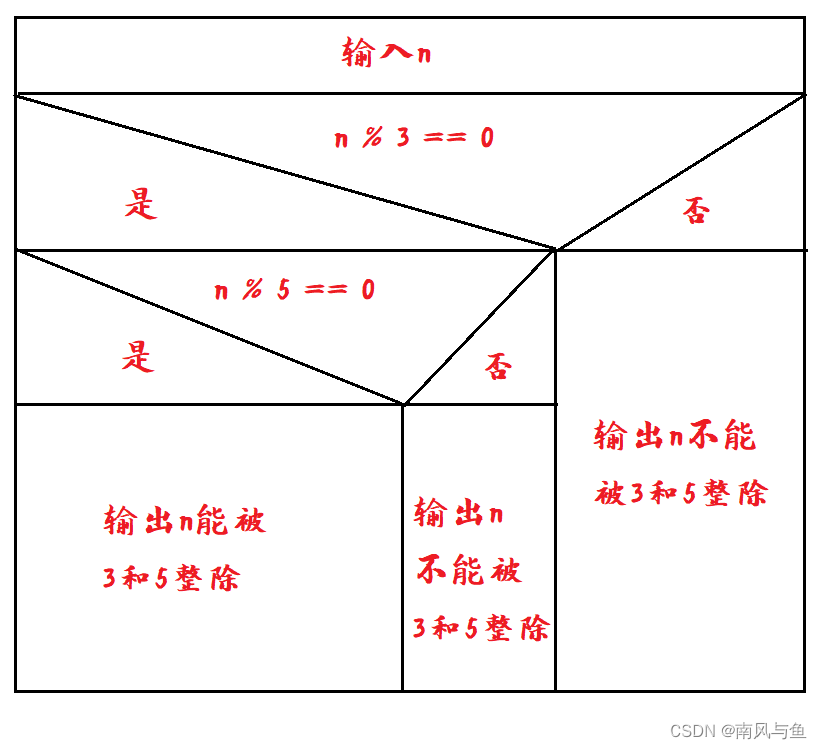
1. 输入数据n
2. 如果n能被3整除，进行第三步，否则输出n不能被3和5整除
3. 如果n能被5整除，输出n能被3和5整除，否则n不能被3和5整除

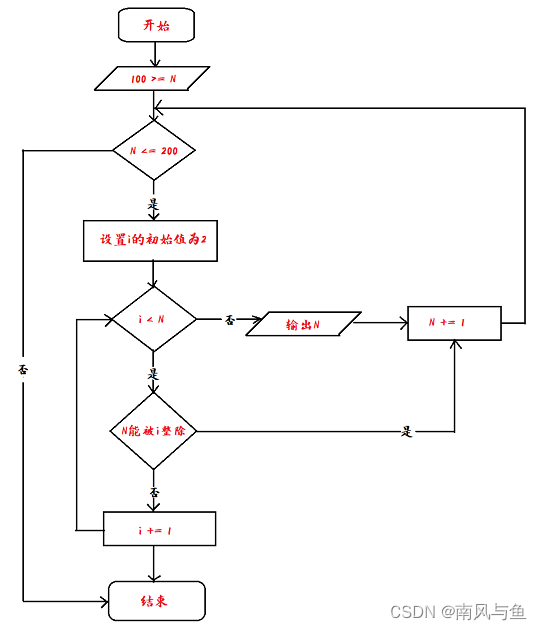
（6） 将100~200之间的素数输出

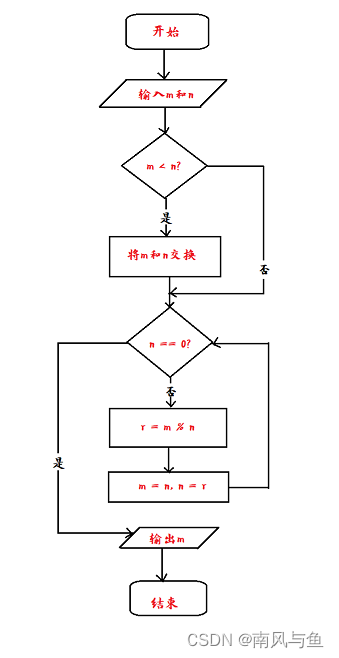
（7）求两个数m和n的最大公约数

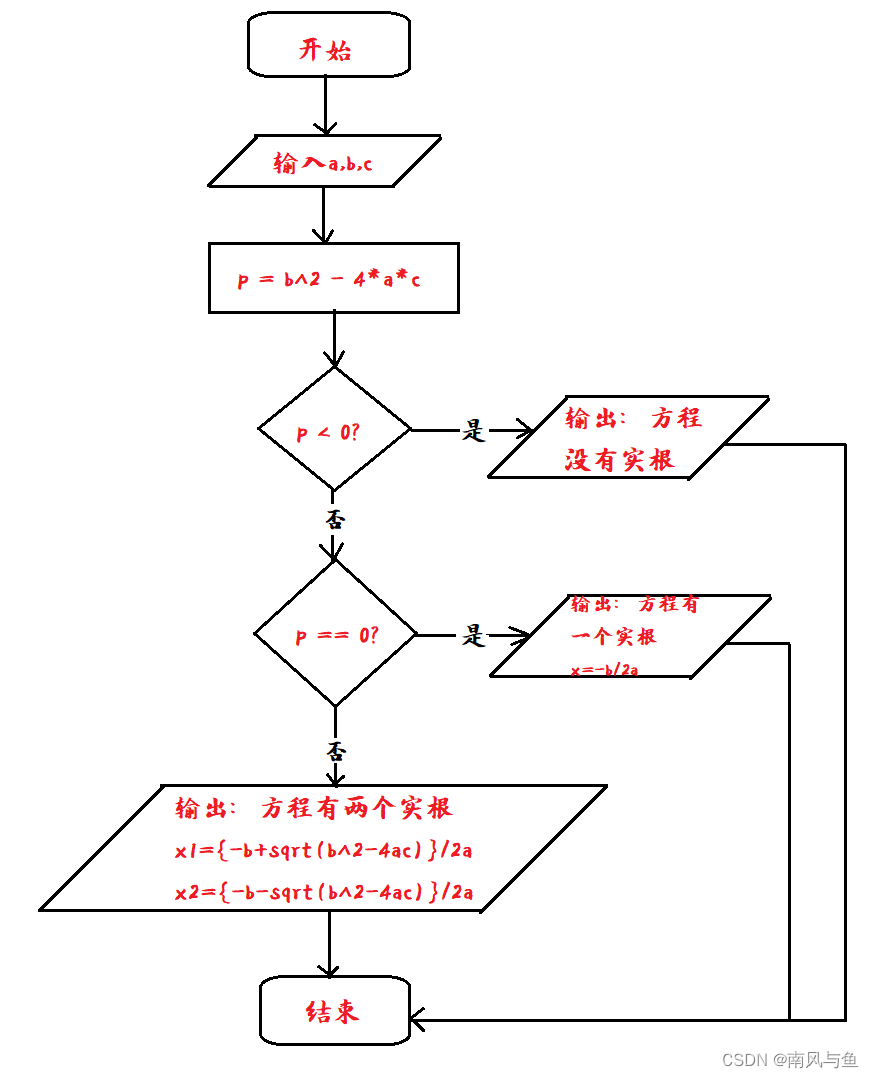
（8）求方程ax^2 + bx + c = 0的根。分别考虑：

a.有两个不相等的实根

b.有两个相等的实根?

5.用N-S图表示第4题中各题的算法。

（1）有两个瓶子A和B，分别盛放醋和酱油，要求将它们互换。

（2）依次将10个数输入，要求输出其中最大的数。

（3）有3个数a,b,c，要求按大小顺序把它们输出。

（4）求1+2+3+...+100。

（5）判断一个数n能否同时被3和5整除。

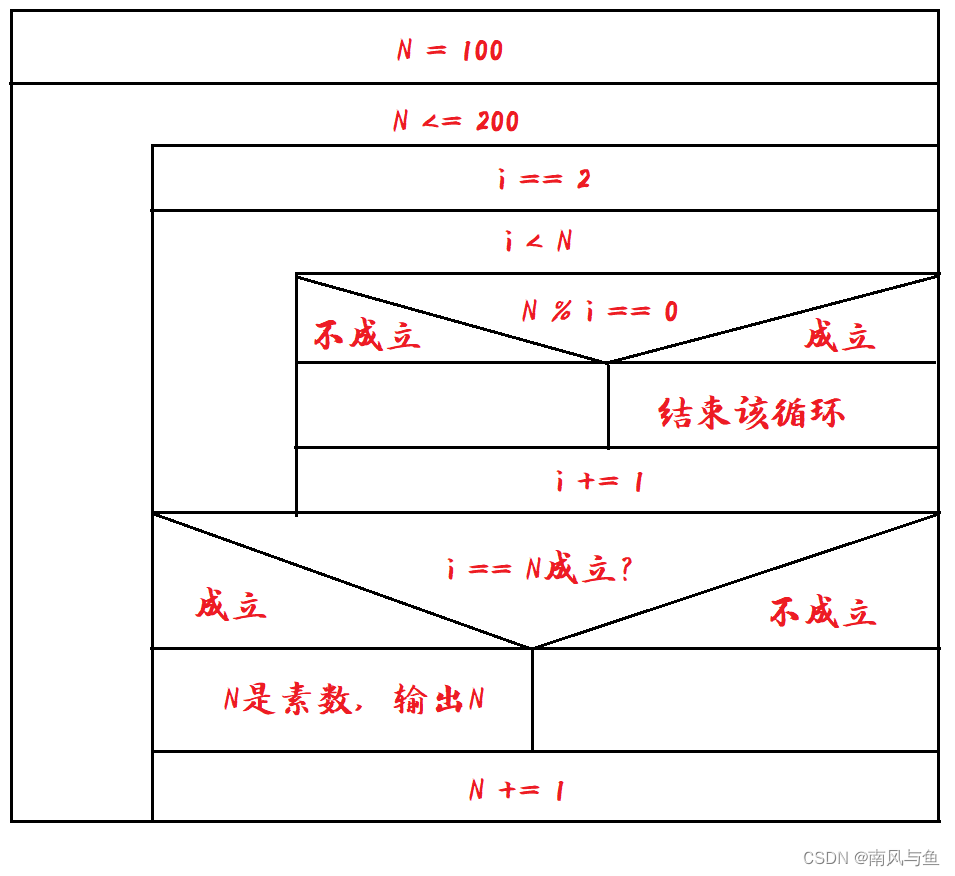
（6） 将100~200之间的素数输出。

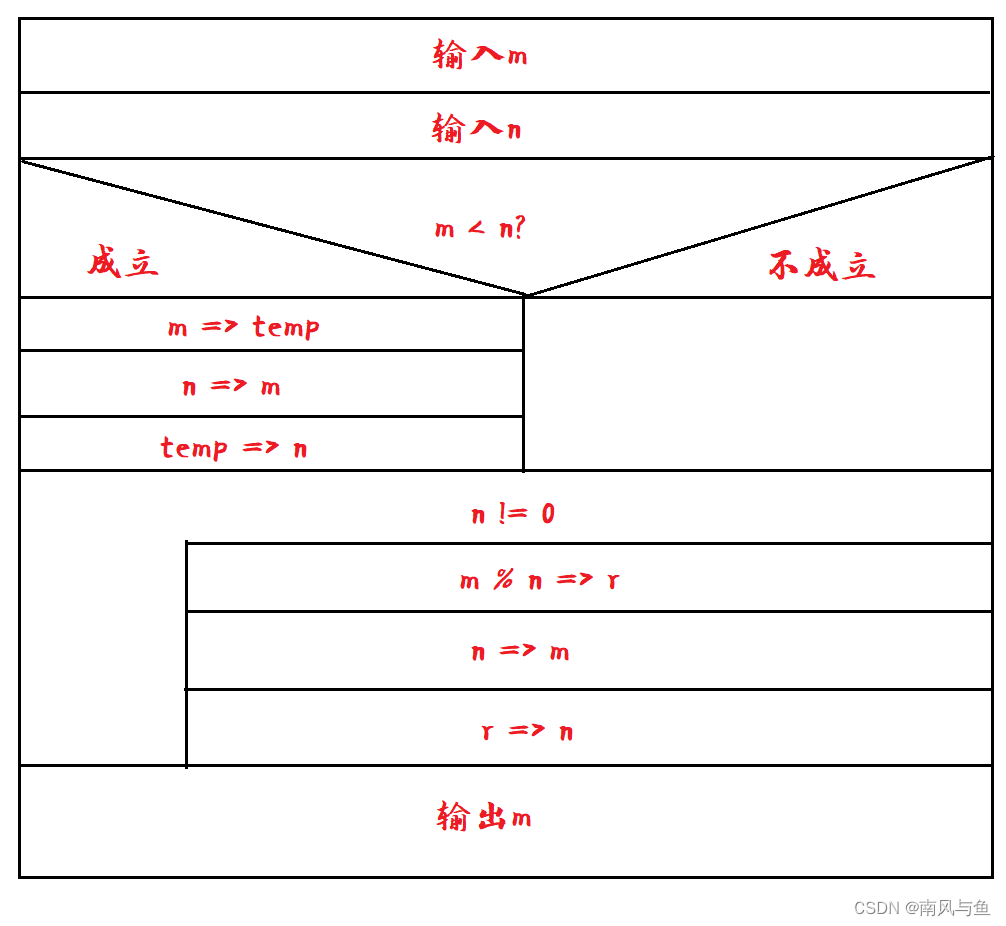
（7）求两个数m和n的最大公约数

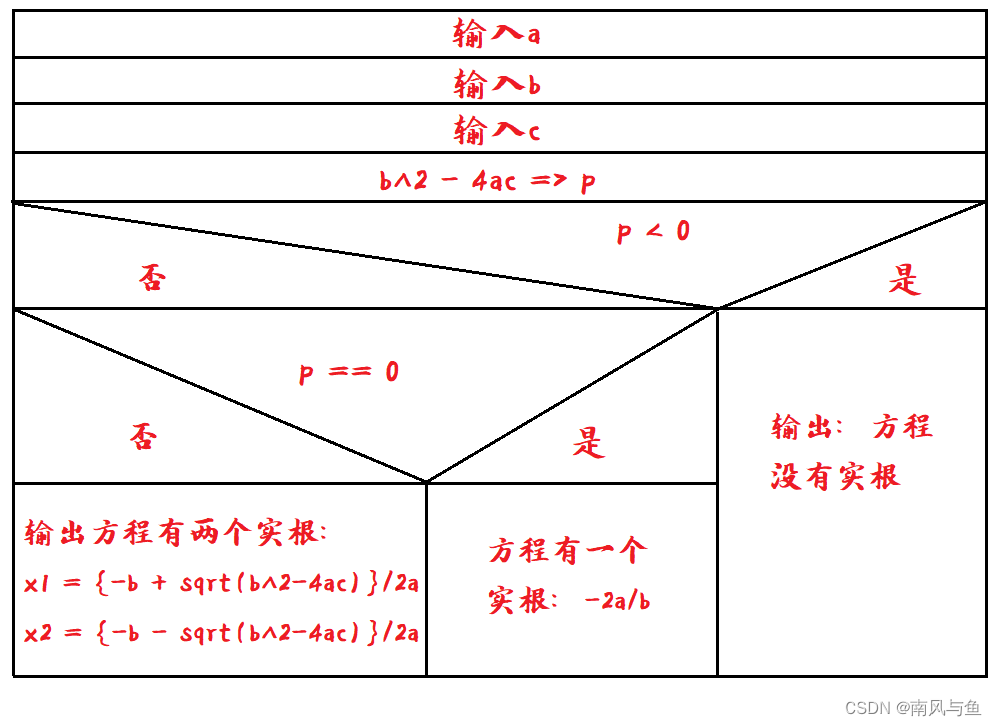
（8）求方程ax^2 + bx + c = 0的根。分别考虑：

a.有两个不相等的实根

b.有两个相等的实根?

6.用伪代码表示第4题中各题的算法。

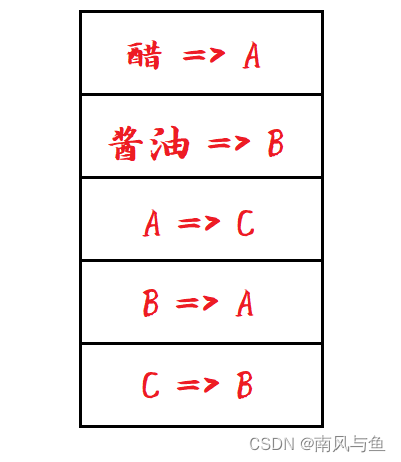
（1）有两个瓶子A和B，分别盛放醋和酱油，要求将它们互换。

begin
    醋 => A
    酱油 => B
    A => C
    B => A
    C => B
end

（2）依次将10个数输入，要求输出其中最大的数。

begin
    input 10个数据 => array
    array[0] => max

    //循环9次，依次取剩余的9个数据
    1 => i
    while i < 10
    {
        array[i] => temp
        if temp > max
        {
            temp => max
        }
        i + 1 => i
    }
    
    print max
end

（3）有3个数a,b,c，要求按大小顺序把它们输出。

begin
    input a
    input b
    input c

    if a > b
    {
        a => t
        b => a
        t => b
    }

    if a > c
    {
        c => t
        a => c
        t => a
    }
    
    if b > c
    {
        c => t
        b => c
        t => b
    }

    print a
    print b
    print c
end

（4）求1+2+3+...+100。

begin
    1 => i
    0 => sum
    while i <= 100
    {
        sum + i => sum
        i + 1 => i
    }

    print sum
end

（5）判断一个数n能否同时被3和5整除。

begin
    input n
    if n % 3 == 0
    {
        if n % 5 == 0
        {
            print n能被3和5整除
        }
        else
        {
            print n不能被3和5整除
        }
    }
    else
    {
        print n不能被3和5整除
    }
end

（6） 将100~200之间的素数输出。

begin
    100 => i
    200 => N
    while i <= N
    {
        2 => k
        while k < i
        {
            if i % k == 0
                break;
            
            k + 1 => k
        }
        if k == i
            print i
        i + 1 => i
    }
end

（7）求两个数m和n的最大公约数

begin
    input m
    input n

    if m < n
    {
        m => t
        n => m
        t => n
    }

    while n != 0
    {
        m % n => r
        m => n
        r => n
    }
    print m
end

（8）求方程ax^2 + bx + c = 0的根。分别考虑：

a.有两个不相等的实根

b.有两个相等的实根?

begin
    input a
    input b
    input c
    
    b*b - 4*a*c => p
    if p < 0
    {
        print 方程没有实根
    }
    
    if p == 0
    {
         print 方程有一个实根 -b/2a
    }
    
    if p > 0
    {
        print 方程有两个实根
        print x1 = {-b + sqrt(b^2 - 4ac)}/2a
        print x2 = {-b - sqrt(b^2 - 4ac)}/2a
    }
end

7.什么叫结构化程序设计？它的主要内容是什么？

当面临一个复杂的问题时，很难一下子写出一个层次分明、结构清晰、算法正确的程序。

结构化程序设计是进行以模块功能和处理过程设计为主的详细设计原则。它的主要观点是采用自顶向下、逐步求精的程序设计方法；即首先把一个复杂的大问题分解为若干个相对独立的小问题。然后，对每个小问题编写出一个功能上相对独立的程序块（模块）。最后将各程序块组装成一个完整的程序。

具体来说，采用以下方法得到结构化程序：

1.自顶向下

程序设计时，应先考虑总体，后考虑细节，不要一开始就过多追求众多的细节，先从最上层总目标开始设计，逐步使问题具体化。

2.逐步细化

对复杂问题，应设计一些子目标作为过渡，逐步细化。

3.模块化设计

一个复杂问题，肯定是由若干稍简单的问题构成。模块化是把程序要解决的总目标分解为子目标，再分解为具体的小目标，把每一个小目标称为一个模块。

4.结构化编码

编码实现

8.用自顶向下，逐步细化的方法进行以下算法的设计：

（1）输出1900 --- 2000年中是闰年的年份，符合下面两个条件之一的年份是闰年。

a、能被4整除但不能被100整除

b、能被100整除且能被400整除

算法大体流程：

1.循环取1900~2000中的每一个年份

2.对于每一个年份判断其是否是闰年

3.是闰年则输出

（2）求ax^2 + bx + c = 0的根。分别考虑d = b^2 - 4ac 大于0、等于0和小于0的情况。

1.获取a,b,c的值

2.计算b^2 - 4ac的结果并给p

3.如果p < 0，则方程没有实根

4.如果p == 0，则方程有一个实根 -b/2a

5.如果p > 0，则方程有两个实根 x1 = {-b + sqrt(b^2 - 4ac)}/2a? ?x2 = {-b - sqrt(b^2 - 4ac)}/2a

（3）输入10个数，输出其中最大的一个数。

1.给一个max保存最大值

2.分别输入10个数，并用每个数与max进行比较，如果该数大于max，则将该数给max

3.输出max