判定一个点是否在三角形内

介绍

最近在给我们足球项目加入足球减速区域，这里要求球场两侧是长方形但是球门两侧是需要使用三角形减速器（主要也是怕射门的时候球会进出减速），下面我会介绍几个检测的思想外加一个比较简单的检测方法。
其实方法很多面积检测法，边界检测法、重心检测法、射线检测等

方案一（面积检测）

这里我只提供一个思路，可以通过计算点与三角形的三个顶点构成的三个子三角形的面积之和与三角形本身的面积进行比较来判断点是否在三角形内。如果三个子三角形的面积之和等于三角形本身的面积，则点在三角形内；否则，点在三角形外。

如图所示（点在三角形外侧）：三角形ABC和检测点D

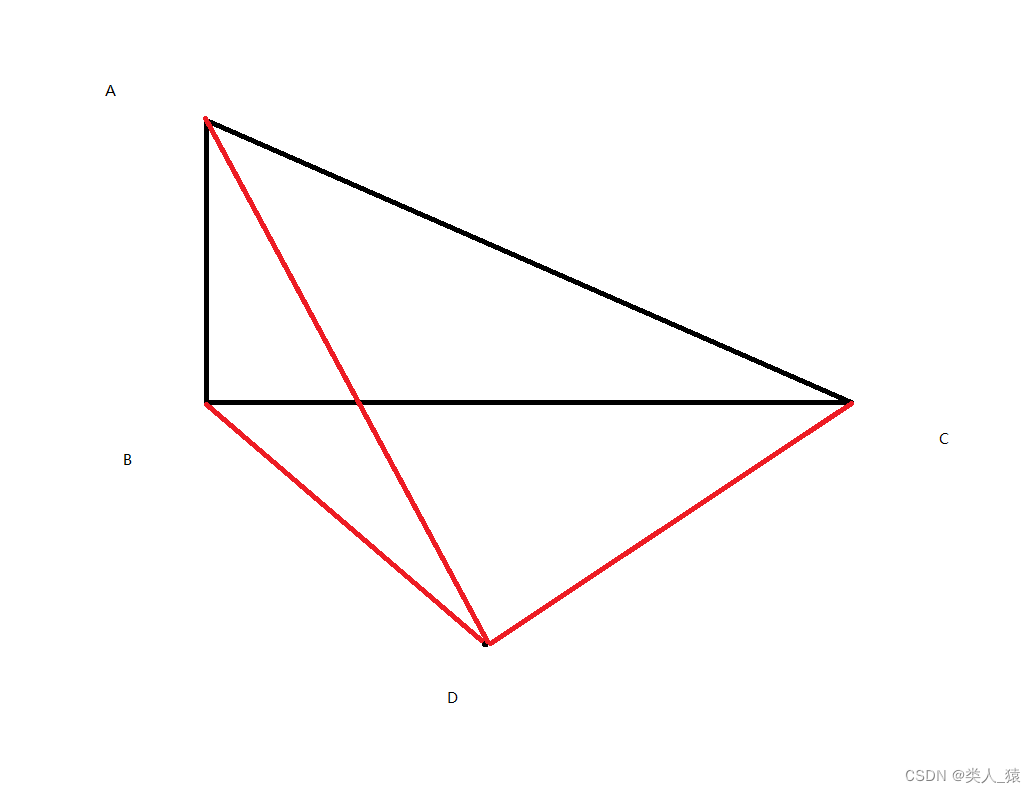
上述以检测点D为一端点分别连接A、B、C三个点构成三个三角形分贝为△ABD、△ACD、△BCD
很明显三个三角形的面积之和必然大于△ABC的面积，所以检测点D在△ABC的外侧

如图所示（点在三角形内侧）：三角形ABC和检测点D

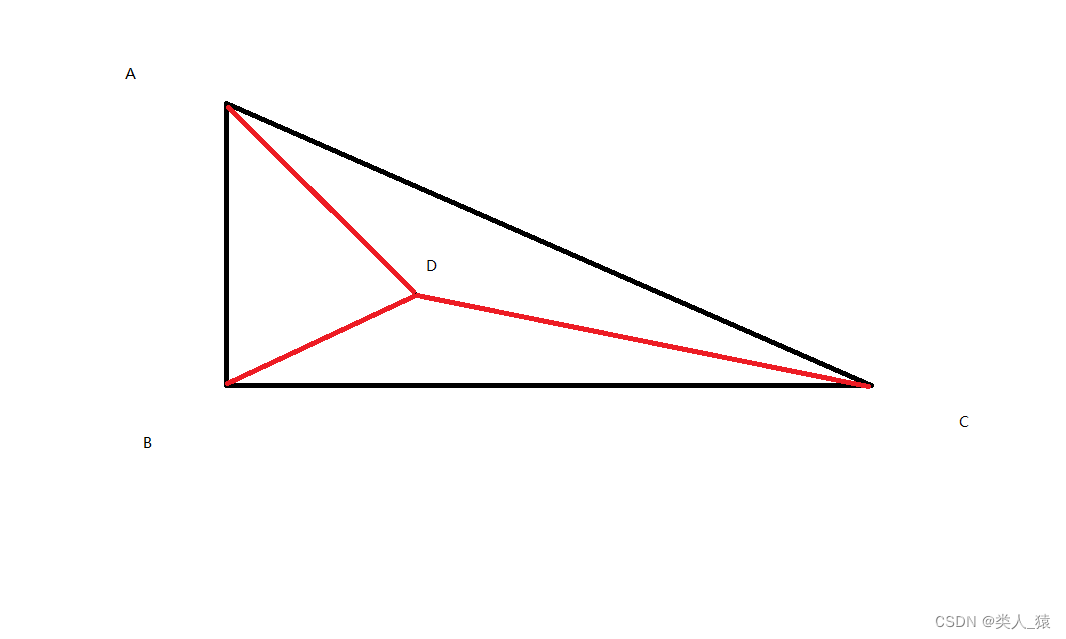
上述以检测点D为一端点分别连接A、B、C三个点构成三个三角形分贝为△ABD、△ACD、△BCD
明显三个三角形的面积之和等于△ABC的面积，所以检测点D在△ABC的内侧

方案二（边界检测）

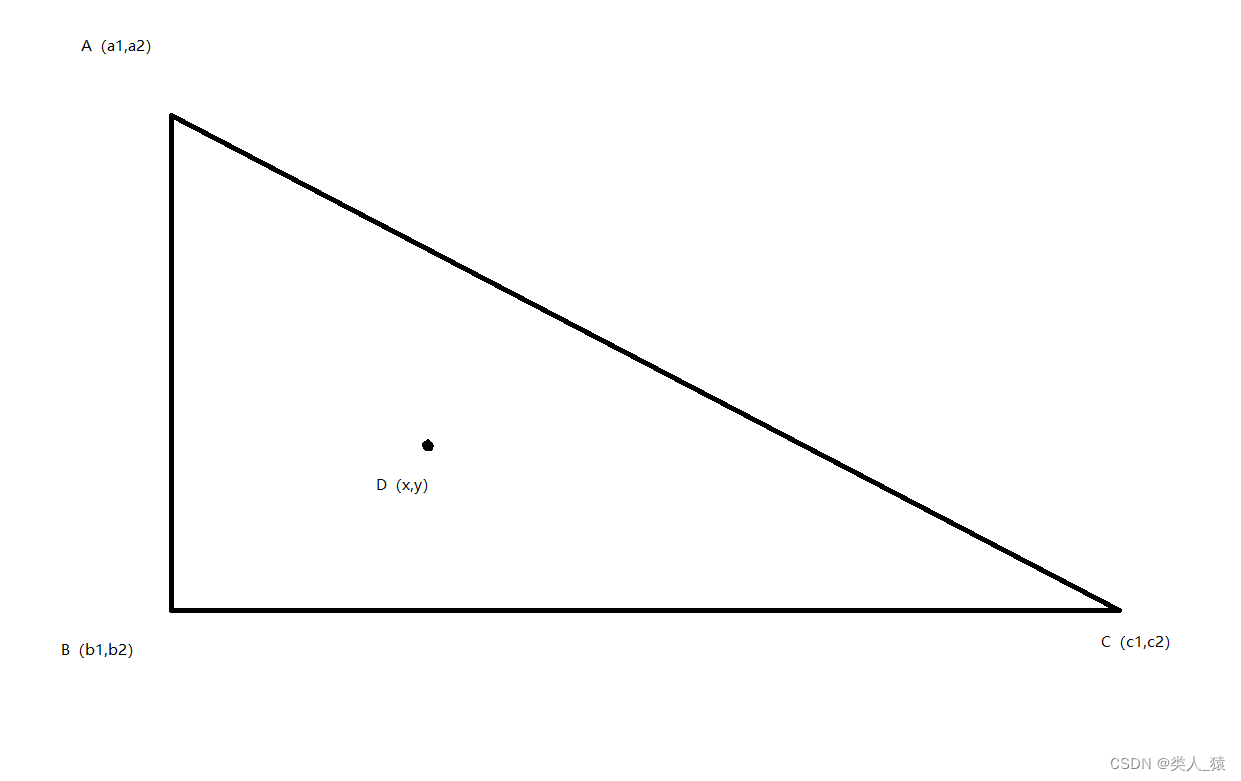
通过判断点与三角形的三条边的方程的正负性来判断点是否在三角形内如下

三角形三个顶点为A(a1,a2),B(b1,b2),C(c1,c2)和检测点D(x,y)。判断点D是否在三角形内，需满足下面两点：

1. fb(x,y) * fb(b1,b2) > 0
2. fc(x,y) * fc(c1,c2) > 0
   其中fa(x,y),fb(x,y),fc(x,y)分别为点D与三角形的三条边BC，AC，AB方程
   如果满足以上条件，则D在三角形内；否则，点在三角形外。

//这里我直接用Unity中的Transform来动态代替三角形，测试通过的代码如下可以进行检测

 bool PointInTriangle(Transform point, Transform pointA, Transform pointB, Transform pointC)
    {
        float x = point.position.x;
        float y = point.position.y;
        Vector3 A = pointA.position;
        Vector3 B = pointB.position;
        Vector3 C = pointC.position;

        float fa = IsInside(B.x, B.y, C.x, C.y, x, y);
        float fb = IsInside(C.x, C.y, A.x, A.y, x, y);
        float fc = IsInside(A.x, A.y, B.x, B.y, x, y);

        return fa * fb > 0 && fb * fc > 0 && fc * fa > 0;
    }
    float IsInside(float x1, float y1, float x2, float y2, float x, float y)
    {
        return (x - x1) * (y2 - y1) - (y - y1) * (x2 - x1);
    }

方案三（重心检测）

通过计算物体位置与三角形定点的关系，判定是否在三角形内。三角形内的点测试基于重心坐标，重心坐标就是一个点在三角形内的位置的一种方法，他使用三个系数（通常记为u、v、w）来表示点在三角形内的位置。

计算重心坐标：
计算测试点（testPoint）相对于三角形的三个顶点（p0、p1、p2）的重心坐标（u、v、w）。这可以通过以下公式计算

u = ((p1.y - p2.y) * (testPoint.x - p2.x) + (p2.x - p1.x) * (testPoint.y - p2.y)) /
    ((p1.y - p2.y) * (p0.x - p2.x) + (p2.x - p1.x) * (p0.y - p2.y));

v = ((p2.y - p0.y) * (testPoint.x - p2.x) + (p0.x - p2.x) * (testPoint.y - p2.y)) /
    ((p1.y - p2.y) * (p0.x - p2.x) + (p2.x - p1.x) * (p0.y - p2.y));

w = 1 - u - v;

检查点的位置：
如果重心坐标 u、v、w 都在 [0, 1] 的范围内，且它们的和等于 1，则表示测试点在三角形内。这是因为在标准的重心坐标系统中，u、v、w 的取值范围是 [0, 1]，它们的和等于 1

if (u >= 0f && v >= 0f && (u + v) <= 1f) {
    // 点在三角形内
    return true;
} else {
    // 点在三角形外
    return false;
}

完整检测代码如下：

bool IsObjectInsideTriangle(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 testPoint)
    {
        // Calculate barycentric coordinates
        float u = ((p1.y - p2.y)*(testPoint.x - p2.x) + (p2.x - p1.x)*(testPoint.y - p2.y)) /
                  ((p1.y - p2.y)*(p0.x - p2.x) + (p2.x - p1.x)*(p0.y - p2.y));

        float v = ((p2.y - p0.y)*(testPoint.x - p2.x) + (p0.x - p2.x)*(testPoint.y - p2.y)) /
                  ((p1.y - p2.y)*(p0.x - p2.x) + (p2.x - p1.x)*(p0.y - p2.y));

        // Check if the point is inside the triangle
        return (u >= 0f && v >= 0f && (u + v) <= 1f);
    }

总结

以上三种方法是我总结GPT和一些常规的方法，这是只是针对一个x，y轴（z轴默认相同，如果需要其他轴向可以自行进行修改）
希望能给大家提供帮助，感谢大家的支持。