注水算法—功率分配

发布时间：2024年01月06日

最近一直在学习一位学姐的知乎文章，文章链接放到下面了。

无线通信多用户MISO系统的发射功率最小化问题

这里面涉及到了注水算法，为了学习的更明白，写这篇博客方便以后能快速记起，如果内容有问题的地方，欢迎在评论区讨论。

注水（water filling）算法

注水（water filling）算法是一种功率分配算法，旨在为信道条件更好的用户分配更多的功率。

优化问题

一个基站对应多个用户

\mathop{\max}_{p} \sum_{k=1}^{K}{log_2(1+\frac{p_k}{\sigma^2}\left| h_k \right|^2)} (1) \\ s.t\;\;\sum_{k=1}^{K}{p_k} = P_{max} \\ p_k\geq 0, \forall k \in K \\

其中p_k表示第 k 个用户分配到的功率， |?_k|^2 表示第 k 个用户的信道增益。

并且所有用户的功率和不能 超过总的功率限制L({\bf{p}},\lambda) = \sum_{k=1}^{K}{log_2(1+\frac{p_k}{\sigma^2}\left| h_k \right|^2)} + \lambda(P_{max} - \sum_{k=1}^{K}{p_k}) (2) \\

\sum_{k=1}^{K}{p_k} = P_{max}( P_{max}为基站发射的总功率）

求解思路

该优化问题可以通过拉格朗日乘子法得到最优解

这里推荐两个讲的比较好的博客

优化-拉格朗日乘子法?

拉格朗日乘子法（Lagrange Multiplier Method）详解

原问题(1)，可以转换为：

L({\bf{p}},\lambda) = \sum_{k=1}^{K}{log_2(1+\frac{p_k}{\sigma^2}\left| h_k \right|^2)} + \lambda(P_{max} - \sum_{k=1}^{K}{p_k}) (2)

其中 \lambda∈R 是拉格朗日乘子。然后 L({\bf{p}},\lambda) 对 p_k的导函数为：

\frac{ \partial L({\bf{p}},\lambda) }{\partial p_k} = \frac{1}{ln2}\cdot\frac{\left| h_k \right|^2/ \sigma^2}{1 + p_k\left| h_k \right|^2/\sigma^2}- \lambda = 0 \\ p_k = \frac{1}{\lambda \cdot ln2} - \frac{\sigma^2}{\left| h_k \right|^2} \\

在这里为了表示方便，令\mu = \frac{1}{\lambda \cdot ln2}，因此

p_k = \mu- \frac{\sigma^2}{\left| h_k \right|^2} \\

由于 p_k≥0 这一约束条件的存在，于是有


p_k = max(\mu- \frac{\sigma^2}{\left| h_k \right|^2},0) \\
?

由于\sum_{k=1}^{K}{p_k} = P_{max}，则


\mu = \frac{P_{max} + \sum_{k=1}^{K}{\sigma^2/\left| h_k \right|^2}}{K}\\
?

\mu就是注水面。

结果


p_k = max(\mu- \frac{\sigma^2}{\left| h_k \right|^2},0) \\ \mu = \frac{P_{max} + \sum_{k=1}^{K}{\sigma^2/\left| h_k \right|^2}}{K}
?

用下图可以形象的表示注水算法

MATLAB代码实现

clc;
clear;

%% Simulation params
N               = 1;        % Number of transmit antennas
K               = 4;        % Number of users
P_max           = -10:5:30;  % maximum transmission power （dBm）
sigma_2         = 1;        % noise power
ch_realization  = 10;       % channel realizations

%% Generate Channles - Normalized Rayleigh fading channel
H = sqrt(1/2)*(randn(N,K,ch_realization)+1i*randn(N,K,ch_realization));

rate_water = zeros(ch_realization, length(P_max));

n = 1;
while (n < ch_realization + 1)
    n
    h = H(:,:,n);
    for j=1:length(P_max)
        p_max = db2pow(P_max(j));
        opt_p = zeros(K,1);
        sum1 = 0;
        for k=1:K
            sum1 = sum1 + sigma_2/(h(:,k)*h(:,k)');
        end
        mu = (p_max+sum1)/K;
        for k = 1:K
            opt_p(k) = max(mu - sigma_2/(h(:,k)*h(:,k)'),0);
        end
        rate_water(n,j) = rate(opt_p,h,sigma_2,K);
    end
    n = n+1;
end

plot(P_max,mean(rate_water,1),'or-','LineWidth',2)
hold on
grid on
xlabel('P_{max}(dBm)')
ylabel('Rate (bit/s/Hz)')
legend('waterFilling Method','Location','northwest')


function  r = rate(p,h,sigma_2,K)
    
sum = 0;
for k = 1:K
    sum = sum + log2(1+p(k)*(h(:,k)*h(:,k)')/sigma_2);
end
r = sum;
end

仿真结果

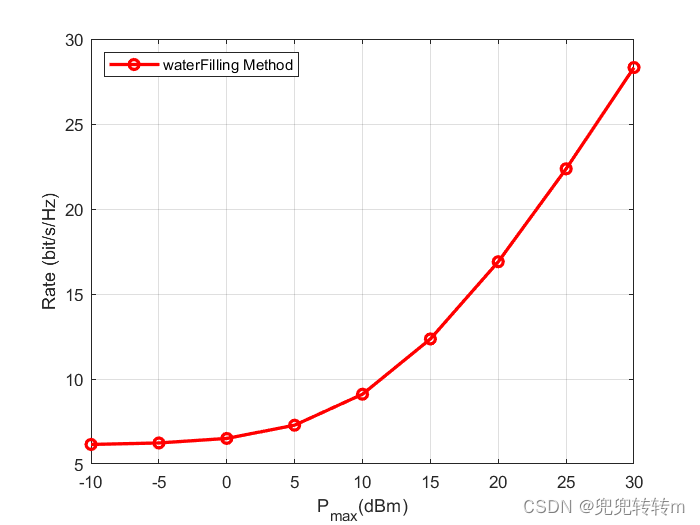
文章来源:https://blog.csdn.net/abc123mma/article/details/135423715
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章