2023年12月GESP认证C++等级考试（八级）真题试卷

发布时间：2023年12月20日

2023年12月GESP认证C++等级考试（八级）真题试卷

题目总数：27 ?? 总分数：100

选择题

第 1 题 ?? 单选题

小杨要从A城到B城，?想顺路游览?番。他有两个选项：1、坐?铁路到C城游览，再坐?铁或飞机到B城；?2、坐船到D城游览，再坐船、?铁或飞机到B城。请问?杨从A城到B城共有?种交通?案可以选择？（）。

第 2 题 ?? 单选题

以下哪个函数声明是符合语法的，且在调?时可以将?维数组的名字作为实际参数传递给形式参数a？（?）。

void?QuickSort(int?a[][10],?int?n);

void?QuickSort(int?a[5][],?int?m);

void?QuickSort(int?a[][],?int?n,?int?m);

void?QuickSort(int?**?a,?int?n,?int?m);

第 3 题 ?? 单选题

下?有关C++类和对象的说法，错误的是（）。

对象的?命周期开始时，会执?构造函数。

对象的?命周期结束时，会执?析构函数。

类的析构函数可以为虚函数。

类的构造函数可以为虚函数。

第 4 题 ?? 单选题

使?邻接矩阵表达n个顶点的有向图，则该矩阵的??为（）。

n*(n+1)

n*n

n*(n-1)

n*(n-1)/2

第 5 题 ?? 单选题

5位同学排队，其中?位同学不能排在第?，则共有多少种可能的排队?式？（）。

120

第 6 题 ?? 单选题

?个?向图包含n个顶点，则其最??成树包含多少条边？（）。

n-1

n+1

最小生成树可能不存在。

第 7 题 ?? 单选题

已知三个double类型的变量a、b和theta分别表??个三角形的两条边长及?者的夹角（弧度），则?下列哪个表达式可以计算这个三角形的?积？（）。

a?*?b?*?sin(theta)?/?2

(a?+?b)?*?sin(theta)?/?2

a?*?b?*?cos(theta)?/?2

sqrt(a?*?a?+?b?*?b?-?2?*?a?*?b?*?cos(theta))

第 8 题 ?? 单选题

对有n个元素的?叉排序树进?中序遍历，其时间复杂度是（）。

O(1)

O(log(n))

O(n)

O(n2)

第 9 题 ?? 单选题

假设输?参数m和n满?m=<n??，则下?程序的最差情况的时间复杂度为（）。

O(log(n))

O(n)

O(n*m)

O(m*log(n))

第 10 题 ?? 单选题

下?程序的时间复杂度为（）。

O(n)

O(an)

O(log(n))

O(log(n)*a)

第 11 题 ?? 单选题

下?程序的时间复杂度为（）。

O(2n)

O(2m?*(n-m))

O(C(n,m))

O(m*(n-m))

第 12 题 ?? 单选题

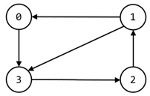
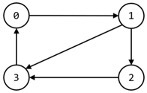
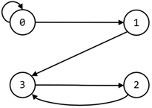
下?的程序使?出边的邻接表表达有向图，则下列选项中哪个是它表达的图？（）

第 13 题 ?? 单选题

下?程序的输出为（）。

第 14 题 ?? 单选题

下?程序的输出为（）。

第 15 题 ?? 单选题

下?的程序中，?维数组h和v分别代表如下图所?的?格中的?平边的时间消耗和垂直边的时间消耗。?程序使?动态规划计算从左下角到右上角的最?时间消耗，则横线处应该填写下列哪个选项的代码？（）。

dis[i][j]?=?min(dis[i?-?1][j]?+?v[i?-?1][j],?dis[i][j?-?1]?+?h[i][j?-?1]);

dis[i][j]?=?min(dis[i?-?1][j]?+?h[i?-?1][j],?dis[i][j?-?1]?+?v[i][j?-?1]);

dis[i?+?1][j?+?1]?=?min(dis[i][j?+?1]?+?v[i][j?+?1],?dis[i?+?1][j]?+?h[i?+?1][j]);

dis[i?+?1][j?+?1]?=?min(dis[i][j?+?1]?+?h[i][j?+?1],?dis[i?+?1][j]?+?v[i?+?1][j]);

判断题

第 16 题 ?? 判断题

C++语??常强?，可以?来求解?程的解。例如，如果变量x为double类型的变量，则执?语句x?*?2?-?4?=?0;后，变量x的值会变为2.0。

正确

错误

第 17 题 ?? 判断题

?个袋?中有3个完全相同的红??球、2个完全相同的蓝??球。每次从中取出1个，且不放回袋?，这样?进?3次后，将取出的?球依次排列，则可能的颜?顺序有7种。

正确

错误

第 18 题 ?? 判断题

杨辉三角，是?项式系数的?种三角形排列，在中国南宋数学家杨辉1261年所著的《详解九章算法》?书中?出现，是中国数学史上的?项伟?成就。

正确

错误

第 19 题 ?? 判断题

N个顶点的有向完全图（不带?环）有? N*(N-1)/2?条边。

正确

错误

第 20 题 ?? 判断题

如果待查找的元素确定，只要哈希表的??不?于查找元素的个数，就?定存在不会产?冲突的哈希函数。

正确

错误

第 21 题 ?? 判断题

动态规划算法的时间复杂度?般为：必要状态的数量，乘以计算?次状态转移?程的时间复杂度。

正确

错误

第 22 题 ?? 判断题

已知int类型的变量a、b和h中分别存储着?个梯形的顶边长、底边长和?，则这个梯形的?积可以通?过表达式(a?+?b)?*?h?/2求得。

正确

错误

第 23 题 ?? 判断题

判断图是否连通只能??度优先搜索算法实现。

正确

错误

第 24 题 ?? 判断题

在?N个元素的?叉排序树中查找?个元素，最好情况的时间复杂度是???O(log N) ???。

正确

错误

第 25 题 ?? 判断题

给定double类型的变量x，且其值?于等于0，我们可以通过?分法求出???

????的近似值。

正确

错误

编程题

第 26 题 ?? 问答题

试题名称:奖品分配

班上有 N ?名同学，学号从 0 ? 到????N-1 ?。有??M?种奖品要分给这些同学，其中，第 i 种奖品总共有?ai??个（i=0,1,.....M-1 ）。巧合的是，奖品的数量不多不少，每位同学都可以恰好分到?个奖品，且最后剩余的奖品不超过1 ?个（即：

???）。

现在，请你求出每个班级礼物分配的?案数，所谓?案，指的是为每位同学都分配?个种类的奖品。只要有?位同?学获得了不同种类的奖品，即视为不同的?案。?便起见，你只需要输出?案数对??109+7 ?取模后的结果即可。

共有 ?T ? ?个班级都?临着奖品分配的问题，你需要依次为他们解答。

输入描述

第一行一个整数 T，表示班级数量。

接下来 T 行，每行若干用单个空格隔开的正整数。首先是两个正整数 N,M ，接着是 M个正整数

?。保证。

输出描述

输出 T 行，每行一个整数，表示该班级分配奖品的方案数对 109+7 取模的结果。

样例输入?1

<span style="color:#34495e"><span style="background-color:#ffffff">1??????3
2??????3?2?1?2?
3??????3?2?1?3?
4??????5?3?3?1</span></span>

样例输出?1

<span style="color:#34495e"><span style="background-color:#ffffff">1??????3?
2??????4?
3??????20</span></span>

样例解释1

对于第1?个班级，学号为?0,1,2 ?的同学可以依次分别获得奖品??0,1,1 ? ，也可以依次分别获得奖品????1,0,1 ? ?，也可以依次?分别获得奖品 ?1,1,0 ? ? ? ? ?，因此共有 ?3 ? 种?案。

对于第2?个班级，学号为???0,1,2 ? ? 的同学可以依次分别获得奖品???0,1,1???，也可以依次分别获得奖品 ???1,0,1? ? ，也可以依次?分别获得奖品??????1,1,1? ，也可以依次分别获得奖品?????1,1,1 ? ? ，因此共有 ?4 ? 种?案。

对于第3?个班级，可以把编号为 ?1 ? 的奖品分配给 ?5 ? 名同学中的任意?名，共有 ?5 ? 种?案；再把编号为 ?2 ? 的奖品分配?给剩余 ? 4 ?名同学中的任意?名，共有 4 ? ?种?案；最后给剩余 ? 3 ?名同学?然获得 ?0 ? 号奖品。因此，?案数为5*4=20。

样例输入?2

样例输出?2

数据规模

第 27 题 ?? 问答题

试题名称：?量的?作沟通

问题描述

某公司有 ? ?N ? 名员?，编号从 ?0 ? ????N-1 。其中，除了 ?0 ? 号员?是?板，其余每名员?都有?个直接领导。我们假设?编号为 i 的员?的直接领导是 ?fi?? 。?

该公司有严格的管理制度，每位员?只能受到本?或直接领导或间接领导的管理。具体来说，规定员? ?x ? 可以管理?员? y，当且仅当 ?x=y ? ? ? ? ?，或 ? x=fy? ? ，或 x ? ?可以管理 fy?? ? 。特别地，0号员??板只能?我管理，?法由其他任何员??管理。

现在，有?些同事要开展合作，他们希望找到?位同事来主持这场合作，这位同事必须能够管理参与合作的所有同?事。如果有多名满?这?条件的员?，他们希望找到编号最?的员?。你能帮帮他们吗？

输入描述

第???个整数 ?N ? ?，表?员?的数量。

第?????N-1 个?空格隔开的正整数，依次为 ?f1,f2,...fN-1?。?

第三??个整数 ?Q ? ，表?共有 ?Q ?场合作需要安排。

接下来??Q ??，每?描述?场合作：开头是?个整数?m（?

??），表?参与本次合作的员?数量；接着是 m个整数，依次表?参与本次合作的员?编号（保证编号合法且不重复）。

保证公司结构合法，即不存在任意?名员?，其本?是??的直接或间接领导。

输出描述

输出m 行，每行一个整数，依次为每场合作的主持人选。

样例输入1

<span style="color:#34495e"><span style="background-color:#ffffff">1??????5
2??????0?0?2?2?
3??????3
4??????2?3?4?
5??????3?2?3?4?
6??????2?14</span></span>

样例输出?1

<span style="color:#34495e"><span style="background-color:#ffffff">1??????2
2??????2?
3??????0</span></span>

样例解释1

对于第?场合作，员??3,4 有共同领导2，可以主持合作。?

对于第二场合作，员工2 本人即可以管理所有参与者。?

对于第三场合作，只有0老板才能管理所有参与者。

参考答案：2023年12月GESP认证C++等级考试（八级）真题试卷 | 6547网

文章来源:https://blog.csdn.net/m0_67260462/article/details/135112114
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！