投资的收益与风险问题2024.1.15
目录
问题:
给定种资产,每种资产有
的收益率和
的风险损失率(重点在风险而不是损失)。
假设每种购买,总投资为
。
每种资产在交易时还要缴费?
最终风险评定以为值
此外,还有银行,无风险无缴费?,收益为
。所以总投资选择为
,即
总净收益为收益减缴费
求同时
建立模型:
由于,所以
可以简化为
所以得出以下多目标规划模型:
目标函数为:
??????????? ??
约束为:
????????
模型转化:
对于本文题,求解多目标规划模型,采用约束法和线性加权法。
A:
?????????
约束法,即选择一个主要目标,而将其他目标放入约束条件中
????????????????例:
????????????????????????
????????????????????????
? ? ? ? ?????????对于取??则用?
?约束,对于取?
?则用?
?约束
????????则以下两种转化:
?????????选择
为主要目标,对风险进行固定约束
????????????????????????
????????????????????????
?????????选择
为主要目标,对净收益进行约束
????????????????????????
????????????????????????
?B:
?????????线性加权法,即将所有目标按照重要程度,分权整合为一个目标函数,求解新目标函数的最优(先化成同样类型,即同取
或同取
,再整合)
? ? ? ? ????????例:
????????????????????????
?????????????????????????
? ? ? ? ?则原模型转化为:
????????????????????????
????????????????????????
模型求解与分析
原题数据如下:
| 1 | 0.05 | 0 | 0 | 0 |
|---|---|---|---|---|
| 2 | 0.28 | 0.025 | 0.01 | 103 |
| 3 | 0.21 | 0.015 | 0.02 | 198 |
| 4 | 0.23 | 0.055 | 0.045 | 52 |
| 5 | 0.25 | 0.026 | 0.065 | 40 |
A.One:
对于的选取,由于要最小化风险,所以
的取值要较小,但不知道多小合适。
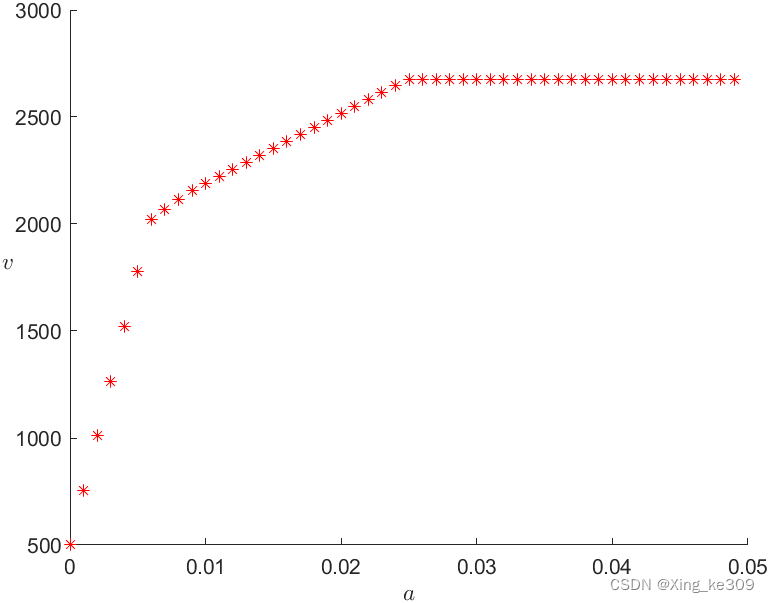
所以让从0开始,按步长为0.001增长,增到0.05(
已经很大了),进行绘图分析。
???????????????????????
????????????????????????
clc,clear,close all
c=[0.05,0.27,0.19,0.185,0.185];%ri-pi
prob=optimproblem("ObjectiveSense","max");
x=optimvar("x",5,1,"LowerBound",0);
prob.Objective=c*x;
b=[1,1.01,1.02,1.045,1.065];
M=10000;
prob.Constraints.con1=b*x==M;
a=0;aa=[];vv=[];xx=[];
%aa记录每次a的值,vv记录每次的结果,xx记录每次对应取值
q=[0.025,0.015,0.055,0.026]';
hold on
while a<0.05
prob.Constraints.con2=q.*x(2:end)<=a*M;
%matlab矩阵点乘,对应位置相乘但最终不会相加变为标量
%相加小于等于不代表分别小于等于,所以不能整合
[s,v]=solve(prob);
aa=[aa;a];
vv=[vv;v];
xx=[xx;s.x'];
a=a+0.001;
end
plot(aa,vv,"*r");
xlabel("$a$","Interpreter","latex");
ylabel("$v$","Interpreter","latex","Rotation",0);
disp(aa);
disp(vv);
disp(xx);
图像如下
?
1.0e+04 *
1.0000 0 0 0 0
0.8316 0.0400 0.0667 0.0182 0.0385
0.6633 0.0800 0.1333 0.0364 0.0769
0.4949 0.1200 0.2000 0.0545 0.1154
0.3266 0.1600 0.2667 0.0727 0.1538
0.1582 0.2000 0.3333 0.0909 0.1923
0 0.2400 0.4000 0.1091 0.2212
0 0.2800 0.4667 0.1273 0.1016
0 0.3200 0.5333 0.1271 0
0 0.3600 0.6000 0.0233 0
0 0.4000 0.5843 0 0
0 0.4400 0.5447 0 0
0 0.4800 0.5051 0 0
0 0.5200 0.4655 0 0
0 0.5600 0.4259 0 0
0 0.6000 0.3863 0 0
0 0.6400 0.3467 0 0
0 0.6800 0.3071 0 0
0 0.7200 0.2675 0 0
0 0.7600 0.2278 0 0
0 0.8000 0.1882 0 0
0 0.8400 0.1486 0 0
0 0.8800 0.1090 0 0
0 0.9200 0.0694 0 0
0 0.9600 0.0298 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
0 0.9901 0 0 0
由图和可以得出:
- 风险越大,收益越大
- 投资越分散,风险越小
- 在
之前存在拐点
,在
之前风险增长较慢而净收益增涨较快,之后则相反。所以
即为合适的取值。
缩小范围,进一步求。令阈值为0.01
图像如下
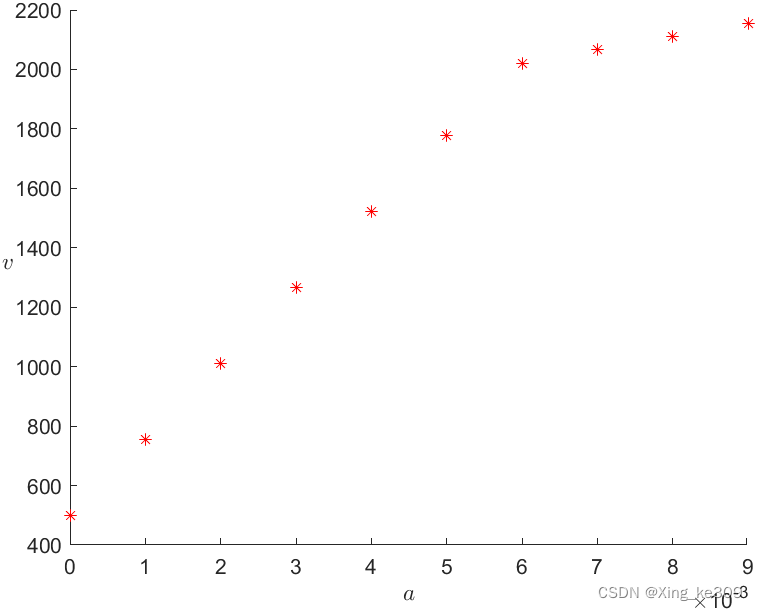
可以看出即为拐点,利用
找到对应数据。
即当时,此时净收益较大,且风险较小,最为合适。净收益为
,
取值为
A.Two:
目标函数为最大值最小化,则可以将最大值转换为约束条件
????????????????????????
????????????????????????
clc,clear,close all
prob=optimproblem();
x=optimvar("x",6,1,"LowerBound",0);
q=[0.025,0.015,0.055,0.026]';
b=[1,1.01,1.02,1.045,1.065];
c=[0.05,0.27,0.19,0.185,0.185];
M=10000;
prob.Objective=x(6);
prob.Constraints.con1=q.*x(2:5)<=x(6);
prob.Constraints.con2=b*x(1:5)==M;
k=0;kk=[];vv=[];xx=[];
hold on
while k<0.26
prob.Constraints.con3=c*x(1:5)>=k*M;
%k取太大可能造成无解,则k没有对应的v,plot会报错
[s,v]=solve(prob);
kk=[kk;k];
vv=[vv;v];
xx=[xx;s.x'];
k=k+0.001;
end
plot(kk,vv,"*r");
xlabel("$k$","Interpreter","latex");
ylabel("$v$","Interpreter","latex","Rotation",0);
disp(kk);
disp(vv);
disp(xx);
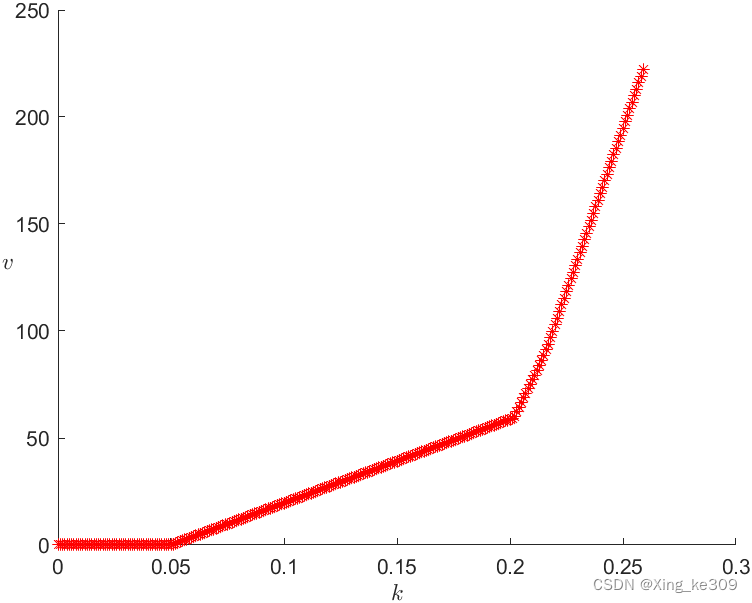
?由图和可得出与
相同的结论
对于拐点选择附近的,再缩小范围,可得出近似拐点
所以得当时,净收益为
,
?B:
???????????????????????
????????????????????????
clc,clear,close all
b=[1,1.01,1.02,1.045,1.065];
q=[0.025,0.015,0.055,0.026]';
c=[0.05,0.27,0.19,0.185,0.185];%ri-pi
M=10000;
prob=optimproblem();
x=optimvar("x",6,1,"LowerBound",0);
prob.Constraints.con1=b*x(1:5)==M;
prob.Constraints.con2=q.*x(2:5)<=x(6);
w=0.6;ww=[];tt=[];zz=[];xx=[];
while w<1
prob.Objective=w*x(6)-(1-w)*c*x(1:5);
[s,v]=solve(prob);
ww=[ww;w];
xx=[xx;s.x'];
t=s.x(6);
tt=[tt;t];%记录风险
z=c*s.x(1:5);
zz=[zz;z];%记录净收益
w=w+0.001;
end
subplot(3,1,1);
plot(ww,tt,"-r");
subplot(3,1,2);
plot(ww,zz,"-r");
subplot(3,1,3);
plot(tt,zz,"-r");
disp(ww);
disp(tt);
disp(zz);
disp(xx);
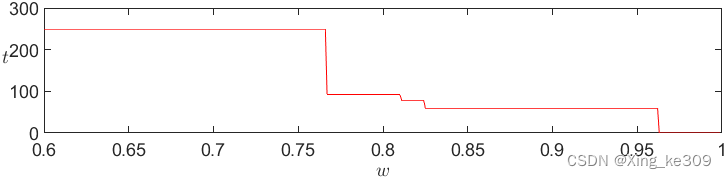
?
?
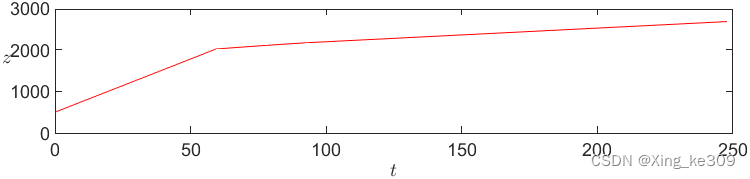
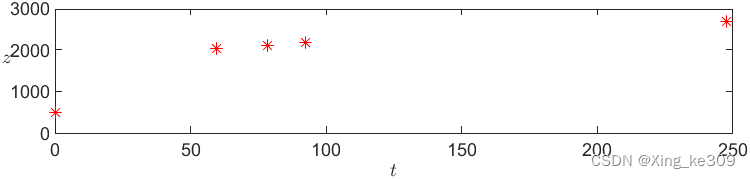
得到对应拐点的数据?
在拐点之前,风险与收益均平稳增涨,而后风险增幅变大,收益增幅相对减少。
所以选拐点处最合适,净收益为,
由前两张图和也可以得出和
同样的结论
小计:
- 多目标问题转换为线性归还求解
- 最大值最小化目标函数转化
- 图像与数据分析,拐点的特殊性
中循环的应用
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!