八大算法排序@冒泡排序

冒泡排序

概念

??冒泡排序（Bubble Sort）是一种简单直观的排序算法，它重复地遍历待排序序列，一次比较两个相邻的元素，如果它们的顺序错误就将它们交换过来。通过多次的遍历，使得最大的元素逐渐移动到待排序序列的最后，从而实现排序。

算法思想

??主要思路就是比较两个相邻的元素大小，如果顺序错误（与要实现的排序对比而言），则将两个元素交换位置。迭代比对下去，比完一趟后，实现最大的数移动到最后（升序）或最小的数移动到最后（降序），将数组的序列长度减1。
??按照以上的步骤，进行多趟的排序，最终实现数组的排序。我们那实现升序的一趟冒泡排序来进行模拟演变。

示例

如下是数组arr1 = { 6 , 4 , 3 , 9 , 2 , 1 , 5 , 7 , 8 }初始状态下的图文演示：

变量i存放未排序的第一个元素下标，end存放着数组的个数，数组最后一个元素的下标为end-1。

第一步：

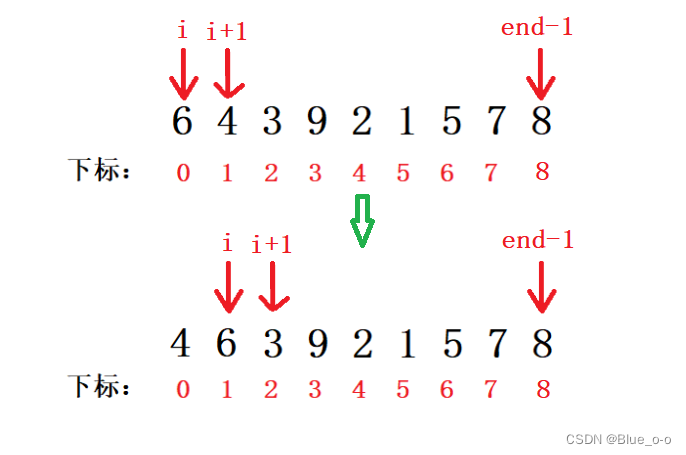
比较下标 i 和 i+1 相邻两个元素的大小。arr1[i] < arr[i+1]。交换元素的顺序，然后对变量 i 自加1，迭代下去进行下一对的比较。

第二步：

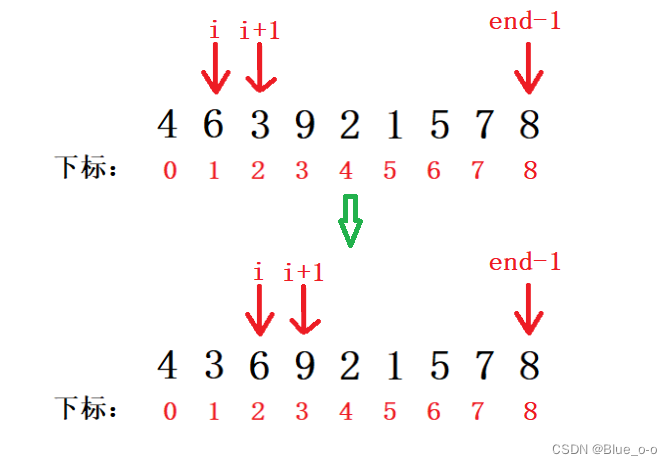
比较下标 i 和 i+1 相邻两个元素的大小。arr1[i] < arr[i+1]。交换元素的顺序，然后变量 i 自加1，迭代下去进行下一对的比较。

迭代过程就是重复以上的动作。下面是后序的全部过程，如下：

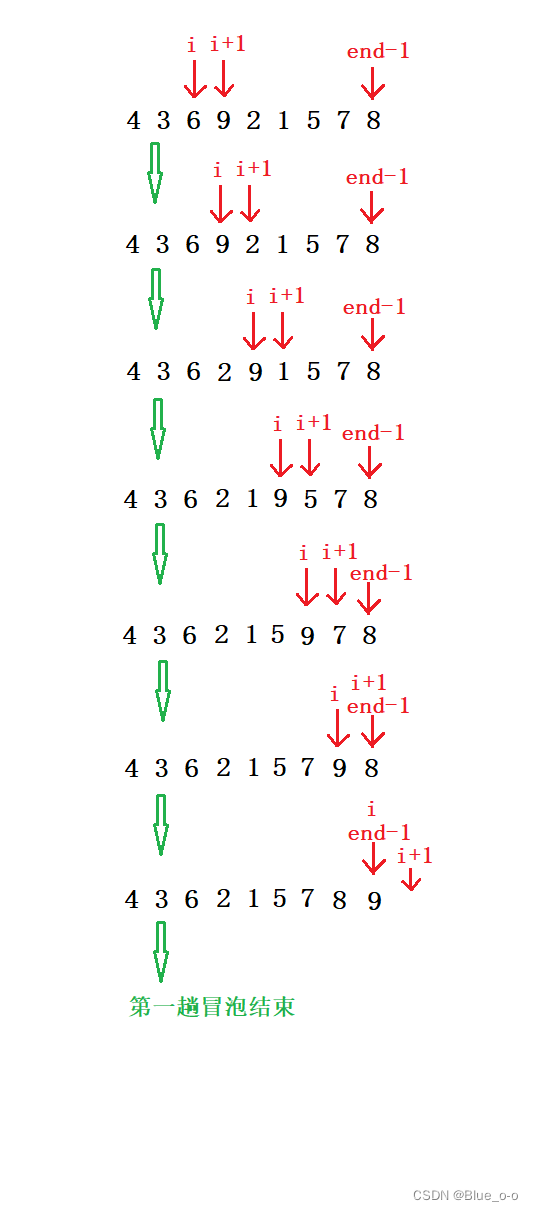
??第一趟冒泡排序完后，数组中最大的元素9已经被移动到最后，此时对end减1。end从原来的9变为了8。end-1 “指向” 的是下标7。此时可以数组划分为了两个序列，一个是排好序的（下标为8的元素）；另一个序列式未排好序的（下标为0 ~ 7的元素）。
（整个数组分为两个序列，前序列是未排好序的，后序列是排好序的。）

一趟冒泡排序排好一个元素，数组中还剩8个未排序的元素，那么只需要再执行七趟冒泡排序，最后当变量 i + 1 等于 end-1 时，判断是否交换arr1[i] 和 arr[i+1]，然后整个数组排序完成。最后一个不用排，肯定就是在最左端。

算法实现

// 冒泡排序
void BubbleSort(int* a, int n)
{
	// 实现代码1
	int end = n;
	// 执行n-1趟冒泡排序
	while (end-1)
	{
		// 一趟冒泡排序的实现
		for (int i = 0; i < end - 1; i++)
		{
			if (a[i] > a[i + 1])
			{
				Swap(&a[i], &a[i + 1]);
			}
		}
		end--;
	}

	 实现代码2
	//for (int i = 0; i < n-1; i++)
	//{
	//	for (int j = 0; j < n - 1 -i; j++)
	//	{
	//		if (a[j] > a[j + 1])
	//		{
	//			Swap(&a[j], &a[j + 1]);
	//		}
	//	}
	//}

}

时间复杂度

O(N^2)。

计算过程为：

（考虑最坏的情况，如对逆序的数组进行升序的排序）
移动第一个元素时，需要挪动n-1次；
移动第二个元素时，需要挪动n-2次；
...
移动第n-1个元素时，需要挪动1次；
移动第n个元素时，需要挪动0次。

挪动的次数是一个公差为1的等差数列，对该数列求和，根据等差数列的前n项和公式求得
Sn=n^2/2;
即时间复杂度为O(n^2/2)，又因为时间复杂度不计入系数的。
所以时间复杂度为O(n^2)。

空间复杂度

O(1)。

因为是在原数组上进行排序的，没有用到多余的空间，所以空间复杂度为O(1)。

特性总结

1、 冒泡排序是一种非常容易理解的排序
2.、时间复杂度：O(N^2)
3.、空间复杂度：O(1)
4.、稳定性：稳定